4.3. Оптимум потребителя: ординалистская концепция

С точки зрения ординалистской концепции, измерение полезности при помощи абсолютной шкалы (у кардиналистов) менее достоверно по сравнению с относительной шкалой, принятой в их теории. Для моделирования потребительского спроса используются кривые безразличия, показывающие предпочтения потребителя и бюджетное ограничение. Предпочтения потребителя касаются многих благ, однако в целях упрощения рассматриваются обычно два блага – X и Y.

Подход с позиции кривых безразличия предполагает не количественное соизмерение потребностей, а лишь их ранжирование. Кривая безразличия U – это множество точек, каждая из которых представляет собой такой набор из двух товаров, когда потребителю безразлично, какой из этих наборов выбрать, поскольку их полезность одинакова. Кривые безразличия могут быть проведены через любую точку пространства совокупности товаров, однако при этом они всегда имеют отрицательный наклон и никогда не пересекаются. Набор кривых безразличия, в котором каждая последующая кривая располагается выше и правее предыдущей, называется картой кривых безразличия (рис. 6.2). Более удаленные от начала координат кривые безразличия соответствуют более высоким уровням полезности.

К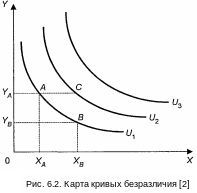 ривая безразличия U₁ графически отображает набор из товаров X и Y, который обладает одинаковой полезностью для потребителя (рис. 6.2). Допустим, что благо X является молоком, а благо Y – хлебом. Представим, что потребителю все равно – съесть 2 батона хлеба и запить его одним пакетом молока (точка А) или съесть 1 батон хлеба, запив его двумя пакетами молока (точка В). Кривая безразличия U₁ представляет все множество комбинаций хлеба и молока, имеющих одинаковую, с точки зрения потребителя, полезность. Чем правее и выше расположена кривая безразличия (U₂ или U₃), тем большее удовлетворение приносят представленные ею комбинации двух благ. Любой набор, лежащий на кривой безразличия U₂, предпочтительнее любого набора на кривой безразличия U₁, а набор, лежащий на кривой безразличия U₃, будет предпочтительнее набора на кривой безразличия U₂.

На кривой безразличия имеется участок, на котором возможна эффективная замена одного блага другим. Этот участок называется зоной замещения, или зоной субституции (отрезок АВ на рис. 6.3). Взаимная замена благ X и Y имеет смысл только в зоне субституции. Количество Y₁ – это минимально необходимое потребление блага Y, от которого потребитель не может отказаться, какое бы количество блага X ни предлагалось взамен. Также количество X₂ – это минимально необходимое потребление блага X, от которого потребитель не может отказаться, какое бы количество блага Y ни предлагалось взамен.

Рис. 6.3. Зона субституции и предельная норма замещения [2]

При определении пропорций замены одного блага другим используется понятие предельной нормы замены (замещения) MRS (от англ. marginal rate of substitution). Предельной нормой замещения благом X блага Y (MRS_XY) называется количество блага Y, на которое должно быть сокращено его потребление «в обмен» на увеличение количества блага X на единицу, с тем, чтобы уровень удовлетворения потребителя остался неизменным (рис. 6.3). Отрицательный наклон кривой безразличия означает, что потребитель, увеличивая объем потребления товара X на ΔX, должен отказаться от некоторого количества ΔY с тем, чтобы сохранить уровень полезности прежним. Отношение количества единиц блага Y к количеству единиц блага X (ΔY / ΔX) характеризует предельную норму замещения благом X блага Y:

MRS_XY = –ΔY / ΔX.

Поскольку –ΔY / ΔX, по определению, отрицательно, то минус перед дробью делает значение нормы замещения положительным. Увеличение полезности от потребления одного товара должно уравновесить снижение полезности от потребления другого товара.

Предельная норма замещения может принимать различные значения: MRS_XY = 0; MRS_XY = const (для двух взаимозаменяемых товаров); MRS_XY изменяется при движении вдоль кривой безразличия.

Кривые безразличия позволяют выявить потребительские предпочтения, но не учитывают два важных обстоятельства: каковы цены товаров и каков доход потребителя. Кривые безразличия показывают возможности замены одного блага другим, но не определяют, какой именно набор товаров потребитель считает для себя наиболее выгодным. Для изображения множества доступных потребителю товарных наборов используется бюджетная линия или бюджетное ограничение (линия цен и расходов). Она показывает, какие потребительские наборы можно приобрести за данную сумму денег (дохода). Если I – доход потребителя, PX – цена товара X, P_Y – цена товара Y, а X и Y – соответственно купленное количество товаров, то уравнение бюджетного ограничения будет иметь вид:

I = P_XX + P_YY.

Сущность бюджетного ограничения состоит в том, что доход потребителя равен сумме расходов на покупку товаров X и Y. Если потребитель весь доход I израсходует на покупку товара X, то он сможет приобрести его в количестве I/P_X. Если весь доход пойдет на приобретение товара Y, то потребитель купит его в количестве I/P_Y (рис. 6.4).

I/Р_y

Рис. 6.4. Бюджетное ограничение (бюджетная линия) [2]

Уравнение бюджетной линии (линии цен) для товаров X и Y примет вид:

Y = I/P_Y – (P_X/P_Y) X и X = I/P_X – (P_Y/P_X) Y.

Все товарные наборы, соответствующие точкам на бюджетной линии, по стоимости равны доходу I и поэтому доступны для потребителя. Все наборы, расположенные выше и правее бюджетной линии, стоят дороже и поэтому недоступны для потребителя. Таким образом, бюджетная линия ограничивает сверху множество желаемых для потребителя наборов.

Соединим на одном графике кривые безразличия и бюджетную линию. Точка касания кривой безразличия с бюджетным ограничением означает положение равновесия потребителя (рис. 6.5).

Рис. 6.5. Положение равновесия потребителя (оптимум потребителя) [2]

Потребитель не выберет точки A и B, в которых бюджетная линия пересекает кривую безразличия U₁, поскольку они расположены на более низкой кривой безразличия. Потребитель выберет точку E, в которой бюджетная линия касается кривой безразличия U₂, расположенной выше кривой U₁. При этом оптимальный для потребителя товарный набор E содержит X_E единиц товара X и Y_E единиц товара Y.

В точке E углы наклона кривой безразличия и бюджетной линии совпадают (наклон бюджетной линии: P_X / P_Y, наклон кривой безразличия: MRS_XY). Поэтому при данных ценах и доходе потребителя в точке оптимума выполняется равенство:

MRS_XY = P_X / P_Y.

Увеличение денежного дохода потребителя означает смещение бюджетной линии вправо вверх и переход потребителя на более высокую кривую безразличия. Аналогичная ситуация может возникнуть при снижении цен обоих товаров, что соответствует увеличению реального дохода. При уменьшении денежного дохода или росте цен бюджетная линия сдвигается влево вниз.

ТЕМА 5. ТЕОРИЯ ПРОИЗВОДСТВА ЭКОНОМИЧЕСКИХ БЛАГ

5.1. Основы производства товара: производственная функция.

5.2. Производство в краткосрочном периоде: закон убывающей предельной производительности.

5.3. Производство в долгосрочном периоде: отдача от масштаба.

Рекомендуемая литература: [1, гл. 9], [2, гл. 7], [3, гл. 10], [4, гл. 6], [5, гл. 5].

5.1. Основы производства товара: производственная функция

Теория производства изучает соотношение между количеством применяемых фирмой ресурсов и объемом выпуска товара. Методологически теория производства схожа с теорией потребления, однако ее основные категории имеют не субъективно-психологическую основу, а объективную природу и могут быть измерены в определенных единицах.

Основным инструментом экономического анализа производства является производственная функция, которая показывает зависимость количества продукта, производимого фирмой, от количества затраченных ресурсов. Производственной функции присущи общие свойства функции полезности блага в теории потребления, и это объясняется тем, что по отношению к ресурсам фирма является потребителем (покупателем экономических ресурсов).

Производственная функция описывает множество технически эффективных способов производства (технологий). Каждая технология характеризуется определенной комбинацией ресурсов, необходимых для получения одного и того же объема выпуска. При этом следует различать техническую и экономическую эффективность способа производства. Техническая эффективность – это максимально возможный объем производства, достигаемый в результате использования имеющихся ресурсов. Экономическая эффективность – это производство данного объема продукции с минимальными издержками.

В теории производства традиционно используется 2-факторная производственная функция, в которой объем производства является функцией использованных ресурсов труда L (от англ. labor) и капитала K (от англ. capital): Q = f (K, L). Графически каждый способ производства (технология) может быть представлен точкой, характеризующей минимальный необходимый набор двух факторов, нужных для производства данного объема продукции (рис. 7.1).

Рис. 7.1. Технология и производственная функция (изокванта) [5]

На графике показаны различные технологии производства товара: T₁, T₂, T₃. Они характеризуются разными соотношениями в применении труда L и капитала K: T₁ = L₁K₁; T₂ = L₂K₂; T₃ = L₃K₃. Наклон луча показывает размеры применения двух ресурсов – труда и капитала. Чем выше угол наклона луча, тем больше затраты капитала и меньше затраты труда. Например, технология T₁ наиболее капиталоёмка по сравнению с технологией T₂.

Линия на графике, показывающая разные сочетания производственных ресурсов и данный объем выпуска Q, называется изоквантой (от англ. isoquant), или линией равного выпуска. Изокванты для процесса производства означают то же, что и кривые безразличия для процесса потребления. Они обладают аналогичными свойствами: имеют отрицательный наклон, выпуклы относительно начала координат и не пересекаются друг с другом.

Объем производства Q может быть достигнут при разных комбинациях факторов производства K и L. Верхняя часть изокванты отражает капиталоемкие технологии, а нижняя – трудоемкие технологии. Выпуклость изокванты связана с взаимозаменяемостью ресурсов. Когда ресурсы являются взаимодополняемыми (комплементы), то изокванта имеет L-образную форму. Когда ресурсы являются взаимозаменяемыми (субституты) изокванта принимает форму прямой линии. Изокванты отражают альтернативные варианты затрат ресурсов (факторов производства) для производства определенного объема продукции. Совокупность изоквант, отражающая максимально достижимый выпуск продукции при любом заданном наборе факторов производства, называется картой изоквант. Чем дальше от начала координат располагается изокванта, тем больше объем выпуска товара (Q₁, Q₂, Q₃ на рис. 7.1).

При переходе из одной точки изокванты в другую происходит уменьшение затрат одного ресурса K с одновременным увеличением затрат другого ресурса L, но при этом выпуск продукции остается постоянным (Q = const), т. е. имеет место замещение одного ресурса (капитала) другим (трудом). Наклон изоквант характеризует предельную норму технического замещения MRTS (от англ. marginal rate of technical substitution) одного ресурса другим:

MRTS_LK = –ΔK / ΔL,

где –ΔK – изменение (уменьшение) затрат капитала; ΔL – изменение (увеличение) затрат труда.

С увеличением затрат труда от L₁ до L₂ уменьшаются затраты капитала от K₁ до K₂ (рис. 7.1). Это означает, что уменьшается предельная производительность труда MP_L (от англ. marginal product of labor)) и увеличивается предельная производительность капитала MP_K (от англ. marginal product of capital). В результате формула нормы технической замены (замещения) примет вид:

MRTS_LK = –ΔK / ΔL = –MP_L / MP_K.

С увеличением применения труда на ∆L выпуск продукции возрастет на ∆L × MP_L, а уменьшение применения капитала на –∆K сократит объем выпуска на –∆K × MP_K. Следовательно, увеличение количества применяемого труда полностью компенсирует сокращение применения капитала, если выполняется равенство:

∆L × MP_L = –∆K × MP_K.

Уменьшение предельной нормы технического замещения одного фактора другим (в данном случае замещение капитала трудом) свидетельствует о том, что эффективность использования любого ресурса ограничена. По мере замены капитала трудом отдача последнего (производительность труда) снижается. Аналогичная ситуация происходит и в результате замены труда капиталом. Это означает, что –∆L × MP_L + ∆K × MP_K = 0.

Изокванты показывают равные объемы выпуска при разных сочетаниях используемых ресурсов, но для производителя важно знать, как выбрать такое сочетание ресурсов, чтобы достичь максимального объема выпуска товара при минимальных издержках. В этом случае будет достигнут оптимум производителя (по аналогии с оптимумом потребителя), поскольку цель производителя товара – достичь максимального выпуска при данных затратах на приобретение ресурсов.

В теории производства оптимум производителя определяется равенством предельной нормы технического замещения одним ресурсом другого и соотношением их цен:

MRTS_LK = W / r = MP_L / MP_K или MP_L / W = MP_K / r.

Это означает, что оптимум производителя достигается тогда, когда последняя денежная единица, затраченная на труд, дает тот же прирост выпуска, что и последняя денежная единица, израсходованная на капитал.

Общие затраты фирмы на труд и капитал отражаются уравнением бюджетного ограничения производителя, которое имеет вид:

C = W L + r K,

где W – заработная плата как цена труда; r – ставка процента как цена капитала.

Из уравнения бюджетного ограничения выводится уравнение равных затрат (изокоста) для капитала и труда:

K = c / r – (W / r) L и L = c / W – (r / W) K.

Уравнение равных затрат (прямая линия MN на рис. 7.2) представляет комбинацию ресурсов (труда и капитала), использование которых ведет к одинаковым затратам, израсходованным на производство.

Рис. 7.2. Изокоста [5]

Рост бюджета производителя или снижение цен ресурсов сдвигает изокосту вправо (в положение M′N′), а сокращение бюджета или рост цен – влево (в положение M″N″).

Касание изокванты с изокостой определяет положение равновесия производителя, поскольку позволяет достичь максимального объема производства при имеющихся ограниченных средствах, которые можно затратить на покупку ресурсов (рис. 7.3). Учитывая, что в точке E изокванта и изокоста имеют одинаковый наклон, а наклон изокванты измеряется предельной нормой технического замещения, то условие равновесия производителя примет вид:

MRTS_LK = –ΔK / ΔL = –W / r.

Рис. 7.3. Равновесие производителя [5]

Если бюджет производителя товара возрастает, то он получает возможность выходить на изокванты более высокого уровня. Каждая точка касания будет показывать такую комбинацию факторов, которая соответствует минимуму затрат на производство данного объема продукции, обозначенного на изокванте. Соединение точек касания изокосты и изокванты покажет линию роста фирмы, которая получила название изоклиналь.