Решение.
Матрица смежности несимметричная, поэтому граф ориентированный. Количество вершин – 6. Строим граф. Из вершины 1 ведут дуги в вершины 2 и 3; из вершины 2 – в вершины 3 и 6; из вершины 3 – в вершину 4; из вершины 4 – в вершины 1, 5 и 6; из вершины 5 – в вершину 2; из вершины 6 – в вершину 1. Проверить правильность построения можно, посчитав полустепени исхода (сумма цифр по строке) и полустепени захода (сумма цифр по столбцу) для каждой вершины. Граф, соответствующий матрице смежности (табл. 5), изображен на рис. 5.
Рисунок 5 – Граф
Задание 5. По матрице инциденций (табл. 6) построить граф и определить, является ли он ориентированным или неориентированным.
Таблица 6 – Матрица инциденций графа
|
a |
b |
c |
d |
e |
f |
g |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
2 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
3 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
4 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
5 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
6 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
Решение.
В матрице инциденций нет значений (-1), потому можно сделать вывод о том, что граф неориентированный. Количество вершин равно 6, количество ребер – 7. Строим пустой граф на шести вершинах и соединяем их ребрами: ребро а соединяет вершины 1 и 4, ребро b – вершины 2 и 4, и т.д. Граф, соответствующий матрице инциденций (табл. 6), изображен на рис. 6.
Рисунок 5 – Граф
Задача 5. Определить, является ли
для графа
соответствующий маршрут цепью, простой
цепью, циклом, простым циклом, если
маршрут:
:
1)
;
2)
;
3)
;
4)
;
5)
.
Решение. Согласно определению получим:
1) простой цикл (все вершины и ребра различны);
2) цикл (все ребра различны, а вершины нет);
3) простая цепь;
4) маршрут (есть одинаковые ребра и вершины);
5) простая цепь.
Задание 6.
Для графов
и
на рисунке 6 выполнить операции
объединения, пересечения и композиции
и
.
Рисунок 6 – Графы и
Решение.
В графе
присутствуют все вершины и все дуги
графов
и
.
Так же, как в объединении множеств,
повторяющиеся элементы используем один
раз.
В графе
присутствуют те вершины и те дуги графов
и
,
которые есть и в графе
и в графе
.
На рисунке 7 изображены результаты
объединения и пересечения графов
и
.
Матрица смежности результирующего графа образуется поэлементным логическим сложением матриц смежности графов и .
Матрица смежности результирующего графа образуется поэлементным логическим умножением матриц смежности графов и .
Рисунок 7 – Объединение и пересечение графов и
Композиция графов
строится следующим образом: выписываются
все дуги
графа
и соответствующие им дуги
графа
,
в результирующий граф включаются дуги
,
исключая повторяющиеся (в данном случае,
дуга (1,3)):
-
(1,1)
(1,3)
(1,3)
(1,1)
(1,4)
(1,4)
(1,2)
(2,1)
(1,1)
(2,3)
(1,3)
(2,3)
–
(2,4)
(4,3)
(2,3)
(4,3)
–
Граф изображен на рис. 8. Матрица смежности графа получается умножением матрицы смежности графа на матрицу смежности графа .
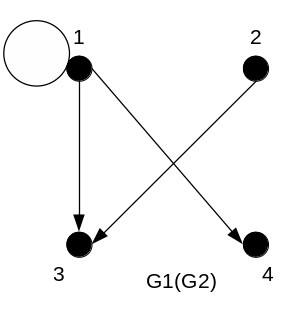
Рисунок 8 – Граф
Композиция графов строится следующим образом: выписываются все дуги графа и соответствующие им дуги графа , в результирующий граф включаются дуги :
-
(1,3)
–
(1,4)
(4,3)
(1,3)
(2,1)
(1,1)
(2,1)
(1,2)
(2,2)
(4,3)
–
Результирующий граф изображен на рис. 9. Матрица смежности графа получается умножением матрицы смежности графа на матрицу смежности графа .
Рисунок 9 – Граф
Операция композиции не является коммутативной, графы и не изоморфны.
Задача 1. Определить число компонент связности в графе , если задан следующим образом:
1)
2)
3)
Решение. 1) Граф имеет три компоненты
связности. В первую входят вершины
,
во вторую –
,
в третью –
,
так как вершины первой компоненты нельзя
соединить цепью с вершинами компонент
два и три, а вершины компонент два и три
также нельзя соединить цепью.
2) Граф имеет две компоненты связности,
в первую входят вершины
,
во вторую –
.
3) Граф имеет четыре компоненты связности.
В первую входят вершины
,
во вторую –
,
в третью –
,
в четвертую –
.
Задача 2. Найти в графе все точки сочленения и мосты, если :
Решение. Последовательно рассматриваем
ребра графа, мысленно удаляя их из графа,
только удаление ребра
приводит к увеличению числа компонент
связности, следовательно,
является мостом. Аналогично поступаем
с вершинами графа, и находим, что вершины
3 и 5 являются точками сочленения, так
как удаление их из графа приводит к
увеличению компонент связности.
Задача 3. Для графа
найти расстояние от точки
до всех вершин графа
, где
:
Решение. Расстояние от точки будем искать согласно алгоритма.
1.
,
2.
,
3.
,
просмотрели все вершины графа, отсюда
,
.
Задача 4. Найти расстояние от заданной
точки до заданной точки
и найти все геодезические цепи
,
если граф задан следующим образом:
Решение. 1.
,
2.
,
3.
,
4.
.
Следовательно,
.
Геодезические цепи
:
;
;
;
.
Задание 7. Найти Эйлерову цепь в неориентированном графе , изображенном на рис. 10.
Решение. Прежде, чем приступать к нахождению Эйлеровой цепи, необходимо проверить степени вершин графа − согласно утверждению, для существования Эйлеровой цепи, необходимо и достаточно, чтобы в графе ровно 2 вершины нечетной степени.
Рисунок 10.
В рассматриваемом
графе нечетные степени имеют вершины
и
(степень этих вершин равна 3). Соединяя
эти вершины фиктивным ребром так, как
показано на рис. 11, получаем граф
:
Рисунок 11.
Поскольку в
конечном итоге будет получена цепь, то
очевидно, что началом и концом этой цепи
будут вершины с нечетными степенями.
Поэтому, следуя описанному выше алгоритму,
будем циклы
так, чтобы хотя бы один из них начинался
или кончался на вершинах
или
.
Пусть цикл
составят ребра, проходящие через
следующие вершины:
.
Согласно алгоритму, удаляем из
все ребра, задействованные в цикле
.
Теперь граф
будет таким, как показано на рис. 12.
Составляем
следующий цикл
:
.
Граф
после удаления ребер, составляющих цикл
,
изображен на рис. 13.
|
|
|
|---|---|---|
Рисунок 12 |
Рисунок 13 |
|
Очевидно, что
последний цикл
будет состоять из v3 v5
v1|v3, где последнее
ребро, соединяющее вершины
и
– фиктивно. После удаления ребер,
составляющих цикл
,
в графе G не
останется ни одного ребра.
Теперь по общим
вершинам склеиваем полученные циклы.
Поскольку
и
имеют общую вершину
,
то, объединяя их, получим следующий
цикл:
.
Теперь склеим получившийся цикл с циклом
:
.
Удаляя фиктивное ребро, получаем искомую
Эйлерову цепь:
.
Задание 8. Установить изоморфность графов G1 и G2, приведенных на рис. 14.
Рисунок 14.
Запишем элементы
и
с соответствующими им парами и определим
частичную подстановку, проведя ребра
1 и 2, показанные на рис. 15. Затем
последовательно строим ребра 3-7, используя
отображения
и
и частичные подстановки. В результате
получаем подстановку
которая удовлетворяет
условию: для каждой вершины из
существует вершина из
,
для которой
и
и существует подстановка, переводящая
граф
в граф
.
Следовательно, графы
и
изоморфны.
Обобщенный алгоритм распознавания изоморфизма графов пригоден при решении большинства практических задач, за исключением тех случаев, когда рассматриваемые графы имеют одинаковое число вершин и все пары полустепеней исхода и захода каждой вершины одинаковы.
Рисунок 15.
Задание 9. Найти эксцентриситеты каждой вершины графа (рис. 16), радиус графа, его диаметр, центр, окружение и обхват.
Рисунок 16.
Решение. Эксцентриситет – наименьшее расстояние от вершины до наиболее удаленной от нее вершины графа. Диаметр – наибольший из эксцентриситетов, радиус – наименьший. Окружение – длина наименьшего простого цикла графа, обхват – длина наибольшего простого цикла. Центр находится в вершине (вершинах), на которых достигается минимальный эксцентриситет. Таким образом, для графа :
;
;
;
центр графа – вершина 4. Окружение, как
и обхват равны 3 (в графе всего один
цикл).
Задание_____. Найти в графе гамильтонов цикл.
Задание 11. В графе (рис. ____) найти компоненты сильной связности.
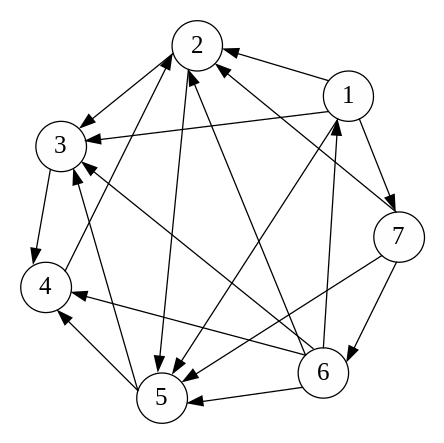
Рисунок ___.
Решение. Компонента сильной связности ориентированного графа – это
Задание 12. Найти хроматическое число графа (рис. ___).
Рисунок ___.
Решение. 1. Вычисляем степени всех вершин графа .
2. Просматриваем все вершины графа в порядке невозрастания степеней.
3. Окрашиваем в цвет №1 все неокрашенные вершины, не смежные с вершинами, уже окрашенными в цвет №1.
Рисунок ___.
4. Окрашиваем в цвет №2 все неокрашенные вершины, не смежные с вершинами, уже окрашенными в цвет №2.
Рисунок ___.
5. Окрашиваем в цвет №1 все неокрашенные вершины, не смежные с вершинами, уже окрашенными в цвет №1.
Рисунок ___.
Задание 13. Используя алгоритм Дейкстры, в графе найти кратчайшие расстояния от вершины 1 до всех остальных вершин.
Рисунок ___ – Граф
Решение. Строим
таблицу (см. лекции). На первом
шаге
присваиваем вершине 1 метку 0*,
а всем остальным вершинам –
.
.
|
|
|
|
|
|
|
|
|
|
1 |
0* |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
На втором шаге выписываем во второй столбец временные метки вершин (соответствующие весу дуги), в которые из 1-й вершины ведет дуга. Если дуги из вершины 1 нет, оставляем метку .
.
;
;
.
Из всех меток выбираем минимальную, записываем вершину с минимальной меткой в следующий столбец. В данном случае это вершина 2.
.
|
|
1 |
|
|
|
|
|
|
|
1 |
0* |
|
|
|
|
|
|
|
|
2 |
|
6* |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
4 |
|
7 |
|
|
|
|
|
|
|
5 |
|
7 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
Третий шаг: проделываем все операции для вершины 2:
.
;
;
.
Метки для остальных вершин оставляем прежними.
Из всех меток выбираем минимальную, записываем вершину с минимальной меткой в следующий столбец. В данном случае это вершина 3.
.
|
|
1 |
2 |
|
|
|
|
|
|
1 |
0* |
|
|
|
|
|
|
|
|
2 |
|
6* |
|
|
|
|
|
|
|
3 |
|
|
7* |
|
|
|
|
|
|
4 |
|
7 |
7 |
|
|
|
|
|
|
5 |
|
7 |
7 |
|
|
|
|
|
|
6 |
|
|
14 |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
Четвертый шаг: проделываем все операции для вершины 3:
.
;
.
Метки для остальных вершин оставляем прежними. Метка для вершины 6 уменьшилась. Записываем меньшую.
Из всех меток выбираем минимальную, записываем вершину с минимальной меткой в следующий столбец. В данном случае это вершина 4.
.
|
|
1 |
2 |
3 |
|
|
|
|
|
1 |
0* |
|
|
|
|
|
|
|
|
2 |
|
6* |
|
|
|
|
|
|
|
3 |
|
|
7* |
|
|
|
|
|
|
4 |
|
7 |
7 |
7* |
|
|
|
|
|
5 |
|
7 |
7 |
7 |
|
|
|
|
|
6 |
|
|
14 |
11 |
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
Пятый шаг: проделываем все операции для вершины 4:
.
;
.
Для вершины 2 расстояние не рассчитываем, т.к. она уже получила постоянную метку. Метки для остальных вершин оставляем прежними.
Из всех меток выбираем минимальную, записываем вершину с минимальной меткой в следующий столбец. В данном случае это вершина 5.
.
|
|
1 |
2 |
3 |
4 |
|
|
|
|
1 |
0* |
|
|
|
|
|
|
|
|
2 |
|
6* |
|
|
|
|
|
|
|
3 |
|
|
7* |
|
|
|
|
|
|
4 |
|
7 |
7 |
7* |
|
|
|
|
|
5 |
|
7 |
7 |
7 |
7* |
|
|
|
|
6 |
|
|
14 |
11 |
11 |
|
|
|
|
7 |
|
|
|
|
10 |
|
|
|
|
8 |
|
|
|
|
15 |
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
Шестой шаг: проделываем все операции для вершины 5:
.
;
;
;
;
Для вершины 4 расстояние не рассчитываем, т.к. она уже получила постоянную метку. Метки для остальных вершин оставляем прежними. Метки для вершин 6, 7, 8 уменьшились. Записываем меньшие.
Из всех меток выбираем минимальную, записываем вершину с минимальной меткой в следующий столбец. В данном случае это вершина 6.
.
|
|
1 |
2 |
3 |
4 |
5 |
|
|
|
1 |
0* |
|
|
|
|
|
|
|
|
2 |
|
6* |
|
|
|
|
|
|
|
3 |
|
|
7* |
|
|
|
|
|
|
4 |
|
7 |
7 |
7* |
|
|
|
|
|
5 |
|
7 |
7 |
7 |
7* |
|
|
|
|
6 |
|
|
14 |
11 |
11 |
9* |
|
|
|
7 |
|
|
|
|
10 |
9 |
|
|
|
8 |
|
|
|
|
15 |
11 |
|
|
|
9 |
|
|
|
|
|
16 |
|
|
|
Седьмой шаг: проделываем все операции для вершины 6:
.
;
Метки для остальных вершин оставляем прежними.
Из всех меток выбираем минимальную, записываем вершину с минимальной меткой в следующий столбец. В данном случае это вершина 7.
.
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
1 |
0* |
|
|
|
|
|
|
|
|
2 |
|
6* |
|
|
|
|
|
|
|
3 |
|
|
7* |
|
|
|
|
|
|
4 |
|
7 |
7 |
7* |
|
|
|
|
|
5 |
|
7 |
7 |
7 |
7* |
|
|
|
|
6 |
|
|
14 |
11 |
11 |
9* |
|
|
|
7 |
|
|
|
|
10 |
9 |
9* |
|
|
8 |
|
|
|
|
15 |
11 |
11 |
|
|
9 |
|
|
|
|
|
16 |
12 |
|
|
Восьмой шаг: проделываем все операции для вершины 7:
.
;
Метки для остальных вершин оставляем прежними.
Из всех меток выбираем минимальную, записываем вершину с минимальной меткой в следующий столбец. В данном случае это вершина 8.
.
Для вершины 9 метка на девятом шаге не меняется, поэтому все результаты записываем в таблицу.
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
1 |
0* |
|
|
|
|
|
|
|
|
2 |
|
6* |
|
|
|
|
|
|
|
3 |
|
|
7* |
|
|
|
|
|
|
4 |
|
7 |
7 |
7* |
|
|
|
|
|
5 |
|
7 |
7 |
7 |
7* |
|
|
|
|
6 |
|
|
14 |
11 |
11 |
9* |
|
|
|
7 |
|
|
|
|
10 |
9 |
9* |
|
|
8 |
|
|
|
|
15 |
11 |
11 |
11* |
|
9 |
|
|
|
|
|
16 |
12 |
12 |
12* |
Таким образом, минимальные расстояния от вершины 1 ко всем вершинам графа равны:
Задание 14. Найти максимальный поток в транспортной сети, изображенной на рисунке _____.
Рисунок ____.
Решение. Для нахождения максимального потока воспользуемся алгоритмом Форда-Фалкерсона. Найдем суммарную пропускную способность дуг, выходящих из истока (вершина 1) и суммарную пропускную способность дуг, входящих в сток (вершина 14).
;
.
Значит, максимальный поток в этой сети не может превосходить 31.
Далее разбиваем сеть на простые непересекающиеся цепи (произвольным образом). В данном случае удобно сделать это следующим образом:
1 – (1, 2, 6, 10, 14);
2 – (1, 3, 7, 11, 14);
3 – (1, 4, 8, 12, 14);
4 – (1, 5, 9, 13, 14).
Для каждой из цепей находим максимальный поток, исходя из пропускных способностей дуг: например, в первой цепи – (1, 2, 6, 10, 14) – минимальная пропускная способность у дуги (2,6) – 6, поэтому поток по этой дуге не может превышать 6-ти.
На рис. _____ показана сеть, в которой синим цветом обозначены простые цепи, а рядом с пропускными способностями дуг обозначено значение потока. Дуги, у которых пропускная способность равна потоку, называются насыщенными.
На первой итерации получаем суммарный поток: 6+5+6+4=21.
На следующих итерациях будем пытаться увеличить величину потока.
Рисунок ____ – первая итерация.
Для этого выбираем другие цепи, в которых нет насыщенных дуг.
На рисунках _______ изображены последующие итерации. (Над дугой рядом с пропускными способностями дуг через «;» обозначаем новое значение потока).
Вторая итерация: выбираем цепь, по которой можно увеличить поток: (1, 2, 3, 6, 10, 14). Поток можно увеличить на 1 (т.к. пропускная способность дуги (6, 10) равна 7).
Рисунок ____ – вторая итерация.
На второй итерации поток увеличился на 1, и стал равен 22.
Третья итерация: выбираем цепь (1, 3, 8, 7, 10, 14). По этой дуге мы можем пропустить поток величиной 2 (т.к. пропускная способность дуги (3,8) равна 2). Получаем суммарный поток, равный 22+2=24. На рис. ____ изображена сеть с потоком, равным 24.
Рисунок ____ – третья итерация.
Четвертая итерация: выбираем цепь (1, 4, 9, 13, 14). По этой дуге мы можем пропустить поток величиной 1 (т.к. пропускная способность дуги (9, 13) равна 5). Получаем суммарный поток, равный 24+1=25. На рис. ____ изображена сеть с потоком, равным 25.
Рисунок ____ – четвертая итерация.
Задание 9.
Доказать справедливость соотношения
.