`Практика Примеры решения типовых задач
Задание 1.
Определить
степени каждой вершины графа
на рис. 1. Построить его дополнение.
Рисунок 1 – Граф
Решение. Степени
вершин определяются количеством ребер,
ей инцидентных. Поэтому:
;
;
;
;
;
.
Дополнение графа
строится следующим образом: из полного
графа на 6-ти вершинах
убираются те ребра, которые принадлежат
графу
.
На рис. 2 ребра графа
отмечены пунктиром.
Рисунок 2 – Граф
Рисунок 3 – Дополнение графа
Проверить правильность построения можно так: Сумма степеней одноименных вершин графа и его дополнения равна 5 (степень вершины графа ).
Задание 2. Построить матрицы смежности и инциденций для неориентированного графа на рис.4.
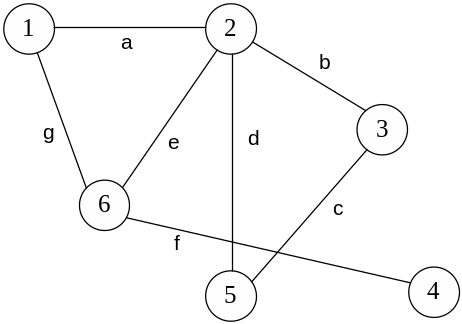
Рисунок 4 – Граф
Решение.
Строим матрицу
смежности
,
строки и столбцы которой обозначаем
вершинами графа. Для неориентированного
графа она симметричная. Элемент
матрицы смежности
равен 1, если вершины
и
смежны, и 0 в противном случае. Так как
граф
простой (не имеет петель и кратных
ребер), на главной диагонали расположены
0, а все элементы матрицы имеют значения
0 или 1. Сумма чисел по строке (и по столбцу)
равна степени вершины.
Таблица 1 – Матрица смежности неориентированного графа
-
1
2
3
4
5
6
1
0
1
0
0
0
1
2
1
0
1
0
1
1
3
0
1
0
0
1
0
4
0
0
0
0
0
1
5
0
1
1
0
0
0
6
1
1
0
1
0
0
Матрица инциденций
строится следующим образом: строки ее
соответствуют вершинам, столбцы –
ребрам графа
.
Элемент
равен 1, если вершина инцидентна ребру,
и 0 – в противном случае.
Таблица 2 – Матрица инциденций неориентированного графа
|
a |
b |
c |
d |
e |
f |
g |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
2 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
3 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
4 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
5 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
6 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
В каждом столбце должны находиться только 2 единицы. Сумма чисел по строке равна степени вершины.
Задание 3. Построить матрицы смежности и инциденций для ориентированного графа на рис. 5.
Рисунок 5 – Граф