Дополнение графа
Определение.
Дополнением
графа
с
вершинами называется граф
,
который содержит все вершины графа
и те ребра, которые принадлежат полному
графу
,
но не принадлежат графу
,
т.е.
.
Пример. На рисунке 6.20 изображен граф и его дополнение.
Рисунок 6.20 – Граф и его дополнение
Объединение графов
Определение.
Объединением
графов
и
называют
граф такой, что
Объединение
графов
и
называется
дизъюнктным,
если
.
Операция объединения обладает следующими свойствами, которые следуют из определения операции и свойств операций на множествах:
1.
– свойство коммутативности;
2.
– свойство ассоциативности.
Операция объединения графов может быть выполнена в матричной форме. Для графов с одним и тем же множеством вершин справедлива следующая теорема.
Теорема
6.3.
Пусть
и
– два графа (ориентированные или не
ориентированные одновременно) с одним
и тем же множеством вершин
,
и пусть
и
– матрицы смежности вершин этих графов.
Тогда матрицей смежности вершин графа
является матрица
,
образованная поэлементным логическим
сложением матриц
и
.
Рисунок 6.21 – Объединение графов.
Рисунок 6.22 – Дизьюнктное объединение графов.
Пересечение графов
Определение.
Пусть
и
– произвольные графы. Пересечением
графов
и
называется граф с множеством вершин
с множеством ребер (дуг)
.
Операция пересечения обладает следующими свойствами, которые следуют из определения операции и свойств операций на множествах:
1.
–
свойство коммутативности;
2.
– свойство ассоциативности.
Для того чтобы операция пересечения была всеобъемлющей, необходимо ввести понятие пустого графа.
Определение.
Граф
называется пустым, если множество
вершин графа является пустым (
).
Заметим, что в этом случае и множество
ребер (дуг) графа также пустое множество
(
).
Пустой граф обозначается символом
.
Такой граф может быть получен в результате
выполнения операции пересечения графов,
у которых
.
В этом случае говорят о непересекающихся
графах.
Теорема
6.4.
и
– два графа (ориентированные или
неориентированные одновременно) с одним
и тем же множеством вершин
,
и пусть
и
– матрицы смежности вершин этих графов.
Тогда матрицей смежности вершин графа
является матрица
,
образованная поэлементным логическим
умножением матриц
и
.
Рисунок 6.23 – Пересечение графов.
Соединение графов
Определение.
Соединением
(сильным произведением) графов
и
(
)
называют граф такой, что
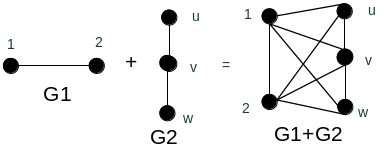
Рисунок 6.24 – Соединение графов
Композиция графов
Определение.
Пусть
и
– два графа с одним и тем же множеством
вершин
.
Композицией
графов
и
называется граф с множеством вершин
,
в котором существует дуга
тогда и только тогда, когда существует
дуга
,
принадлежащая множеству
,
и дуга
,
принадлежащая множеству
.
Пример. Рассмотрим выполнение операции композиции на графах, изображенных на рис. 6.25. Для рассмотрения операции составим таблицу, в первом столбце которой указываются ребра , принадлежащие графу , во втором — ребра , принадлежащие графу , а в третьем — результирующее ребро для графа .
Таблица 3 – Построение композиции графов
Заметим,
что дуга
результирующего графа в таблице
встречается дважды. Однако, поскольку
рассматриваются графы без параллельных
ребер (дуг), то в множестве E результирующего
графа дуга
учитывается только один раз, т.е.
.
На
рис. 6.25 изображены графы
и
и их композиция
.
На этом же рисунке изображен граф
.
Рекомендуется самостоятельно построить
граф
,
и убедиться, что графы
и
не изоморфны.
Рисунок 6.25 – Композиция графов