Список ребер

Определение. Список рёбер – это тип представления графа в памяти компьютерной программы, подразумевающий, что каждое ребро представляется двумя числами – номерами вершин этого ребра. Список рёбер более удобен для реализации различных алгоритмов на графах по сравнению с матрицей смежности.

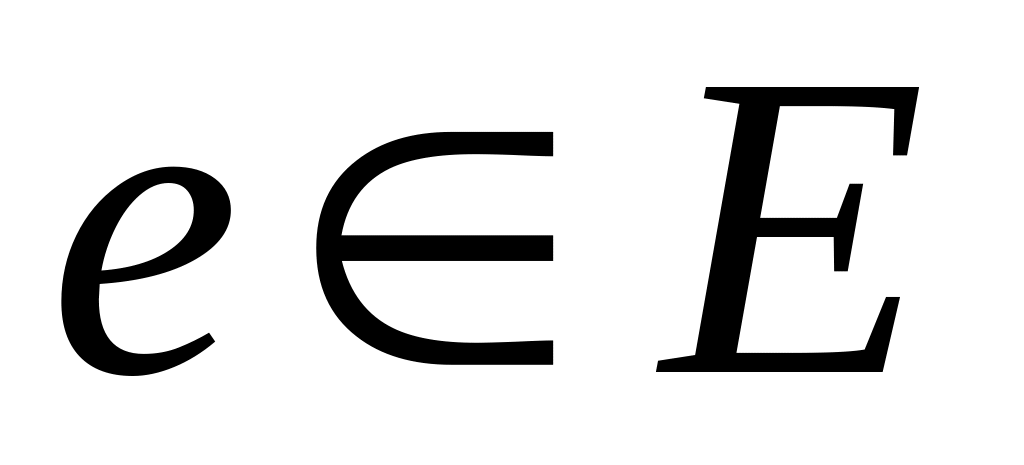
• Более абстрактно, граф можно задать как тройку , где и – некоторые множества (вершин и рёбер, соотв.), а – функция инцидентности, сопоставляющая каждому ребру (упорядоченную или неупорядоченную) пару вершин u и v из V (его концов).

На основе рассмотренных понятий можно дать окончательные определения неориентированного и ориентированного графов.

Назовем абстрактным неориентированным графом совокупность непустого множества , произвольного множества , причем , и произвольного отображения . Элементы множеств и – соответственно вершины и ребра графа, а – отображение инцидентности (отношение смежности).

Абстрактный ориентированный граф (орграф) представляет собой совокупность непустого множества , произвольного множества , причем такого, что , и произвольного отображения ; элементы множеств и являются соответственно вершинами и дугами графа , а – отображение инцидентности (отношение смежности).

Число вершин и ребер графа

Теорема 6.1. Сумма степеней вершин неориентированного графа равна удвоенному числу его ребер, т.е. если , то .

Это утверждение почти очевидно и следует из того, что каждое ребро графа инцидентно ровно двум вершинами, и поэтому вклад каждого ребра в сумму степеней вершин равен двум.

Теорема 6.2. В неориентированном графе число вершин нечетной степени четно.

Для доказательства этого утверждения разобьем множество вершин графа на два подмножества и , , причем и – соответственно множества вершин графа, имеющих четные и нечетные степени. С учетом теоремы 6.1 можно записать:

В правой части этого выражения – разность двух целых четных чисел, поэтому и должна быть величиной четной. Но это может быть только в том случае, если и четно.

Для ориентированного графа сумма полустепеней исхода равна сумме полустепеней захода и равна количеству ребер графа:

Операции над графами. Операции удаления ребер и вершин.

Удаление ребра. Пусть – ребро графа . Граф получается из графа в результате удаления ребра , т.е. .

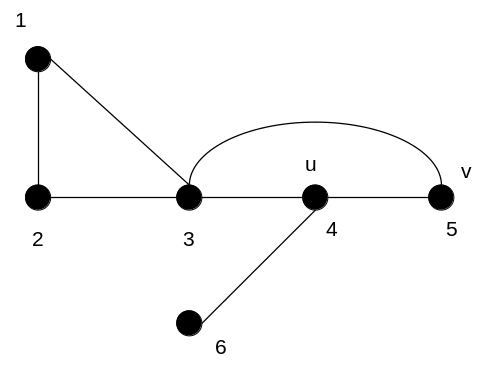
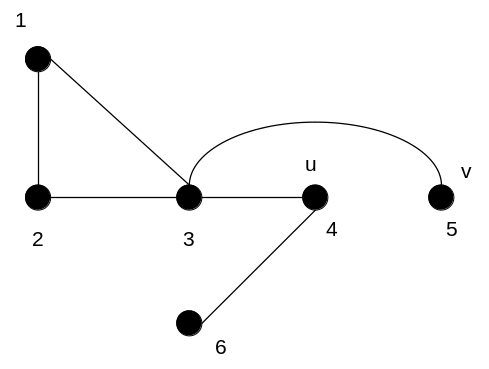
Рисунок 6.16 –Удаление ребра

Удаление вершины. Пусть – вершина графа . Граф получается из графа G в результате удаления вершины и всех инцидентных ей ребер, т.е. _.

Рисунок 6.17 –Удаление вершины .

Операция введения вершины в ребро и операция введения ребра в граф.

Операция введения вершины в ребро. Пусть и Операция введения вершины в ребро преобразует это ребро в два ребра и .

Рисунок 6.18 – Введение вершины.

Операция введения ребра в связный граф состоит в том, что в граф вводится ребро между двумя несмежными вершинами и . Эта операция выражается через операцию объединения графа и дерева Формально это записывается так:

.

Корректность такого представления следует из того, что объединение двух связных графов, имеющих общие вершины, будет связным графом. Ясно также, что справедливо тождество вида

.

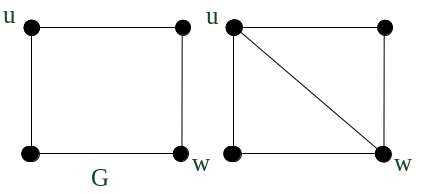
Рисунок 6.19 – Введение ребра.