Матрица смежности
Матрицу можно сделать квадратной для любого графа. В таких случаях строки и столбцы изображают вершины. На пересечении строк и столбцов ставится число, если соответствующие вершины соединены ребром (ребрами) и ставится число 0, если вершины не соединены.
Определение.
Матрица смежности
графа
с конечным числом вершин
(пронумерованных числами от 1 до
)
– это квадратная матрица
размера
,
в которой значение элемента
равно числу ребёр из
–й
вершины графа в
–ю
вершину.
Матрица смежности неориентированного графа является симметричной и не меняется при транспонировании. Хотя формально каждая вершина всегда смежная сама с собой, в матрице смежности мы будем ставить 0, если у нее нет петли, и 1, если есть одна петля. Если граф имеет матрицу смежности и не имеет петель, на главной диагонали у него всегда стоят нули. Элементы матрицы смежности определяются следующим образом:
Матрица смежности ориентированного графа не симметрична. Элементы ее определяются следующим образом:
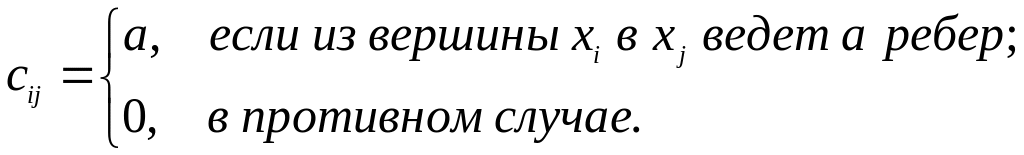
Пример. Построим матрицы смежности для графов на рисунке 6.15.
Таблица 1 – Матрица смежности ориентированного графа (рис. 6.15а)
|
1 |
2 |
3 |
4 |
5 |
6 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
0 |
1 |
0 |
0 |
0 |
0 |
4 |
0 |
1 |
0 |
0 |
1 |
0 |
5 |
1 |
0 |
0 |
0 |
0 |
1 |
6 |
0 |
0 |
1 |
0 |
0 |
0 |
Сумма элементов по строке равна степени полуисхода вершины, сумма элементов по столбцу – степени полузахода вершины.
Таблица 2 – Матрица смежности неориентированного графа (рис. 6.15б)
|
1 |
2 |
3 |
4 |
5 |
6 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
2 |
1 |
0 |
1 |
1 |
0 |
0 |
3 |
0 |
1 |
0 |
0 |
0 |
1 |
4 |
1 |
1 |
0 |
0 |
1 |
0 |
5 |
1 |
0 |
0 |
1 |
0 |
1 |
6 |
0 |
0 |
1 |
0 |
1 |
0 |
Сумма элементов по строке (и по столбцу) равна степени вершины.