Способы задания графов Геометрическая реализация графа
Человеку удобно работать с графом-рисунком, так как он может легко установить связь между вершинами в наглядном виде с помощью ребер, изображаемых непрерывными линиями. Такое геометрическое представление плоского графа называется его реализацией. При переходе от алгебраического способа к геометрическому одному и тому же графу могут соответствовать различные изображения – изоморфные графы, при этом от правильного изображения зависит, например, свойство плоской реализуемости. Для этого нужно правильно задать сам граф. Основным способом задания графа является перечисление всех его вершин и ребер. Но такое представление, во-первых, несимметрично (с ним трудно работать, особенно ЭВМ), во-вторых, для указания каждого ребра нужно еще раз выписывать соответствующие вершины, что плохо с точки зрения сжатия и хранения информации.
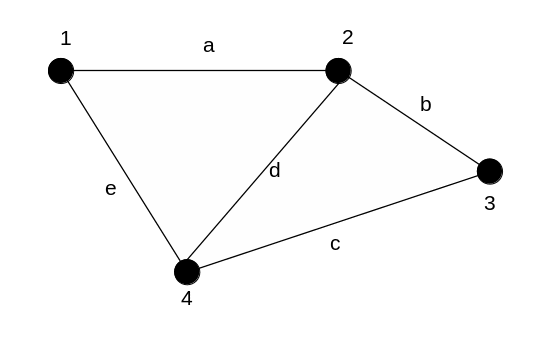
Рисунок 6.14 – Геометрический способ задания графа.
Матрица инциденций (инцидентности)
При
задании графа таблицей
составляется
таблица,
состоящей
из
строк
(вершины) и
столбцов
(ребра). На пересечении строк и столбцов
пишутся соответствующие знаки, которые
показывают отношение (инцидентность)
вершины и ребра. Это может быть знаки
“+” и “ – ”, числа 0,1, – 1 и др. Главным
во всех способах задания графа (диаграммой,
матрицей, таблицей) является указание
соответствия между множествами
вершин
к
ребер
.
Пусть
дан граф
,
где
– вершины,
а
– ребра,
среди которых могут и кратные ребра
(есть вершины, которые соединяет несколько
ребер).
Определение.
Матрицей инциденций
В
данного
графа будет таблица,
состоящая
из
строк (вершины) и
столбцов
(ребра). При рассмотрении неориентированного
графа на пересечении строк и столбцов
ставится число 1, если соответствующие
вершина и ребро инцидентны (
)
и ставится число 0, если они не
инцидентны. Элементы матрицы инциденций
неориентированного графа определяются
следующим образом:
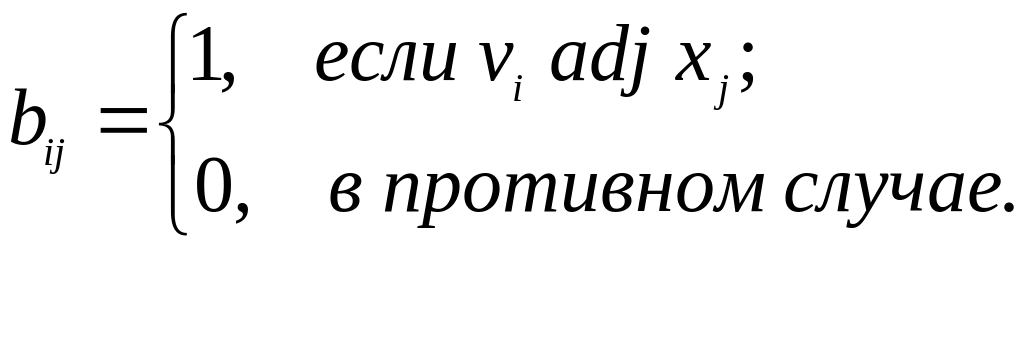
При рассмотрении ориентированного графа на пересечении строк и столбцов ставится число 1, если из вершины выходит соответствующее ее ребро. Если в вершину входит ребро, то ставят число (– 1). Если вершина не инцидентна ребру, то ставится число 0. Элементы матрицы инциденций неориентированного графа определяются следующим образом:
Очевидно, что в каждом столбце матрицы инцидентности должно быть только два ненулевых числа, так как ребро инцидентно двум вершинам. Число ненулевых элементов каждой строки – степень соответствующей вершины.
Матрицы инцидентности прямоугольные, если число строк и столбцов различно. Если число вершин и ребер в графе одинаковое, то получается квадратная матрица.
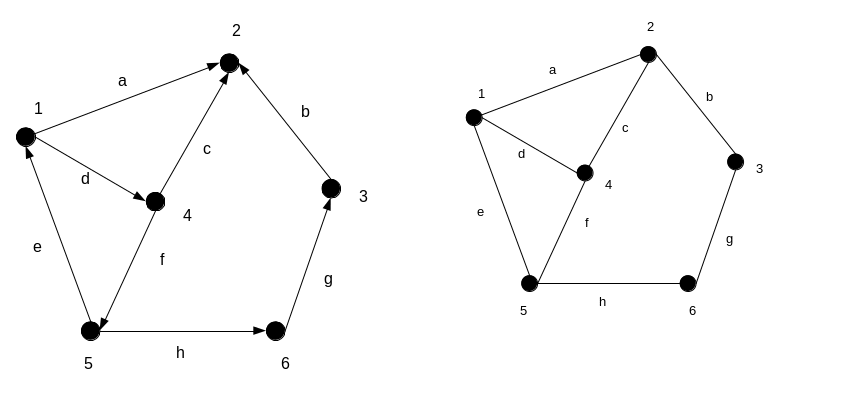
Рисунок 6.15 – Ориентированный и соответствующий ему неориентированный графы
Пример. Построим матрицы инциденций для графов на рисунке 6.15.
Таблица 1 – Матрица инциденций ориентированного графа (рис. 6.15а)
|
a |
b |
c |
d |
e |
f |
g |
h |
1 |
1 |
0 |
0 |
1 |
-1 |
0 |
0 |
0 |
2 |
-1 |
-1 |
-1 |
0 |
0 |
0 |
0 |
0 |
3 |
0 |
1 |
0 |
0 |
0 |
0 |
-1 |
0 |
4 |
0 |
0 |
1 |
-1 |
0 |
1 |
0 |
0 |
5 |
0 |
0 |
0 |
0 |
1 |
-1 |
0 |
1 |
6 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
-1 |
Таблица 2 – Матрица инциденций неориентированного графа (рис. 6.15б)
|
a |
b |
c |
d |
e |
f |
g |
h |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
3 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
4 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
5 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
6 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
Несложно заметить, что количество единиц в строке, соответствующей вершине, для ориентированных графов определяет полустепень исхода, количество (-1) – полустепень захода. Для неориентированных графов – просто степень вершины.