Теория Разновидности графов. Неориентированный граф. Определения.
Граф
или неориентированный
граф
– это
упорядоченная
пара
,
для которой выполнены следующие условия:
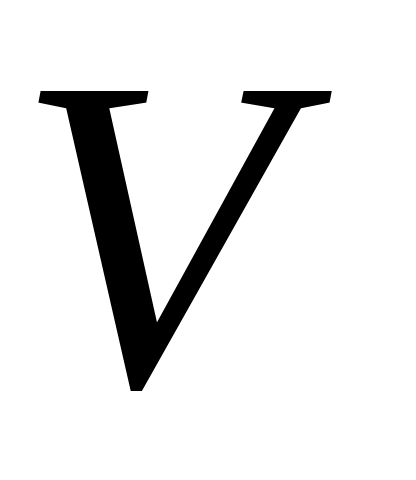это
непустое множество
вершин или узлов,
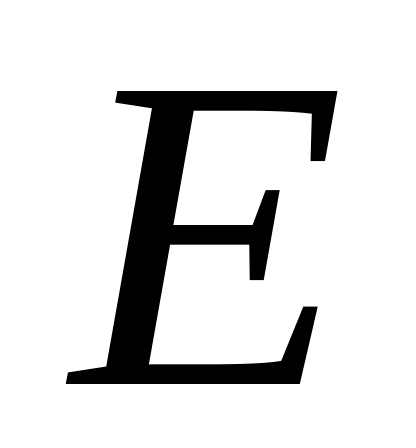это
множество пар (в случае неориентированного
графа – неупорядоченных) вершин,
называемых рёбрами.
(а значит и , иначе оно было бы мультимножеством) обычно считаются конечными множествами. Многие хорошие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов. Это происходит потому, что ряд соображений становится ложным в случае бесконечных множеств.
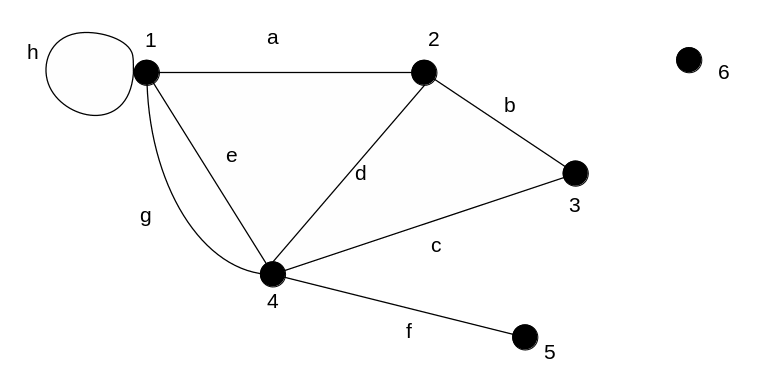
Рисунок 6.1 – Неориентированный граф
Вершины
и рёбра графа называются также элементами
графа, число вершин в графе
– порядком,
число рёбер
– размером
графа.
Вершины
и
называются концевыми
вершинами (или просто концами)
ребра
.
Ребро, в свою очередь, соединяет
эти вершины. Две концевые вершины одного
и того же ребра называются соседними
(смежными).
Два ребра называются смежными, если они имеют общую концевую вершину. Таким образом, на множествах вершин и ребер неориентированного графа могут быть заданы отношения смежности.
Вершина называется инцидентной ребру, если она является его концевой вершиной. Таким образом, на множествах вершин и ребер графа может быть задано отображение инцидентности.
Два ребра называются кратными, если множества их концевых вершин совпадают.
Ребро
называется петлёй,
если его концы совпадают, то есть
.
Степенью
(или
)
вершины
называют количество рёбер, для которых
она является концевой (при этом петли
считают дважды).
Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.
Пример.
На
рисунке 6.1 порядок графа
(количество вершин), размер графа
(количество ребер); 1 и 2 – смежные вершины
(их соединяет ребро
);
ребра
– смежны (имеют общую вершину 2); ребра
и
– кратные (соединяют вершины 1 и 4);
– петля; 5 – висячая вершина; 6 –
изолированная вершина. Степень вершины
2 –
,
степень вершины 4 –
,
степень вершины 1 –
(петля считается 2 раза).
Ориентированный граф. Определения.
Ориентированный
граф
(сокращённо орграф)
– это упорядоченная
пара
,
для которой выполнены следующие условия:
это непустое множество вершин или узлов,
это
множество (упорядоченных) пар различных
вершин, называемых дугами или
ориентированными рёбрами.
Дуга
– это
упорядоченная пара вершин
,
где вершину
называют началом, а
– концом дуги.
В
отличие от неориентированных графов,
в ориентированных степень вершины
определяется полустепенью
захода
и полустепенью
исхода:
соответственно,
и
.
Полустепень захода определяется
количеством ребер, концом которых
является данная вершина, полустепень
исхода – количеством ребер, началом
которых является вершина.
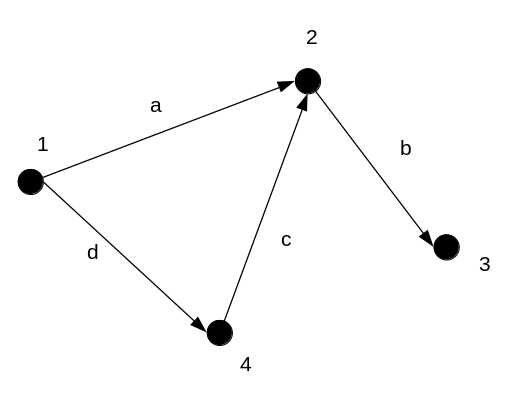
Рисунок 6.2 – Ориентированный граф
Пример. На рисунке 6.2 полустепени исхода и захода вершин:
