
- •Предмет и метод статистики
- •Статистичні графіки
- •3.Понятия и категории статистической науки.
- •9. Сведение и группировка статистических данных.
- •10. Статистическая таблица.
- •11. Статистические показатели: основные понятия и категории. Виды статистических показателей.
- •12. Относительные статистические показатели. Расчет относительных величин интенсивность и сравнение в пространстве.
- •13 Расчет относительных величин выполнения плана и планового задания, их связь с показателям динамики.
- •14. Расчет относительных величин динамики и координации.
- •15. Расчет относительных величин структуры и структурних сдвигов.
- •16. Середні статистичні показники . Розрахунок та застосування середньої, арифметичної простої ,зваженої
- •22. Мода. Расчет моды в дискретных и интервальных рядах распределения.
- •23. Медианна. Расчет мидианны в дискретных и интервальных рядах распределения.
- •24. Ряды распределения
- •24. Частотные статистические характеристики рядов распределения
- •25. Характеристики центра распределения.
- •26. Статистические характеристики вариации.
- •28. Графическое изображение рядов распределения
22. Мода. Расчет моды в дискретных и интервальных рядах распределения.
Мода – это варианта, имеющая наибольшую частоту, то есть значение признака, наиболее часто встречающееся в совокупности. В дискретном ряду (определяется визуально). Если моды две – то это бимодальный вариационный ряд
36,37,37,38,37,38,39,40 Мо=37
В интервальном ряду распределения сначала определяется модальный интервал, а уже в пределах этого интервала – точное значение моды.
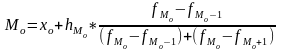
(где хо – нижня граница модального интервала; hMo – ширина модального интервала;
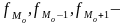 частота
модального, предмодального и послемодального
частота
модального, предмодального и послемодального
интервалов соответственно).
Определение моды по дискретному вариационному ряду: наибольшую частоту (60 человек) имеет 5-й тарифный разряд, следовательно, он и является модальным. Mo = 5.
23. Медианна. Расчет мидианны в дискретных и интервальных рядах распределения.
Медиана – значение признака, являющееся серединой вариационного ряда, то есть делящее его на две равные части.
36,37,37,37|38,38,39,40

В интервальном ряду распределения сначала определяется медианный интервал, а уже в пределах этого интервала – точное значение медианы:

де хо – нижня граница медианного интервала;
hMo
–
ширина
медианного
интервала;
 – частота медианного интервала;
– частота медианного интервала;
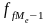 – кумулятивная
частота предмедианного интервала)
– кумулятивная
частота предмедианного интервала)
В
одномодальных симметричных рядах
распределения

Для
определения медианы в
дискретном ряду
при наличии частот сначала вычисляют
полусумму частот
![]() ,
а затем определяют, какое значение
варианта приходится на нее. (Если
отсортированный ряд содержит нечетное
число признаков, то номер медианы
вычисляют по формуле:
,
а затем определяют, какое значение
варианта приходится на нее. (Если
отсортированный ряд содержит нечетное
число признаков, то номер медианы
вычисляют по формуле:
Ме = (n(число признаков в совокупности) + 1)/2,
в случае четного числа признаков медиана будет равна средней из двух признаков находящихся в середине ряда
Если мода отражает наиболее распространенный вариант значения признака, то медиана практически выполняет функции средней для неоднородной, не подчиняющейся нормальному закону распределения совокупности.
24. Ряды распределения
Ряд распределения характеризует состав, структуру совокупности по определенному признаку. Элементами ряда распределения являются варианты – значения признака xj и частоты fj. В зависимости от статистической природы вариант ряды делятся на атрибутивные и вариационные. В соотношении вариант и частот проявляется закономерность распределения.
Построение рядов распределения выплывает из принципов статистического группирования. Известно, что ряды распределения можно образовать или по атрибутивным, или по количественным (вариационным) признакам.
При построении атрибутивных рядов распределения варианты нужно расположить в логической последовательности. В случае использования дискретных и интервальных вариационных рядов варианты записывают по возрастанию или убыванию. Для интервальных рядов важно четко разграничивать варианты.
Различают ряды распределения с абсолютными, относительными и накопленными частотами. Накопленные частоты называют кумулятивными. В первом случае частоты являются абсолютными числами, во втором — удельным весом или частью каждой группы. Ряды распределения с абсолютными частотами характеризуют состав совокупности, а с относительными — их структуру. Ряды распределения с накопленными (кумулятивными) частотами указывают на количество или удельный вес единиц со значением признака, меньшим от заданного. Кумулятивные частоты находятся суммированием их по группам.
Атрибутивный ряд распределения – это ряд распределения, построенный по качественным признакам, не имеющим числового выражения и характеризующим свойство, качество изучаемого социально-экономического явления. Примером атрибутивных рядов могут служить распределения населения по полу, занятости национальности профессии и т. д.
Ряды распределения, построенные по количественному признаку, называются вариационными. Например, распределение населения по возрасту, рабочих – по стажу работы, заработной плате и т. д.
Вариационные ряды распределения состоят из двух элементов: вариантов и частот.
Вариантами называются числовые значения количественного признака в вариационном ряду распределения, они могут быть положительными отрицательными, абсолютными и относительными. Так, при группировке предприятий по результатам хозяйственной деятельности варианты положительные ( прибыль ) и отрицательные ( убыток ) числа.
Численности в каждой группе называют частотами ряда распределения. Сумма всех частот определяет численность всей совокупности или ее объем. Численности группы, выраженные в долях от общей численности единиц, называются частностями. Они выражаются в долях единиц или в процентах.
Вариационный ряд в зависимости от характера вариации подразделяются на дискретные и интервальные. Дискретный вариационный ряд распределения – это ряд, в котором группы составлены по признаку, изменяющемуся дискретно и принимающему только целые значения. Примером дискретного вариационного ряда распределения является распределение студентов по оценке, полученной на экзаменах.
Интервальный вариационный ряд распределения – это ряд, в котором группировочный признак может принимать в определенном интервале любые значения.
