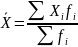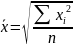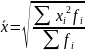16. Середні статистичні показники . Розрахунок та застосування середньої, арифметичної простої ,зваженої

Средние показатели.

Средняя величина – это обобщающая мера вариации и признаков характеризующая его уровень в расчете на единицу совокупности.

Различают две формы средних:

-простая- когда значения вариант наблюдаются в совокупности только 1 раз или одинаковое кол-ство раз

-взвешаная- когда значения вариант повторяются разное кол-ство раз.

Средняя арифметическая используются для усреднения прямых значений признаков путем их суммирования.

Простая	Взвешенная

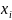- значение признака

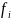- частоты показующие сколько раз встречаются каждое знач. Признака

n- объём совокупности

Пример:

200, 300, 100, 200, 300, 400, 300, 500, 400

17. Расчет и применение средней хронологической.

Средней хронологической называется величина, исчисленная из абсолютных величин, образующих ряды динамики.

Средняя хронологическая- используется для усреднения показателей, интервалы между которыми равные.

Ее расчет производится по формуле:

Средними хронологическими величинами пользуются для характеристики средних уровней явлений за определенные промежутки времени.

18. Расчет и применение средней гармонической.

Средняя гармоническая используется для усреднения обратных индивидуальных значений признаки путем их суммирования.

простая рассчитывается по формуле

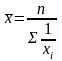взвешенная

19. Расчет и применение средней геометрической.

Средняя геометрическая – используется, когда объем явления является не суммой, а произведением значения признака.

Средняя геометрическая исчисляется извлечением корня степени из произведений отдельных значений — вариантов признака х:

где n — число вариантов.

Наиболее широкое применение средняя геометрическая получила в анализе динамики среднего темпа роста.

20. Розрахунок і застосування середньої квадратичної

Средняя квадратическая рассматривается как характеристика вариаций

Простая	Взвешенная

получила в анализе динамики среднего темпа роста.

21. Розрахунок структурних середніх

Для характеристики структуры вариационных рядов применяются так называемые структурные средние. Наиболее часто используются в экономической практике мода и медиана.

Мода – значение случайной величины встречающейся с наибольшей вероятностью. В дискретном вариационном ряду это вариант имеющий наибольшую частоту.

В интервальных вариационных рядах моду определяют приближенно по формуле

,

где - начальное значение интервала, содержащего моду;

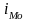- величина модального интервала;

- частота модального интервала;

- частота интервала, предшествующего модальному;

- частота интервала, следующего за модальным.

Мода применяется для решения некоторых практических задач. Так, например, при изучении товарооборота рынка берется модальная цена, для изучения спроса на обувь, одежду используют модальные размеры обуви и одежды и др.

Медиана - это численное значение признака у той единицы совокупности, которая находится в середине ранжированного ряда (построенного в порядке возрастания, либо убывания значения изучаемого признака). Медиану иногда называют серединной вариантов, т.к. она делит совокупность на две равные части.

В дискретных вариационных рядах с нечетным числом единиц совокупности - это конкретное численное значение в середине ряда. В интервальных вариационных рядах медиана определяется по формуле:

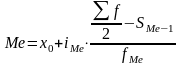, где

x₀ - нижняя граница медианного интервала;

i_Me - величина медианного интервала;

S_me-1 - сумма накопленных частот до медианного интервала;

f_Me - частота медианного интервала.