27) Характеристики вариации

Для измерения и оценки вариации используют абсолютные характеристики (вариационный размах, среднее линейное отклонение, среднеквадратическое отклонение) и относительные характеристики (коэффициенты вариации, неравномерности распределения).

а)абсолютные характеристики вариации:

Вариационный размах характеризует диапазон вариации, это разница между максимальным и минимальным значениями признака.

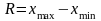
Середнее линейное отклонение – это середнее из модулей отклонений индивидуальных значений от центра распределения

;

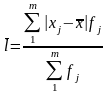Дисперсия – это средний квадрат отклонений индивидуальных значений признака от центра распределения

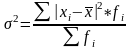
Середнее квадратическое отклонение – это корень квадратный из дисперсии

; .

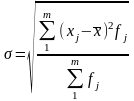По первичным, несгруппированным данным эти характеристики вариации рассчитываются по принципу простой средней, то есть:

; .

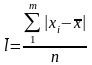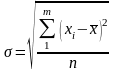Середнее квадратическое отклонение и среднее линейное отклонение по смыслу идентичны, но .

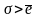Для альтернативного признака, вариация которого имеет два значения „да” и „нет”. дисперсия рассчитывается по формуле, как произведение долей:

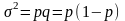
б)относительные характеристики вариации:

Сравнивая вариации разных признаков или одного признака в разных совокупностях используют относительные характеристики вариации. Коэфффициенты вариации рассчитываются как отношения абсолютных, именованных характеристик вариации (σ, 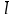, R) к центру распределения и часто выражаются процентами, то есть:

Линейный коэффициент вариации

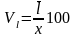
Квадратический коэффициент вариации

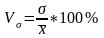
Коэффициент осцилляцииї

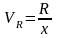
Чем менье среднее отклонение, тем более типична средняя, тем более однородна совокупность. Квадратический коэффициент вариации используют как критерий однородности совокупности. В симметричном, близком к нормальному, распределении V_s = 0,33.

Если: V < 10% - незначительная вариация, совокупность однородна;

10 % ≤ V ≤ 30% - середнее колебание, совокупность в пределах однородности, значение средней можна считать типичным уровнем признака в данной совокупности;

V > 33% - високий уровень вариации, совокупность неоднородна, значение средней нельзя считать типичным уровнем признака в данной совокупности.

28. Графічне зображення рядів розподілу

Для зображення варіаційного ряду використовують такі графіки: полігон, гістограму, кумуляту, огіву,тощо.

Полігон — це графічне зображення варіаційного ряду в прямокутній системі координат, коли ознака відкладається на осі абсцис, а частоти або частки (щільність розподілу) — на осі ординат.

Частіше за все полігон застосовують для зображення дискретного варіаційного ряду, однак його можна використовувати і для інтервального ряду.

Проілюструємо графічно ряди розподілу

За допомогою полігона можна визначити також моду, для цього з його вершини опускають перпендикуляр на вісь абсцис, а точка їхнього перетину і є модою. У наведеному прикладі мода відповідає врожайності 47 центнерів з гекгара озимої пшениці.

Гістрограма — це графічне зображення інтервального варіа­ційного ряду. На осі абсцис відкладають ознаки (варіанти). Утворені прямокутники пропорційні за висотою частотам значень ознаки для кожного інтервалу. В разі нерівних інтервалів висота прямокутників має бути пропорційною щільності розподілу ознаки у відповідному інтервалі.

Для графічного визначення моди за допомогою гістограми штриховими лініями сполучають верхні куги модального інтервалу і стовпчиків, що прилягають до нього. Модою є перетин осі абсцис перпендикуляром, опущеним з точки зіткнення цих прямих, як показано на рис. 1.5. Цей метод коректніше оцінює модальне значення, оскільки він враховує передмодальну і післямодальну частоти, тобто за гістограмою мода дорівнює 46,67 центнера з гектара. Графічне визначення моди можливе тільки у варіаційних рядках розподілу з рівними інтервалами.

Кумулятивні діаграми (кумуляти) використовують для графічного порівняння двох або більше варіаційних розподілів з рівними чи нерівними інтервалами. Для їх побудови використовують прямокутну систему координат, де на осі абсцис відкладають відрізки інтервалів групувань, а на осі ординат — нагромаджені частоти або частки. Висота прямокутників відповідає кумулятивним частотам або часткам певних інтервалів ряду розподілу. При побудові кумуляти інтервальної ознаки нижній межі першого інтервалу відповідає частота, яка дорівнює нулю, а верхній — частота першого інтервалу. Вершій межі другого і наступних інтервалів відповідають їхні нагромаджені частоти, а останнього інтервалу—сума всіх частот

Кумулятивна гісторама розподілу господарств регіону за врожайністю озимоїпшениці

На підставі кумулятивної кривої розподілу визначають скільки одиниць сукупності, або яка частка не перевищує певного значення групувальної ознаки. На рис. 8.8 штрихові лінії вказують на те що зі 100 господарств регіону 73 мали врожайність озимої пшениці менш ніж 47 центнерів з гектара.

Графічне визначення медіани: з точки на осі ординат яка відповідає півсумі нагромаджених частот SfМе, проводять штрихову лінію (рис. 1.8), паралельну осі абсцис. Перпендикуляр, опущений точки перетину цієі прямої з кумулятою на вісь абсцис укаже на медіану. В нашому прикладі Me = 45,5 центнера з гектара

При побудові кумуляти дискретної ознаки на осі абсцис відкладають значення варіантів, а на осі ординат - нагромаджені підсумки частот або часток. Сполучивши вершини ординат прямими лініями, дістанемо кумулятивну криву, яку ще називають кумулятивним полігоном.

Різновидом кумулятивного розподілу варіаційного ряду є огіва. Вона є дзеркальним відображенням кумуляти розподілу. При її побуві на осі абсцис відкладають нагромаджені частоти або частки, а на ординат — межі інтервалів варіаційного ряду розподілу.