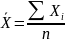15. Відносна величина структури
Статистичні сукупності завжди структуровані і мають певні складові. Відносна величина структури характеризує склад, структуру сукупності за тією чи іншою ознакою і показує внесок складових сукупності до загальної маси. Вона визначається відношенням розмірів складових частин сукупності до загального підсумку. Скільки складових, стільки відносних величин структури. Вони визначаються простим чи десятинним дробом або процентом. Наприклад, частка осіб допрацездатного віку міста становить 1/4, або 0,25, або 25%.
16. Середні статистичні показники . Розрахунок та застосування середньої, арифметичної простої ,зваженої
Средние показатели.
Средняя величина – это обобщающая мера вариации и признаков характеризующая его уровень в расчете на единицу совокупности.
Различают две формы средних:
-простая- когда значения вариант наблюдаются в совокупности только 1 раз или одинаковое кол-ство раз
-взвешаная- когда значения вариант повторяются разное кол-ство раз.
Средняя арифметическая используются для усреднения прямых значений признаков путем их суммирования.
Простая |
Взвешенная |
|
|
-
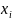значение признака
-
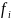частоты показующие сколько раз встречаются
каждое знач. Признака
n- объём совокупности
Пример:
200, 300, 100, 200, 300, 400, 300, 500, 400
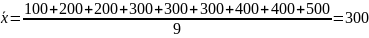
17. Средняя хронологическая
Средней хронологической называется величина, исчисленная из абсолютных величин, образующих ряды динамики.
Средняя хронологическая- используется для усреднения показателей, интервалы между которыми равные.
Ее расчет производится по формуле:
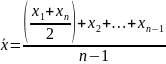
Средними хронологическими величинами пользуются для характеристики средних уровней явлений за определенные промежутки времени.
18. Средняя гармоническая
Наряду со средней арифметической, в статистике применяется средняя гармоническая величина, обратная средней арифметической по обратным значениям признака. Как и средняя арифметическая, она может быть простой и взвешенной. Применяется она тогда, когда необходимые веса (fi) в исходных данных не заданы непосредственно, а входят сомножителем в одни из имеющихся показателей.
Средняя гармоническая простая рассчитывается по формуле
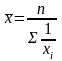
т.е. это обратная величина средней арифметической простой из обратных значений признака.
19. Розрахунок на застосування середньої геометричної
Средняя геометрическая применяется в тех случаях, когда индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики, т.е. характеризует средний коэффициент роста.
Средняя геометрическая – используется, когда объем явления является не суммой, а произведением значения признака.
Средняя геометрическая исчисляется извлечением корня степени из произведений отдельных значений — вариантов признака х:
где n — число вариантов.
Наиболее широкое применение средняя геометрическая получила в анализе динамики среднего темпа роста.