Содержание

Введение 3

1 Описание и аналитические исследования процесса 4

2 Описание и анализ аппаратов проектируемого процесса 11

Барабанный вакуум-фильтр (рисунок - 2.8). Фильтр имеет вращающийся цилиндрический перфорированный барабан 1, покрытый металлической сеткой 2 и фильтровальной тканью 3. Часть поверхности барабана (30–40%) погружена в суспензию, находящуюся в корыте 6. С помощью радиальных перегородок барабан разделен на ряд изолированных друг от друга ячеек (камер) 9. 18

3 Инженерные расчёты 21

Заключение 26

Список использованной литературы и информационных источников: 27

Введение

Целью данного курсового проекта является более углубленное изучение гидромеханических процессов, а именно процесса фильтрования.

Важной задачей курсового проекта является определение места и экономической роли процесса фильтрования в технологическом прогрессе соответствующих производств, в виде сравнения действующих аппаратов и наиболее совершенных по показателям технологическим, экономическим, энергетическим и т.п.

Процессы в пищевой технологии в большинстве своем сложны и зачастую представляют собой сочетание гидродинамических, тепловых, массообменных, биохимических и механических процессов. Одним из важных процессов является фильтрование. Фильтрование может быть шламовым, оно реализуется для маловязких жидкостей, содержащих большое количество взвешенных частиц; закупорочным – при малом размере частиц и их небольшом количестве; и комбинированным.

Тема моего курсового проекта достаточно актуальна в наше время, поскольку процессы фильтрования очень широко используются в пищевой промышленности. Значение процессов фильтрования возрастает с увеличением масштабов производства. Знания физических основ процесса, факторов, задающих режимы работы и качества производимого продукта, позволяет учёным наиболее полно использовать рациональные типы современного оборудования фильтрации.

1 Описание и аналитические исследования процесса

К гидромеханическим процессам относятся осаждение взвешенных в жидкой или газообразной среде частиц под действием гравитационной силы (осаждение), центробежной силы (центробежное осаждение) или сил электрического поля; фильтрование жидкостей или газов через пористую перегородку под действием разности давлений (фильтрование и центробежное фильтрование); перемешивание в жидкой среде; псевдоожижение и другие [1].

Фильтрование – это разделение неоднородной системы с твердой дисперсной фазой, основанное на задержании твердых частиц пористыми перегородками.

Фильтрование осуществляется под действием разности давлений перед фильтрующей перегородки и после нее. Интенсивность фильтрования зависит от количества суспензий, полученных на предыдущих стадиях технологического процесса: дисперсной системы с понижением сопротивления осадка, без смолистых, слизистых и коллоидных веществ.

При разделении неоднородных систем фильтрования возникает необходимость выбора конструкции фильтра, фильтровальной перегородки, режима фильтрования.

В качестве фильтрующих материалов применяют зернистые материалы – песок, гравий для фильтрования воды, различные ткани, картон, сетки, пористые полимерные материалы, керамику и т.д.

Классификация процесса фильтрования

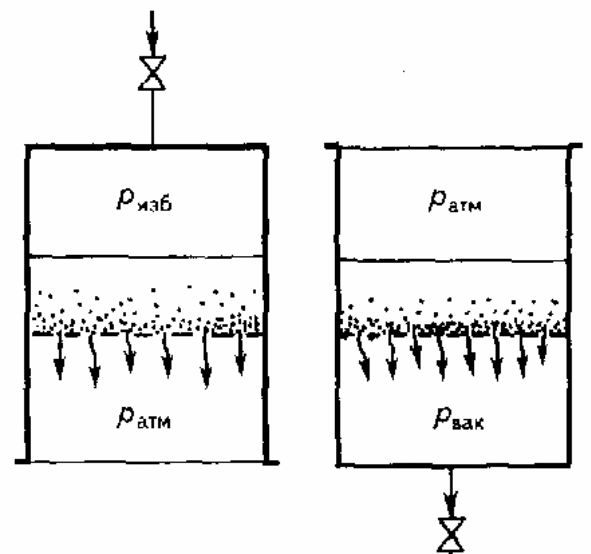
1) По движущей силе: движущей силой процесса фильтрования является разность давлений по обе стороны фильтровальной бумаги. Получить разность можно двумя способами:

– создание избыточного давления над фильтром (рисунок 1, а)

– создание вакуума (рисунок 1, б) [3].

2. По механизму фильтрования:

– с образованием осадка на поверхности фильтровальной перегородки. При этом твердые частицы не проникают внутрь перегородки.(рисунок 2, а)

– с закупориванием пор фильтровальной перегородки, твердые частицы проникают внутрь перегородки (рисунок 2,б).

- промежуточный вид фильтрования имеет место в случае одновременного закупоривания пор фильтровальной перегородки и отложения осадка на поверхности фильтровальной перегородки [2].

3) По целенаправленности процесса:

– получение чистого осадка;

– получение фильтрата;

– получение одновременно осадка и фильтрата;

4) По целевому назначению:

– очистное фильтрование, его применяют для очистки растворов от включений, а целевым продуктом является фильтрат.

– продуктовое фильтрование, его целью является получение осадка (НУТЧ-фильтры, барабанные вакуум фильтры).

а б

Рисунок 1 – Схема фильтрования: а – под избыточным давлением;

б – под вакуумом

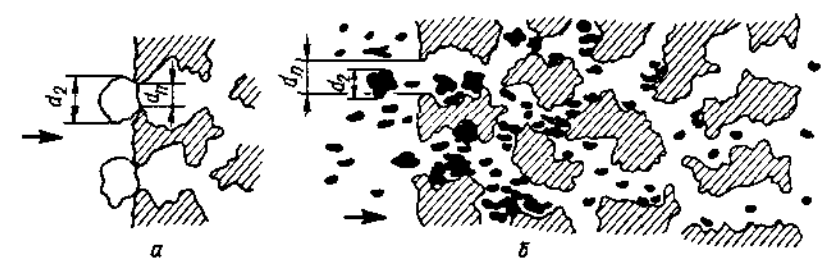
Рисунок – 2 Схемы фильтрования:

а - с образованием осадка; б – с закупориванием пор

Процесс разделения суспензий на фильтрах состоит из нескольких операций: промывка осадка на фильтре, при этом с помощью фильтра, фильтрат выделяется из пор осадка; продувка осадка воздухом с целью вытеснения из пор оставшейся промывной жидкости; сушка осадка нагретым воздухом [3].

Фильтрование обычно протекает в ламинарном режиме. Скорость фильтрования – это объем фильтрата полученный с 1м² фильтрующей поверхности за 1с:

ω= , [м³/м²×с]. (1)

Скорость процесса прямо пропорциональна разности давлений и обратно пропорциональна сопротивлению осадка. Процесс описывается следующим кинетическим уравнением:

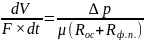, (2)

где V – объем фильтрата, м³;

F – площадь поверхности фильтрования, м²;

t-продолжительность фильтрования, с;

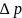– перепад давлений, Н/м²;

– вязкость жидкой фазы, Н×с/м²;

R_ос – сопротивление осадка, м^-1;

- сопротивление фильтровальной перегородки, м^-1.

Общее уравнение фильтрования (2) необходимо интегрировать по-разному в зависимости от следующих условий проведения процесса:

· фильтрование при постоянной движущей силе;

· фильтрование при постоянной скорости;

· фильтрование при постоянных движущей силе и скорости;

· фильтрование при переменных движущей силе и скорости.

Поскольку в практике большинство фильтров работает в режиме постоянной движущей силы, а промывку можно рассматривать как фильтрование при постоянных движущей силе и скорости:

Д ля случая фильтрования при Δр = const из уравнения (2) после его интегрирования в пределах 0 V и 0 τ получим

(3)

Полученное уравнение применимо как к сжимаемым, так и к несжимаемым осадкам и показывает, что с увеличением объема фильтрата скорость фильтрования уменьшается.

Для случая фильтрования при v = const из уравнения (2) получим

(4)

Если предположить, что в фильтровальную перегородку не проникают твердые частицы, то сопротивление можно принять постоянным, а сопротивление осадка изменяется с увеличением слоя осадка.

Примем, что при прохождении 1 м³ фильтрата, образуется х₀ м³ осадка, тогда:

х₀V=h₀F, h₀= х₀V/F, (5)

где h₀-высота осадка, м.

Допустим, что сопротивление слоя осадка пропорционально его высоте:

R_oc r₀h₀=r₀x₀V/F, (6)

где r₀ – удельное сопротивление осадка, м^2.

Подставив, полученное выражение в уравнение (2):

(7)

Пренебрегая, сопротивлением фильтровальной перегородки получим:

(8)

Для начального момента фильтрования (V=0):

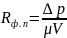(9)

Для случая фильтрования при имеем:

(10)

Полученное уравнение применимо как к сжимаемым, так и к несжимаемым осадкам и показывает, что увеличением объема фильтрата скорость фильтрования уменьшается.

Из этого уравнения можно найти продолжительность фильтрования:

( )² + (11)

Таким образом, продолжительность фильтрования прямо пропорциональна квадрату объема полученного фильтрата. [3]

Материальный баланс для процесса фильтрования составляют для определения производительности фильтровальной установки по осадку, фильтрату или исходной суспензии. Соответствующие уравнения имеют вид:

• для всей гетерогенной системы

G_с = G_ф + G_ос , (12)

где G_с - производительность фильтра по суспензии

G_ф – производительность фильтра по фильтрату

G_ос - производительность фильтра по осадку

• для твердой фазы

G_с · Х_ос = G_ос · Х_ос , (13)

где Х_с, Х_ос - соответственно массовая концентрация суспензии и осадка

или

G_с · Х_с = G_ос(1 - W), (14)

где W = (1 - Х_ос) – влажность осадка.

Массовая концентрация в осадке равна

X_ос = W – 1 (15)

Переход от весовых величин к объемным осуществляем с помощью плотностей соответствующих потоков (фаз). При этом плотность суспензии определяется в зависимости от способа выражения концентрации твердой фазы по уравнениям:

• Плотность осадка:

ρ_ос = 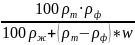, (16)

• Плотность суспензии:

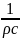= , (17)

ρ_с = , (18)

Удельная производительность фильтрата в (м³/м²):

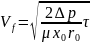
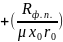² - (19)

Фильтрование под действием центробежной силы проводят в фильтрующих центрифугах. Фильтрующая центрифуга в отличие от отстойной имеет перфорированный барабан, об­тянутый внутри фильтровальной тканью. Суспензия под действи­ем центробежной силы отбрасывается на фильтровальную ткань. Дисперсионная жидкая фаза фильтруется через ткань, фильтрат выводится из центрифуги, а взвешенные частицы задерживаются на фильтровальной ткани, образуя осадок.

Процесс фильтрования можно разделить на три периода: обра­зование осадка, его уплотнение и отжим.

При центробежном фильтровании на массу элементарного кольца суспензии действует центробежная сила

(20)

где - масса элементарного кольца, кг;

- угловая скорость ( = ), с ^-1;

r – расстояние кольца от оси вращения, м.

Отношение центробежной силы к силе тяжести, как было Указано выше, является фактором разделения, характеризую­щим эффективность разделения суспензии в центрифуге. Фак­тор разделения возрастает пропорционально квадрату угловой скорости вращения барабана центрифуги и уменьшению его ди­аметра.

Производительность фильтрующих центрифуг рассчитывают исходя из теории фильтрования. Движущая сила процесса, дей­ствующая на элементарный объем суспензии dV = 2πrLdr (рисунок 3) :

( 21)

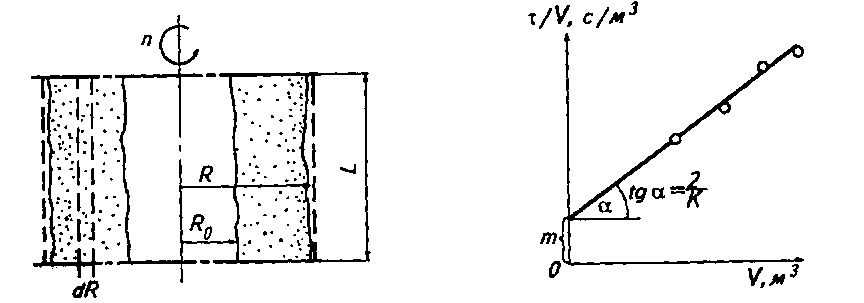
Рисунок 4 -К расчёту производительности Рисунок 5 - К определению констант

фильтрующих центрифуг фильтрования

Движущую силу найдем, проинтегрировав полученное выраже­ние в пределах от R₀ до R: Δр_и = р_сω² (R² –R₀² )/2.

Скорость центробежного фильтрования

=0,5 , (22)

где R_ф.п. – сопротивление фильтрующей перегородки;

r₀ – удельное сопротивление слоя осадка;

х₀ – толщина слоя осадка, которая для непрерывно действующих центрифуг не изменяется во времени;

R, R₀ – соответственно внешний и внутренний радиусы барабана центрифуги.

На практике отношение объема осадка х₀ к объему фильтрата V, удельное объемное сопротивление осадка r₀ и сопротивление фильтровальной перегородки R_ф.п определяют экспериментальным путём.

У равнение (4) при F 1 м² может быть представлено в виде

, (23)

где С - константа фильтрования, характеризующая гидравлическое сопротивление фильтрующей перегородки м³\м²;

К – константа фильтрования, учитывающая режим фильтрования и физико - химические свойства осадка и жидкости, м²\с

Уравнение (23) представляет собой уравнение прямой линии, наклоненной к горизонтальной оси под углом α, тангенс которого tgα = 2/K, и отсекающей на оси ординат отрезок т = 2С/К (рисунок 5). Для построения этой линии откладывают по оси абсцисс измеренные значения V_1,V₂,...,V_п а по оси ординат — соответствующие значения τ₁/V₁, τ₂ V₂,…,τ_п/ V_n.