Контрольная работа по дисциплине

Методы оптимальных решений

Вариант 8.

Параметры m и n определяются по двум последним цифрам номера студента в группе в соответствии со следующим правилом:

Пусть yz – двузначный номер студента. Тогда:

y	0	1	2	3	4
m	4	3	5	1	2

z	0	1	2	3	4	5	6	7	8	9
n	3	2	1	4	5	3	1	5	2	4

По условию: (1)

1. Линейное программирование

Предприятие планирует выпуск двух видов продукции Р₁ и Р₂, на производство которых расходуется три вида сырья S₁, S₂ и S₃.

В таблице указаны затраты каждого вида сырья на производство 1 единицы каждого вида продукции, запасы сырья и прибыль от реализации 1 единицы каждого вида продукции:

Виды сырья	Затраты сырья (ед.) на производство 1 единицы продукции		Запасы сырья
	Р1	Р2
S1	n	2	m·n+5n
S2	1	1	m+n+3
S3	2	m+1	m·n+4m+n+4
Прибыль от реализации 1 ед. прод.	m+2	n+1
План пр-ва (ед. прод.)	x1	x2

Дополнительное ограничение: в сумме требуется изготовить не менее, чем n единиц продукции.

Задание:

1. Записать математическую модель задачи (систему ограничений и целевую функцию), предполагая, что оптимальным считается план производства, обеспечивающий максимально возможную прибыль от реализации продукции.

2. На плоскости Оx₁x₂ построить область допустимых решений и найти оптимальное решение (оптимальный план производства) геометрическим методом.

Решение

С учетом (1):

Виды сырья	Затраты сырья (ед.) на производство 1 единицы продукции		Запасы сырья
	Р1	Р2
S1	2	2	10
S2	1	1	9
S3	2	5	30
Прибыль от реализации 1 ед. прод.	6	3
План пр-ва (ед. прод.)	x1	x2

1. Математическая модель задачи: (и), предполагая, что оптимальным считается план производства, обеспечивающий максимально возможную прибыль от реализации продукции.

– система ограничений:

(2)

– целевая функция: (3)

Т.о., необходимо при заданных ограничениях (2) найти значения переменных х₁ и х₂, при

которых целевая функция F принимает максимальное значение.

2. На плоскости Оx1x2 построить область допустимых решений и найти оптимальное решение (оптимальный план производства) геометрическим методом.

Решение.

Преобразуем исходную систему:

.

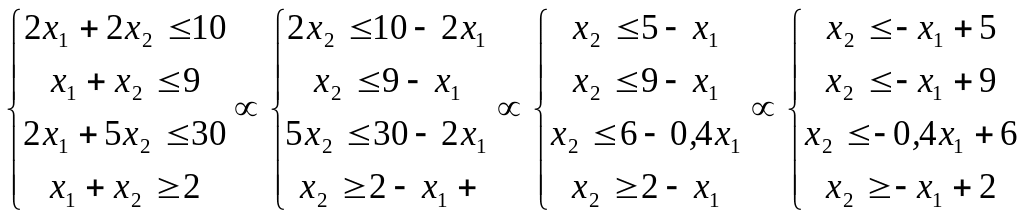
Строим область допустимых планов ЗЛП, графически решая систему неравенств с учетом двух последних неравенств при помощи табличного процессора MS Excel (см. рис. 1)

Таблица 1.1

Рисунок 1.

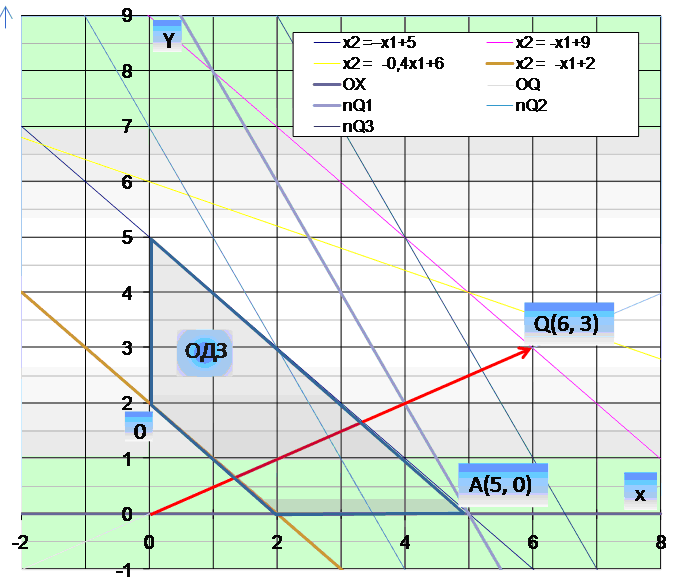
Координаты угловых точек области допустимых значений ОДЗ (5;0); (2;0), (0,2) и (0;5) определяются по графику как координаты точек пересечения граничных линий области допустимых планов.

Cтроим вектор градиента целевой функции F: gradQ , координаты которого равны соответствующим коэффициентам при x₁ и x₂ в выражении целевой функции F. После этого проводим семейство nQ1, nQ2, nQ3 линий уровня целевой функции F перпендикулярных вектору градиента Q: .

Целевая функция достигает своего максимума, если двигать линию уровня параллельно самой себе в направлении grad Q. При этом линия уровня выходит из области допустимых планов угловой точке А(5;0). Следовательно, план x_1,2^* =(5;0) является оптимальным в решаемой ЗЛП на максимум.

x_1max^*= 5; x_2max^*=0; F_max = .

Ответ: x_max^*= (5; ); F_max = 30.