Практическая работа № 11

Тема 2.5. Финансы предприятий

Цели:

• Закрепление теоретических знаний по теме «Финансы предприятий»;

• Формирование практических навыков в дисконтировании капитала и дохода

Теоретическая часть:

Деньги, являясь специфическим товаром, со временем меняют свою стоимость и, как правило, обесцениваются. Изменение со временем стоимости денег под влиянием ряда факторов, важнейшими из которых являются инфляция и способность денег приносить доход при условии их разумного инвестирования в альтернативные проекты (упущенная выгода).

Приведение денежных сумм, возникающих в разное время, к сопоставимом виду называется временной оценкой денежных потоков.

Для правильной оценки будущих поступлений производят временную корректировку с помощью дисконтирования и сложного процента.

Дисконтирование – метод оценки стоимости суммы, которая будет получена в будущем; определение стоимости на некоторый момент времени при условии, что в будущем она составит заданную величину.

Простые проценты – ставка, которая применяется к одной и той же начальной сумме на протяжении всего срока суды.

Сложные проценты с однократным начислением – процент, выплачиваемый и на проценты, начисленные ранее, и на основную сумму один раз в году. Сложные проценты с многократным начислением – процент, выплачиваемый и на проценты, начисленные ранее, и на основную сумму несколько раз в году.

Будущая стоимость денег (наращенная сумма) (FV) – первоначальная сумма (PV) с начисленными процентами к концу срока. Тип решаемых задач: определение будущей стоимости текущей денежной суммы.

Вид начисления	Наращение
Ссудные проценты
Простые проценты	FV = PV (1+ni)
Сложные проценты с однократным начислением	FV = PV (1+ic)n
Сложные проценты с многократным начислением	FV = PV (1+j/m)nm
Учетные проценты
Простые проценты	FV = PV / (1-nd)
Сложные проценты с однократным начислением	FV = PV / (1-dc)n
Сложные проценты с многократным начислением	FV = PV / (1-dc/m)nm

Условные обозначения:

FV – будущая стоимость (наращенная сумма);

PV – настоящая (современная, приведенная, текущая) стоимость;

i – годовая ставка простого ссудного процента;

i_c – годовая ставка сложного ссудного процента с однократным начислением;

j – годовая ставка сложного ссудного процента с многократным начислением;

d – годовая ставка простого учетного процента;

d_c – годовая ставка сложного учетного процента;

n – общее число лет;

m – число начислений процентов (капитализаций) в году.

Приведенная (современная, настоящая, текущая) стоимость денег (PV) – постоянная база для расчета. Первоначальная сумма, дисконтированная на начало срока ренты.

Тип решаемых задач: определение текущей стоимости денежной суммы, которая будет получена в будущем.

Вид начисления		Дисконтирование
Ссудные проценты
Простые проценты		PV = FV / (1+ni)
Сложные проценты с однократным начислением		PV = FV / (1+ic)n
Сложные проценты с многократным начислением		PV = FV / (1+j/m)nm
Учетные проценты
Простые проценты	PV = FV (1-nd)
Сложные проценты с однократным начислением	PV = FV (1-dc)n
Сложные проценты с многократным начислением	PV = FV (1-dc/m)nm

Порядок выполнения работы:

Задание:

1. Провести дисконтирование капитала и дохода;

2. Сделать соответствующие выводы, с их обоснованием;

3. Работу аккуратно оформить.

Примечание:

1. Вариант задания определяет преподаватель;

2. Работа может выполняться как индивидуально, так и ма­лыми группами (до трёх человек);

3. Необходимые рекомендации и пояснения по выполнению работы даёт преподаватель.

Задач 1.

Имеются следующие данные о динамике процентных ставок и величине совокупного дохода от инвестиций:

Группа доходов	Базисный год				Отчетный год
	ставка налога, % i0	налого-облагаемая база V0	взыскано налогов, д.е. i0V0	ставка налога, % i1		налого-облагаемая база V1	взыскано налогов, д.е. i1V1
1	12	245	29,4	13		510	66,3
2	20	265	53	13		292	37,96
3	20	302	60,4	13		347	45,11
Итого	-	812	142,8	-		1149	149,37

Определите:

1. Среднюю процентную ставку налога за каждый год в целом по группам доходов.

2. Прирост перечисленного в бюджет налога в целом по группам доходов в отчетном периоде по сравнению с базисным.

3. Относительное и абсолютное изменение поступлений по налогам в отчетном периоде по сравнению с базисным в целом и в том числе за счет изменения ставки налога и изменения налогооблагаемой базы.

Решение

1. Найдем среднюю ставку по налогам:

– по предполагаемому исполнению суммы налога:

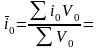
– по фактическому исполнению:

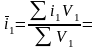
2.ΔН=Н₁-Н₀ =

3.

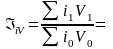
ΔiV = i₁ V₁- i₀ V₀ = 149,37-142,8=6,57 руб.

Влияние факторов:

– изменения ставок налога:

,

=

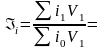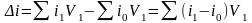– изменения налогооблагаемой базы:

=.

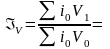
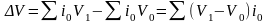Проверка:

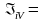
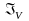= ΔiV=Δi+ΔV.

Задача 2. Под какую годовую процентную ставку выгоднее взять кредит: 11% сложную с начислением один раз в году или 10% сложную с начислением процентов 12 раз в год? Показать таблично и графически наращенные суммы для кредита величиной 20000 руб. при этих двух процентных ставках за 0...4 года с шагом 0,5 года.

Решение

Сравним коэффициенты наращения.

Коэффициент наращения по сложным процентам с начислением один раз в году: Кн (i_c) =(1+i_c)ⁿ =

Коэффициент наращения по сложным процентам с многократным начислением: Кн (j) =(1+j/m)^nm =

Наращенная сумма по сложным процентам с однократным начислением рассчитывается по формуле: FV = PV (1+i_c)ⁿ .

Наращенная сумма по сложным процентам с многократным начислением рассчитывается по формуле: FV = PV (1+j/m)^nm .

Наращенные суммы для кредита 20000 руб.

Срок n, лет	FV (iс = 11%)	FV (j = 10%, m = 12)	FV = FV (ic) – FV (j)
0,0	20000(1+0,11)0=	20000(1+0,1/12)12*0=
0,5	20000(1+0,11)0,5=	20000(1+0,1/12)12*0,5=
1,0	20000(1+0,11)1=	20000(1+0,1/12)12*1=
1,5	20000(1+0,11)1,5=	20000(1+0,1/12)12*1,5=
2,0	20000(1+0,11)2=	20000(1+0,1/12)12*2=
2,5	20000(1+0,11)2,5=	20000(1+0,1/12)12*2,5=
3,0	20000(1+0,11)3=	20000(1+0,1/12)12*3=
3,5	20000(1+0,11)3,5=	20000(1+0,1/12)12*3,5=
4,0	20000(1+0,11)4=	20000(1+0,1/12)12*4=

Задача 4. Под какую годовую процентную ставку выгоднее сделать вклад сроком на 5 лет: 21% простую или 20% сложную с начислением процентов 4 раза в год? Показать таблично и графически наращенные суммы для вклада величиной 20000 руб. при этих двух процентных ставках за 0...4 года с шагом 0,5 года. Отметить на графике срок, при котором ставки эквивалентны. Указать области, в которых каждая ставка выгоднее другой.

Решение Сравним коэффициенты наращения

Коэффициент наращения по простым процентам:

Кн (i) = (1+ni) =

Коэффициент наращения по сложным процентам с многократным начислением: Кн (j) = (1+j/m)^nm

Наращенная сумма по простым процентам рассчитывается по формуле:

FV = PV (1+ni).

Наращенная сумма по сложным процентам с многократным начислением рассчитывается по формуле: FV = PV (1+j/m)^nm .

Срок n, лет	FVпрост (i = 21%)	FVсложн (j = 20%, m = 4 )	FV = FVпрост – FVсложн
0,0	20000(1+0*0,21)=	20000(1+0,2/4)4*0=
0,5	20000(1+0,5*0,21)=	20000(1+0,2/4)4*0,5=
1,0	20000(1+1*0,21)=	20000(1+0,2/4)4*1=
1,5	20000(1+1,5*0,21)=	20000(1+0,2/4)4*1,5=
2,0	20000(1+2*0,21)=	20000(1+0,2/4)4*2=
2,5	20000(1+2,5*0,21)=	20000(1+0,2/4)4*2,5=
3,0	20000(1+3*0,21)=	20000(1+0,2/4)4*3=
3,5	20000(1+3,5*0,21)=	20000(1+0,2/4)4*3,5=
4,0	20000(1+4*0,21)=	20000(1+0,2/4)4*4=