Варианты заданий 3.6 и 3.7

Вариант	f(х)	Вариант	f(х)	Вариант	f(х)

Задание 3.8.

1. Транспонируйте матрицу М с помощью операции Symbolics  Matrix  Transpose.

2. Инвертируйте матрицу с помощью операции Symbolics  Matrix  Invert.

3. Вычислите определитель матрицы с помощью операции Symbolics  Matrix  Determinant.

Задание 3.9. Вычислите пределы.

1. 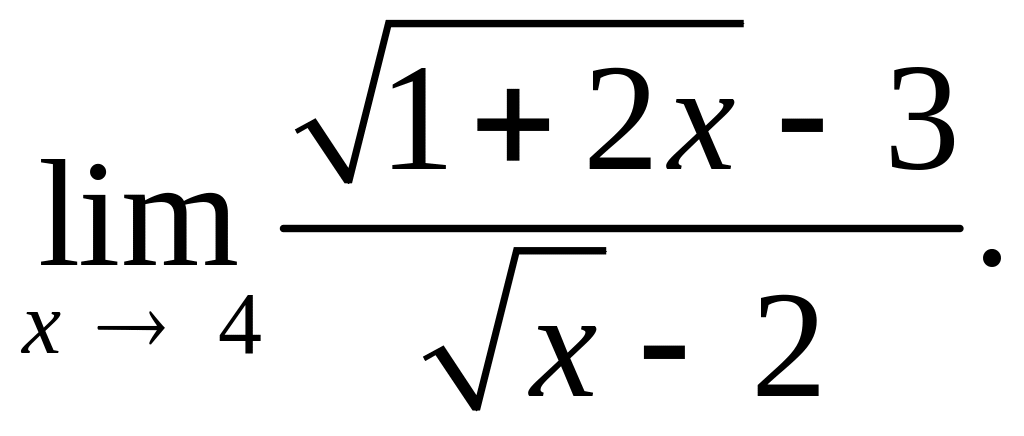2.

3. 4.

Задание 3.10. Найдите сумму ряда.

1. . 2.

Задание 3.11. Найдите производную и упростите выражение.

1.

2.

Задание 3.12. Вычислите неопределенные интегралы.

1. 2.

Задание 3.3. Вычислите определенные интегралы.

1. 2.

Лабораторная работа 4. Решение алгебраических и трансцендентных уравнений

Компьютерные технологии решения алгебраических и трансцендентных уравнений представляют собой выполнение следующих процедур:

1. определение области изоляции каждого из вещественных корней уравнения;

2. выбор встроенной в MathCAD функции решения уравнения;

3. решение уравнения; проверка достоверности полученного решения.

Система MathCAD для определения корней алгебраических и трансцендентных имеет три функции: root, Find, polyroots.

4.1.Решение уравнений с помощью функции root

Функция root осуществляет решение алгебраических и трансцендентных уравнений, определяя вещественные корни уравнений. MathCAD в функции root использует для поиска корня метод секущих.

Она имеет вид:

root(f(x),x), где:

• f(x) – решаемое уравнений f(x);

• x – аргумент функции f(x) (искомое неизвестное уравнения).

При использовании функции root задаётся начальное приближение корня x0.

Функция root представляется в одной из следующих форм:

1-ый вариант 2-ой вариант 3-ий вариант

x:=x0	x:=x0	x:=x0
Root (f(x),x)=	z=root (f(x),x)	(x):=f(x)
	z=	z:=root((x),x)
		z=

Если после многих итераций MathCAD не может найти решение, то появляется сообщение: «отсутствует сходимость». Эта ошибка может быть вызвана следующими причинами:

• уравнение не имеет корней;

• корни уравнения расположены далеко от начального приближения;

• функция f(x) имеет локальные экстремумы между начальным приближением и корнем;

• функция f(x) имеет разрывы между начальным приближением и корнем;

• функция f(x) имеет комплексный корень, но начальное приближение было вещественным.

Чтобы установить причину ошибки рекомендуется построить график функции f(x). Он поможет выяснить наличие корней уравнения, определить начальные приближения.

Пример 4.1. Решить уравнение: 3 ^X - 1.6*e^X+ 4=0.

Технология выполнения задания.

Определим количество корней уравнения и их интервалы изоляции. Для этого:

1. задаём ранжированную переменную x=0.1,0.5..5 (примерный диапазон изменения) и заданное уравнение без правой его части (=0).

2. Набираем x= (на экране появляется диапазон изменения x;)

3. Набираем f(x)= (на экране появляется диапазон изменения заданного уравнения).

4. В системе MathCAD выполнить команды ViewToolbars  Graph. На появившейся панели Graph щёлкнуть по кнопке XY – Plot.

5. Построить график заданного уравнения (см. рис. ).

6. Определить по графику интервалы изоляции корней.

Построение графика заданного уравнения представлено на рис.4.1.

Рис. 4.1. График уравнения 3^Х – 1,6e^X+4

По графику интервалы изоляции корней x₁ и x₂ соответственно равны: 2.5<x₁<2.9 и 4<x₂<4.5.

Решение уравнения приведено на рис.4.2.

x:=2.5

root(3^Х – 1.6exp(x)+4,x)=2.541

x:=4.5

root(3^Х – 1.6exp(x)+4,x)=4.473

Рис. 4.2. Решение уравнения 3^Х – 1,6*e^X+4

Проверить правильность определения корней, подставив полученные решения в исходное уравнение.

Решение уравнений с помощью функции

Функция Find предназначена для решения систем уравнений методом итераций. Как частный случай, функция может определять корни одного уравнения.

Решение уравнения выполняется в следующей последовательности:

1. задать начальное приближение корня х₀ из области его изоляции;

2. написать слово Given, указывающее на то, что далее следует заданное уравнение;

3. написать заданное уравнение. Следует иметь в виду, что при вводе в уравнение знака равенства необходимо нажать клавиши <Ctrl>+<=>;

4. написать функцию Find(x), где x – искомое неизвестное;

5. нажать клавишу <=>.(знак равенства).

Технология решения уравнения 3^Х - 1,6е^Х+4 приведена на рис. 4.3.

X:=2.5 Given 3Х – 1.6exp(x)+4,x=0 Find(x)=2.541

X:=4.5 Given 3Х – 1.6exp(x)+4,x=0 Find(x)=4.472

Рис. 4.3. Решение уравнения 3^Х – 1,6e^X+4

Определение корней многочлена с помощью функции polyroots

Корни многочлена обычно определяются с помощью функции polyroots, которая имеет вид:

polyroots (V),

где V – вектор коэффициентов многочлена, начиная с младшей степени.

Функция находит все вещественные и комплексные корни.

Технология решения задачи состоит в следующем:

• ввести символ присвоения имени вектора-столбца, например V:=;

• нажать комбинацию клавиш Ctrl+M. На экране появляется окно Insert Matrix. В полях Rows и Columns устанавливается число строк и число столбцов матрицы. Для случая определения корней полинома число столбцов равно 1, а число строк – (n+1), где n степень многочлена. После щелчка по кнопке ОК в окне, на экране появляется пустой шаблон вектора- столбца размером (n+1) ×1;

• заполнить маркеры ввода вектора коэффициентами заданного полинома, в первой строке пишется коэффициент свободного члена (коэффициент при нулевой степени полинома);

• написать polyroots (V);

• нажать клавишу  (равно) на клавиатуре. На экране появится ответ в виде вектора корней.

Пример 4.2. Решить уравнение x⁴+3x³-7x+3.5=0

Технология выполнения задания приведена на рис. 4.4.

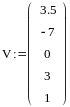
Рис. 4.4. Решение уравнения x⁴+3x³-7x+3.5=0.

Возьмите из Задания 4.1 и Задания 4.2 свой вариант уравнения и найдите его корни используя функцию root и функцию polyroots. Убедитесь, что найденные значения действительно являются корнями Вашего уравнения.

Задание 4.1. Найти все корни заданного уравнения, используя функцию root

№п.п.	Уравнение f(x)	№ п.п.	Уравнение f(x)
	4sin x + x2 - 2=0		(x - 1)2 - 0.5exp( - x) – 2=0
	3X-4.5x-5.6=0		2/x+x2 + ex – 8=0
	3 sinx +0.35x-8x=0		tgx + x + 2=0
	0.25x2+x-1.25002=0		ctgx – 2x + 2=0
	0.1x2-xlnx=0		-x2 + cos (x+1) + 3=0
	3x - 4lnx-5=0		2ln(2–x)–x + ex – 10=0
	ex - e –x -2=0		1/x + ln(2x + 4) – 3=0
	ex + lnx – 10x=0		x cos x + 1.5=0
	sin x2+cos x2-10x=0		2x5 – lnx – 7x2=0
	x2-ln(1+x)-3=0		xsinx x + 1.5=0
	2xsin x – cosx=0		x2x – 4x2 + 1.5=0
	lnx – x + 1.8=0		2.5x – 8.6x – 3.5=0
	0.6 3x – 2.3x – 3=0		ln(x + 2) + 2x2 - 9x + 2=0
	2x – 4x=0		xln(2.5x) – 1.5x + 1.5=0
	3x – ex + 4=0		xtgx – 1/3=0

Задание 4.2. Найти все корни заданного уравнения, используя функцию polyroots

Для полинома g(x) выполнить следующие действия:

1. с помощью команды Symbolics  Polynomial Coefficients (Коэффициенты полинома) создать вектор V, содержащий коэффициенты полинома;

2. решить уравнение g(x) = 0 с помощью функции polyroots;

3. решить уравнение символьно, используя команду Symbolics  Variable Solve

№ варианта	Уравнение
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16	x5 – 2.2x3 + 0.5x2 – 7x – 3.4
17	x5-3.2x3+2.5x2-7x-2.4
18	x5-5.2x3+2.5x2-7x-2.4
19	x5-4.2x3+3.5x2-7x-7.4
20	x5-2.2x3+7.5x2-7x-3.9
21	x5-2.9x3+6.5x2-7x-5.4
22	x5-3.2x3+9.5x2-7x-7.5
23	x5-3.5x3+2.5x2-7x+6.4
24	x5-9.2x3+5.5x2-7x+1.4
25	x5-8.2x3+4.5x2-7x+6.5
26	x5-3.2x3+2.5x2-7x+1.5
27	x5-7.2x3+9.5x2-7x+2.5
28	x5-5.2x3+5.5x2-7x+3.5
29	x5-1.2x3+8.5x2-7x+4.5
30	x5-3.2x3+1.5x2-7x+9.5

Лабораторная работа 5. Решение систем уравнений

Системы уравнений могут быть линейные и нелинейные, с постоянными и переменными коэффициентами. Решение таких уравнений возможно аналитическими и численными методами.

В среде MathCAD системы уравнений решаются с помощью функций lsolve, Find, Minerr. Максимальное число уравнений и переменных равно 50. Результатом решения системы будет численное значение искомого корня.

Функция lsolve позволяет решать системы линейных алгебраических уравнений матричным методом

Функция Find решает системы линейных и нелинейных уравнений методом итераций.

Функция Minerr, также как и функция Find, решает системы линейных и нелинейных алгебраических уравнений. Отличие состоит в том, что эта функция может выдать решение, не достигнув требуемой точности итераций. Это позволяет получить приближённое решение в случае, если функция Find не выдаёт решения. Следует иметь в виду, что при использовании функции Minerr необходимо обязательно проверять правильность решения системы уравнений.

Функции lsolve и Find позволяют получать решения символьным методом, результатом которого может быть численное решение или решение в аналитическом виде.

Решение систем уравнений матричным методом

Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных х₁, х₂, …, х_n:

Система линейных уравнений может быть записана в матричном виде:

Ах = b,

где:

.

Если det A  0 то система или эквивалентное ей матричное уравнение имеет единственное решение.

Решение систем уравнений с помощью функции Lsolve

Системы линейных уравнений удобно решать с помощью функции lsolve.

Функция lsolve(А, b) ‑ возвращает вектор решения x такой, что Ах = b.

Пример 5.1. Решение системы уравнений

Решение системы уравнений методом Гаусса

Метод Гаусса, его еще называют методом Гауссовых исключений, состоит в том, что систему уравнений приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей.

В матричной записи это означает, что сначала (прямой ход метода Гаусса) элементарными операциями над строками приводят расширенную матрицу системы к ступенчатому виду, а затем (обратный ход метода Гаусса) эту ступенчатую матрицу преобразуют так, чтобы в первых n столбцах получилась единичная матрица. Последний, (n + 1) столбец этой матрицы содержит решение системы.

В MathCAD прямой и обратный ходы метода Гаусса выполняет функция rref(A).

Пример 5.2. Решение системы уравнений методом Гаусса