Формула Торичелли

(2.6)

Из нее видно, что частицы жидкости, выходя из отверстия, имеют такую же скорость, какую они приобрели бы, свободно падая с высоты Н до уровня отверстия.

Течение вязких жидкостей в трубах

При тече­нии жидкости в трубах толщина этого слоя тем больше, чем больше вязкость жидкости, и возрастает по мере удаления от входа в трубу. В пределах пограничного слоя скорость жидкости возрастает от нулевой скорости на стенке трубы до макси­мального значения на внешней границе пограничного слоя. Таким образом, влияние вязкости приводит к тому, что скорость жидкости неодинакова в различных точках одного и того же поперечного сечения трубы. Распределение скорости жидкости в различных сечениях круглой цилиндрической трубы показано на рис.2.3.

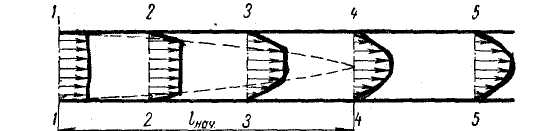
Рис.2.3.

Течение жидкости в трубах

Во входном сечении (1 - 1) толщина погра­ничного слоя равна нулю и скорость одинакова во всех точках этого сечения. По мере удаления от сече­ния 1 – 1 (сечения 2 - 2, 3 - 3) толщина пограничного слоя возрастает, и область потока с постоянной по се­чению скоростью уменьшается. Граница пограничного слоя показана на рис.2.3 пунктиром. В сечении 4 - 4 толщина пограничного слоя становится равной радиусу трубы, так что скорость оказывается различной во всех точках сечения, находящихся на неодинаковых рас­стояниях от оси трубы. Расстояние l_нач между сече­ниями 1 - 1 и 4 - 4 называется длиной участка гидро­динамической стабилизации.

Исследования показывают, что важнейшей характеристикой течения жидкостей является безразмерная величина Rе, которая называется числом Рейнольдса и для течения жидкости в круг­лой трубе равна:

(2.7)

где d - диаметр трубы, — средняя по сечению трубы скорость жидкости , V_сек - секундный объемный расход жид­кости, ρ и η - плотность и динамическая вязкость жидкости,  = η / ρ - кинематическая вязкость жидкости.

Переход ламинарного течения в турбулентное происходит при Rе> Rе_кр.

Величина Rе_кр зависит от ряда факторов: шерохо­ватости стенок трубы, способа осуществления ввода жидкости в трубу и т. д. Для гладких круглых труб Rе_кр ~ 2300.

Закон Ньютона для внутреннего трения

,

(2.8)

где - площадь внутренней поверхности слоя.

Формула Пуайзеля:

(2.9)

Соотношение используется для экспериментального определения коэффициента внутреннего трения жидкостей. При­меняемый для этого прибор - капиллярный вискозиметр.

Движение тел в жидкостях и газах

Вопрос о силовом взаимодействии между телом и набегаю­щим на него потоком жидкости или газа, а также о силах, дейст­вующих на тела, движущиеся в жидкости или газе, имеет большое практическое значение в самых разнообразных задачах гидро­аэродинамики.

В случае медленного движения небольшого шара в вязкой жидкости (Rе = , где и - скорость шара, d - его диаметр, v - кинематическая вязкость жидкости) справедлива фор­мула Стокса:

,

(2.10)

где r = d/2 - радиус шара.

Влияние сил внутреннего трения приводит также к измене­нию величины силы F_д. Это связано с тем, что при обтекании потоком вязкой жидкости тел с большой кривизной поверхности (например, тел шарообразной формы, поперечно обтекаемых круговых ци­линдров и т. п.) в хвостовой части тела возникает отрыв пограничного слоя от поверхности тела), приво­дящий к интенсивному вихреобразованию (рис.2.4).

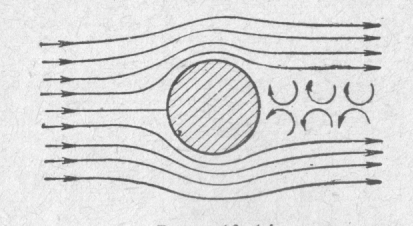
Рис. 2.4.

Обтекание тела потоком

В области поверх­ности тела, охваченной вихревым движением жидкости, давление ока­зывается пониженным по сравнению с соответствующим участком лобовой поверхности. Поэтому воз­никает результирующая сила F_д ≠ 0, направленная так же, как и сила F_тр, если тело симметрично.

В самом общем случае обтекания тела произвольной формы силу F, действующую на тело, можно разложить на две состав­ляющие: силу лобового сопротивления X, направленную вдоль скорости у_о набегающего потока, и подъемную силу У, направлен­ную перпендикулярно к V_о:

F = X + Y.

(2.11)

Сила лобового сопротивления может быть определена по формуле Ньютона:

,

(2.12)

где С_x - безразмерный коэффициент, называемый коэффициентом лобового сопротивления, S - площадь проекции тела па плоскость, перпендикулярную к вектору V_о (в случае крыла самолета под S понимается площадь поверхности крыла в плане).

Подъемная сила может быть определена по формуле, аналогич­ной (2.12):

(2.13)

где С_у - безразмерный коэффициент подъемной силы, кото­рый в основном зависит от формы тела и его ориентации по от­ношению к скорости набегаю­щего потока.

Подъемная сила может быть определена по формуле Жуковского:

Y = ρv0 z  Г

( 2.14)

где Г = - циркуляция вектора скорости жидкости вдоль контура L поперечного сечения тела.