2. Течение жидкостей и газов. Уравнение неразрывности и уравнение Бернулли Основные формулы

Раздел физики, в котором рассматриваются законы равновесия и движения жидких и газообразных тел, а также их взаимодействия с твердыми телами, называется гидроаэромеханикой.

Характерным свойством жидких и газообразных тел является их текучесть, то есть малая сопротивляемость деформации сдвига: если скорость сдвига стремится к нулю, то силы сопротивления жидкости или газа этой деформации также стремятся к нулю. Иными словами, жидкие и газообразные тела не обладают упру­гостью формы — они легко принимают форму того сосуда, в ко­тором находятся. Вследствие этого (закон Паскаля): внешнее давление, производимое на жидкость или газ, передается ими во все стороны равномерно.

Основным методом описания движения жидкости в гидро­аэродинамике является метод Эйлера, состоящий в задании за­висимости значений вектора υ скорости течения жидкости в раз­личных точках пространства от координат этих точек (х, у, z) и времени t:

υ = f (r, t)

(2.1)

или

υx = f1 (x, y, z, t) υy = f2 (x, y, z, t) υz = f3 (x, y, z, t)

(2.2)

где r = xi + yj + zk - радиус-вектор, проведенный из начала ко­ординат в рассматриваемую точку; i, j и k - единичные векторы (орты осей координат), υ_x, υ_y и υ_z - проекции вектора υ на оси координат.

Течение жидкости называется установившимся, или ста­ционарным, если скорость жидкости в каждой точке простран­ства, занятого жидкостью, не изменяется с течением времени, то есть υ не зависит от t: υ = f (r). В случае неустановившегося течения v зависит также и от времени t.

Рассмотрим участок элементарной струйки жидкости, огра­ниченной двумя произвольно выбранными нормальными сече­ниями 1 и 2, площади которых равны dS₁ и dS₂ (рис. 2.1).

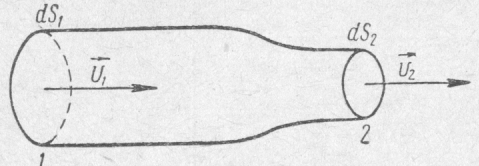
Рис. 2.1.

Участок элементарной струйки жидкости, огра­ниченной двумя произвольно выбранными нормальными сече­ниями 1 и 2, площади которых равны dS₁ и dS₂

Ско­рости жидкости в этих сечениях обозначим через v₁ и v₂. Если течение жидкости установившееся, то масса жидкости, заключенной в участке струи между сечениями 1 и 2, не зависит от времени. Следовательно, мас­са dm₁=ρ₁v₁ּdS₁ жидкости, поступающей в рассматриваемый участок за единицу времени сквозь сечение 1, равна массе dm₂ = ρ₂v₂ ּ dS₂ жидкости, вытекающей из этого участка за то же время сквозь сечение 2:

ρ1v1 ּdS1 = ρ1v2 ּdS2

(2.3)

Выделим мысленно часть идеальной несжимаемой жидкости, которая в некоторый момент времени t заполняет участок элемен­тарной струи, ограниченный нормальными сечениями 1 и 2 (рис.2.2).

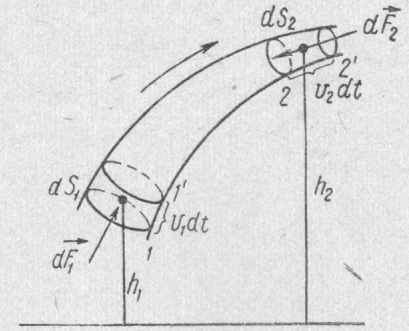
Рис. 2.2.

Элементарный участок струи, ограниченный нормальными сечениями 1 и 2

(2.4)

Это уравнение впервые было получено Д. Бернулли и назы­вается уравнением Бернулли. Оно, как видно из его вывода, является выражением закона сохранения энергии применительно к установившемуся течению идеальной несжимаемой жидкости.

В случае горизонтальной струи (например, при течении жидкости в горизонтальной трубе) величина h постоянна и урав­нение Бернулли принимает более простой вид:

(2.4‘)

Величина р называется статическим давлением, - скоростным, или динамическим, напором, а р₀ = р + — полным давлением.

Динамический напор равен:

=ρgΔH,

(2.5)

где ΔH — разность уровней жидкости в трубках а и Ь соответ­ственно полного и статического давлений.