Примеры решения задач

1.1. Может ли поле скоростей несжимаемой жидкости обладать потенциалом ?

Дано:	Решение: Потенциал скорости плоского потока несжимаемой жидкости удовлетворяет уравнению Лапласа:
		(1)

Проверим выполнение этого уравнения для заданного потенциала: , то есть поле скоростей несжимаемой жидкости может иметь такой потенциал.

1.2. При каком значении коэффициента а несжимаемой жидкости со следующими проекциями поля скоростей:

а) u_x = ax, u_у = aу;

б) u_x = 2ax, u_у = - 2aу.

Каков характер этих течений?

Дано: а) ux = ax, uу = aу; б) ux = 2ax, uу = - 2aу	Решение: При движении несжимаемой жидкости должно удовлетворяться уравнение неразрывноси . В первом случае а + а = 0, если а = 0. Следовательно, ux = 0, uу =0, то есть движение отсутствует.
а = ?

Во втором случае , , 2а – 2а = 0. Это условие выполняется при любом значении коэффициента а.

Чтобы определить характер течения, воспользуемся соотношениями (1.8), при которых ω_х = ω_у = 0, то есть течение потенциально

Эквипотенциальные линии – равнобокие гиперболы (асимптоты – биссектрисы углов между координатными осями.) Линии тока также равнобокие гиперболы (асимптоты – осей координат).

Форму линий тока (при а > 0) находим, проводя кривые, которые пересекают эквипотенциальные линии под прямым углом.

Задачи для самостоятельного решения

1. Поле скоростей газа задано проекциями Найти уравнение линий тока, а также траекторию частицы, которая проходит в момент времени t = 0 через точку пространства с координатами х = 2 и у = 4.

2. По заданным проекциям скоростей определить ускорение жидкой частицы в точке А с координатами х = 2 , у = 9, z = 3 в момент времени t = 2 с.

3. Найти уравнение семейства линий тока для плоского течения по заданным проекциям скоростей определить ускорение жидкой частицы в точке А с координатами х = 2 , у = 9, z = 3 в момент времени t = 2 с.

4. Пренебрегая сжимаемостью, определить на каком расстоянии от оси факела абсолютное давление газа должно стать равным , если окружная скорость на внешней границе на выходе из горелки 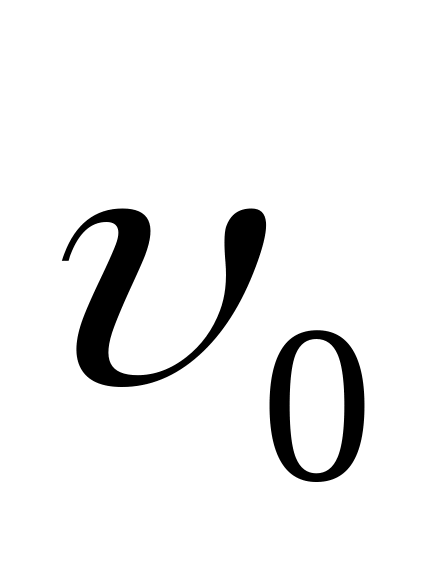= 20 м/с, разрежение в топке 98 Па, плотность газа 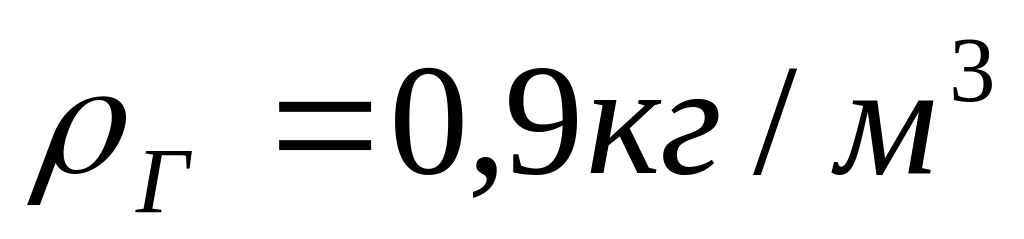, выходной диаметр горелки d = 0,5 м, атмосферное давление - нормальное.

5. Найти выражение для комплексного потенциала плоского источника, расположенного в начале координат. Определить скорость в точке z =3+4i.

6. С помощью функций 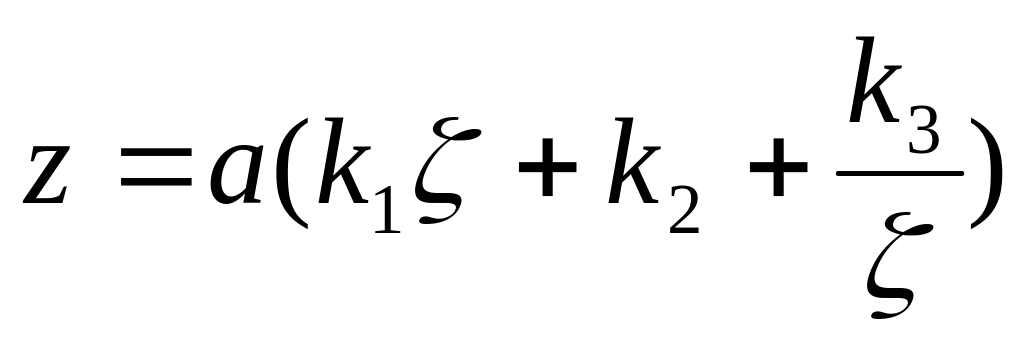отобразить отрезок прямой, совпадающей с осью х в плоскости z на плоскость . Построить результирующий контур, изобразить законы распределения скорости и коэффициента давления по контуру при движении жидкости вдоль оси х, если = 0,547, = 0,015, = 0,453.

7. Показать, что для движения, задаваемого проекциями скоростей , линии тока – это окружности.

8. Получить выражение для проекций локальных ускорений жидкой частицы, если уравнения движения имеют вид .

9. Определить ускорение жидкой частицы, если поле задано проекциями скоростей:

10. Определить ускорение жидкой частицы в точке пространства с координатами х = 3, у = 2, z = 1, если поле задано проекциями скоростей .

11. Движение несжимаемой жидкости задано проекциями скоростей . Установить вид выражения для проекции скорости на ось х, если в начале координат = 2.

12. Движение задано проекциями скоростей 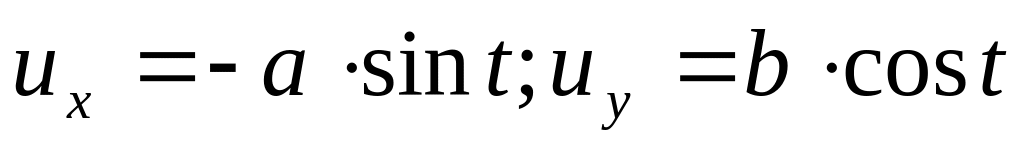. Найти уравнение линии тока, а также траекторию частицы, проходящую в момент времени t = 0 через точку пространства с координатами х = а, у = b.

13. Показать, что если поле задано проекциями скоростей , то линии тока представляют семейство гипербол. Получить уравнение траектории, проходящей в момент t = 0 через точку с координатами х = -1, у = -1. Построить линию тока и траекторию.

14. Определить расход жидкости, вытекающий через боковую поверхность цилиндра единичной толщины (z = 1), ось которого проходит через начало координат, если радиус цилиндра R = 0,1 м. Радиальную скорость течения считать постоянной и равной и = 3 м/с.

15. Проверить возможность существования движения несжимаемой жидкости для поля, заданного проекциями скоростей .

16. Доказать, что для поля, заданного проекциями скоростей , линии тока представляют собой окружности.

17. Определить скорость вращения жидкой частицы в точке пространства с координатами х = 3, у = 2, z =0, если поле задано проекциями скоростей

18. Получить выражение для линий тока, если проекции скоростей

1.19. Может ли поле скоростей несжимаемой жидкости обладать потенциалами, если

а) Если движение не потенциальное, найти выражения проекций скорости и построить соответствующие линии тока.

20. При каких значениях постоянных а, б, в, с возможны движения несжимаемой жидкости, если поля скоростей заданы выражениями: а) . Каков характер этих движений?