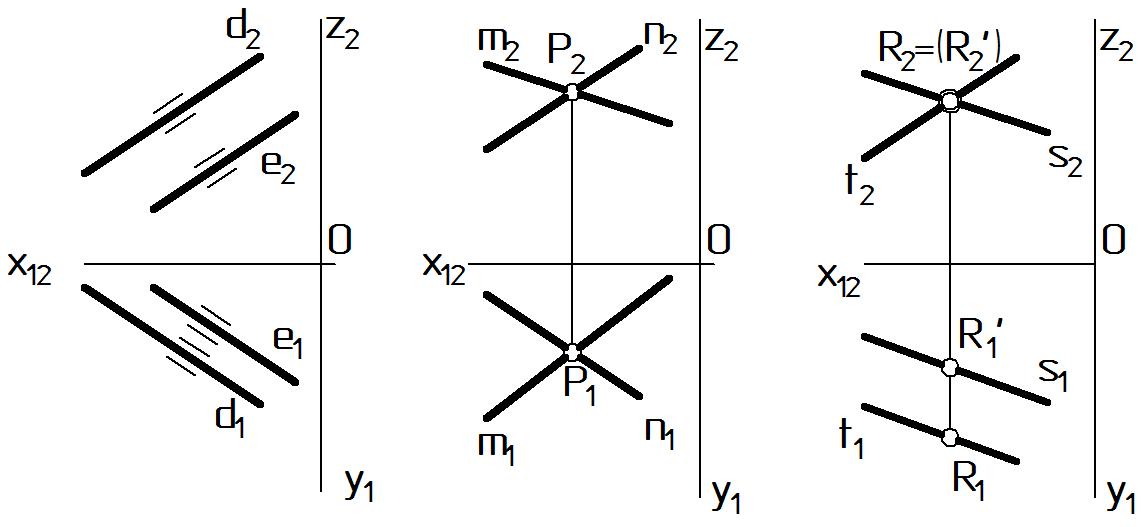
Метод конкурирующих точек

Метод конкурирующих точек предназначен для определения видимости проекций.

Конкурирующими называются точки, лежащие на одной проецирующей прямой. На одной из плоскостей проекции этих точек совпадают, что условно показывается двойной окружностью. Только одна из этих проекций видима (Рис. 15).

Метод конкурирующих точек: из двух совпадающих проекций конкурирующих точек, лежащих на одной

• горизонтально-проецирующей прямой, видна та, высота (z) которой больше;

• фронтально-проецирующей прямой, видна та, глубина (y) которой больше;

• профильно-проецирующей прямой, видна та, широта (x) которой больше.

Например, на рис. 15 а представлена пара конкурирующих точек G и H, принадлежащих горизонтально-проецирующей прямой а. На плоскости П₁ проекции точек совпадают G₁ = H₁. Посмотрим на П₂ высота какой точки больше? Для этого сравним координаты z проекций G₂ и H₂. z_G  z_H, то есть высота точки G больше, следовательно, G₁ видима. Скобки показывают, что проекция H₁ закрыта (невидима).

На рис. 15 б представлена пара конкурирующих точек I и K, принадлежащих фронтально-проецирующей прямой в. На плоскости П₂ проекции точек совпадают: I₂ = K₂. Посмотрим на П₁ глубина какой точки больше? Для этого сравним координаты y проекций I₁ и K₁. y_I  y_K, то есть глубина точки I больше, следовательно, I₂ видима. Скобки показывают, что проекция K₂ невидима.

На рис. 15 в представлена пара конкурирующих точек L и M, принадлежащих профильно-проецирующей прямой с. На плоскости П₃ проекции точек совпадают: L₃ = M₃. Посмотрим на П₁ или П₂ широта какой точки больше? Для этого сравним координаты x проекций I₁ и K₁. x_L  x_M, то есть широта точки L больше, следовательно, L₃ видима. Скобки показывают, что проекция M₃ невидима.

Взаимное положение прямых

По взаимному расположению двух прямых различают параллельные, пересекающиеся или скрещивающиеся прямые (Рис. 16).

При построении проекций параллельных прямых следует руководствоваться 4) инвариантным свойством проецирования: параллельные прямые проецируются в виде параллельных прямых: d // e  d₁ // e₁, d₂ // e₂ (Рис. 16 а).

При построении проекций пересекающихся прямых следует руководствоваться положением, вытекающим из 3) инвариантного свойства проецирования: если прямые пересекаются, то проекции точек пересечения их одноименных проекций лежат на общей линии связи: P = n  m  P₁ = n₁  m₁, P₂ = n₂  m² (Рис. 16 б).

Прямые скрещиваются, если они не параллельны и не пересекаются: s • t (Рис. 16 в). Отсюда следует, что такие прямые не имеют общей точки. На чертеже проекции точек инцидентных двум скрещивающимся прямым R  t и R’  s, могут совпадать только на одной из плоскостей, например, на плоскости П₂ проекции точек R и R’ совпадают. Такие точки являются конкурирующими точками.

а б в Рисунок 16

Проецирование плоскостей

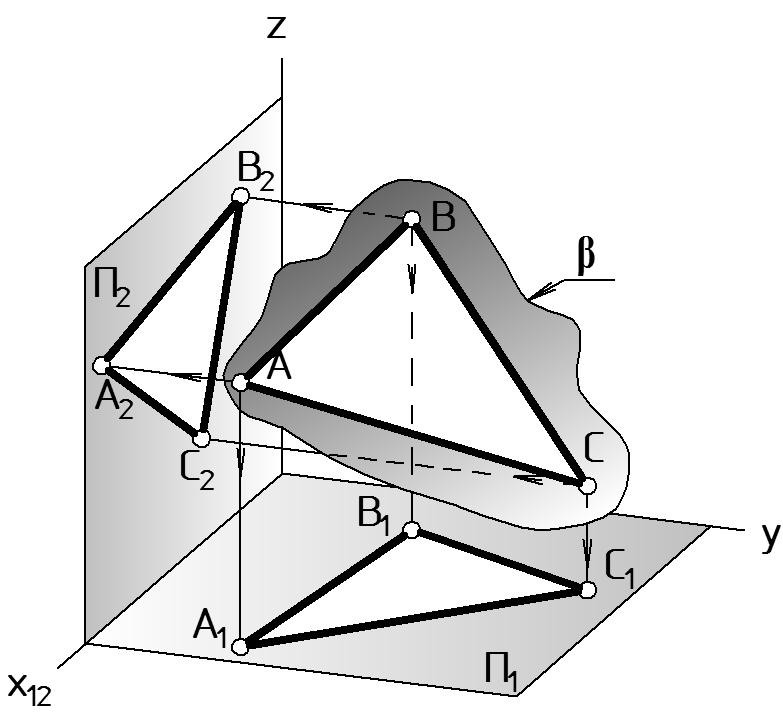
Плоскость - частный случай поверхности, через любые две точки которой проходит прямая, полностью принадлежащая этой поверхности. Плоскость бесконечна.

Рисунок 17

Положение плоскости в пространстве однозначно определяется тремя различными точками, не принадлежащими одной прямой (Рис. 17).

Плоскостями общего положения называются плоскости, наклоненные под произвольными углами к плоскостям проекций, т.е. они не параллельны и не перпендикулярны ни одной из основных плоскостей проекций.

На чертеже (Рис. 18) плоскость задают проекциями тех элементов, которыми она задана в пространстве, как правило, не показывая границ отсека плоскости (границы показаны для наглядности).

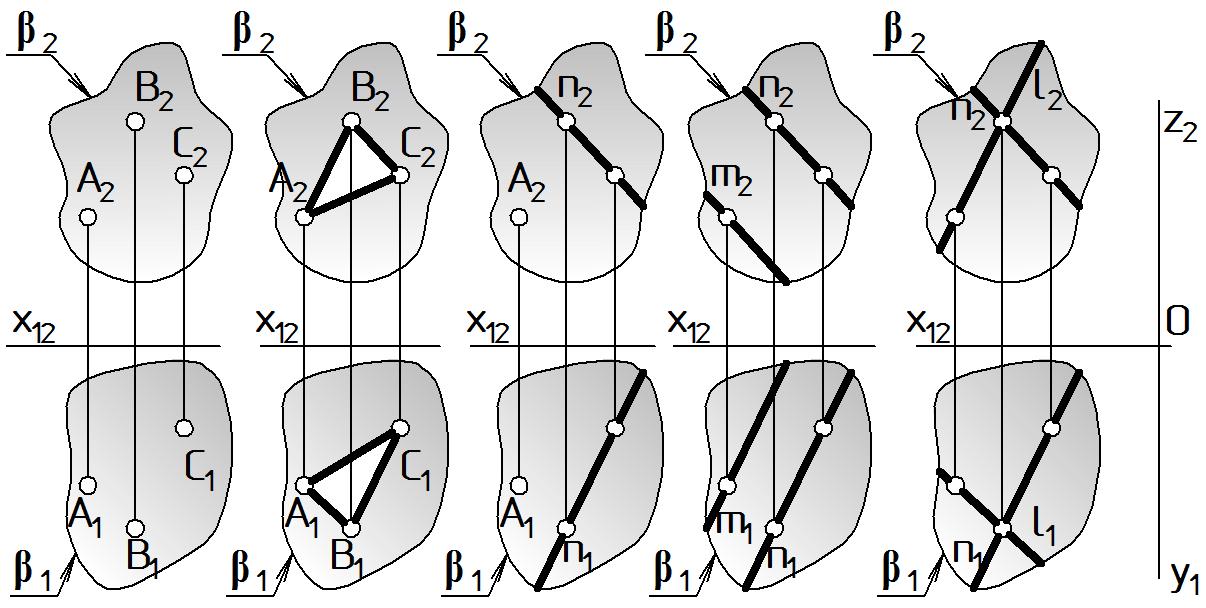
На чертеже плоскость можно задать различными определителями:

• тремя точками, не лежащими на одной прямой (Рис. 18 а);

• любой плоской фигурой, например, треугольником (Рис. 18 б);

• прямой и не принадлежащей ей точкой (Рис. 18 в);

• двумя параллельными прямыми (Рис. 18 г);

• двумя пересекающимися прямыми (Рис. 18 д).

 (А; В; С)  (АВС)  (А; n)  (m // n)  (l  n)

а б в г д

Рисунок 18

Все эти способы равноправны, и могут быть взаимно заменены. Например, если в плоскости  (m // n) (Рис. 18 г) взять точку А на прямой m, а В и С на прямой n, то способ представления параллельными прямыми будет заменен способом представления тремя точками  (А; В; С) (Рис. 18 а) и наоборот.

Замечание: если плоскость занимает общее положение, то ни одна из ее проекций не отображает истинной величины элементов плоскости.