Прямые частного положения

На рис. 10 изображена произвольная прямая общего положения. Дополнительно следует различать два класса прямых частного положения по типу параллельности и перпендикулярности по отношению к плоскостям проекций.

Первую группу составляют прямые уровня ‑ это прямые, параллельные одной из плоскостей проекций.

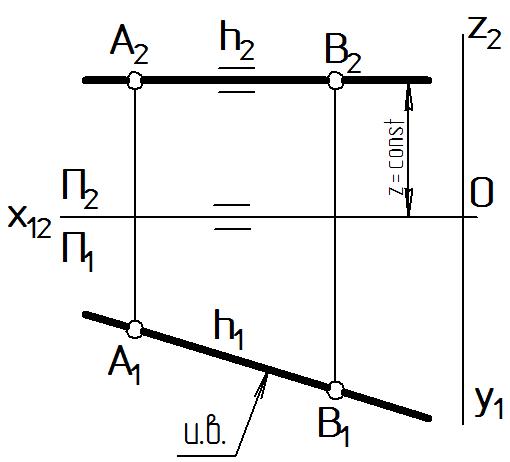
Рисунок 12

Горизонталь – прямая, параллельная горизонтальной плоскости проекций П₁, она обозначается традиционно h. На рис. 12 h  П₁.

На комплексном чертеже h₂  х₁₂, т.е. фронтальная проекция горизонтали h₂ – это горизонтальная линия на чертеже, параллельная оси х₁₂, так как высота любой точки горизонтали есть величина постоянная: z = const.

Горизонтальная проекция горизонтали h₁ имеет произвольный угол наклона к координатным осям, а ее отрезок изображается на П₁ в истинную величину:

A₁B₁= и.в.AB.

Фронталь – прямая, параллельная фронтальной плоскости проекций П₂, она обозначается f. На рис. 13 f  П₂.

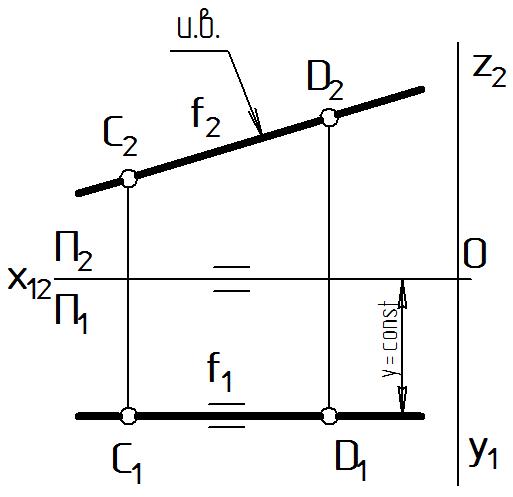
Рисунок 13

На комплексном чертеже f₁  х₁₂, т.е. горизонтальная проекция фронтали f₁ – это горизонтальная линия на чертеже, параллельная оси х₁₂, так как глубина любой точки фронтали есть величина постоянная: y = const.

Фронтальная проекция фронтали f₂ имеет произвольный угол наклона к координатным осям, а ее отрезок изображается на П₂ в истинную величину: С₂D₂= и.в.CD.

Профильная прямая – прямая, параллельная профильной плоскости проекций П₃, она обозначается p.

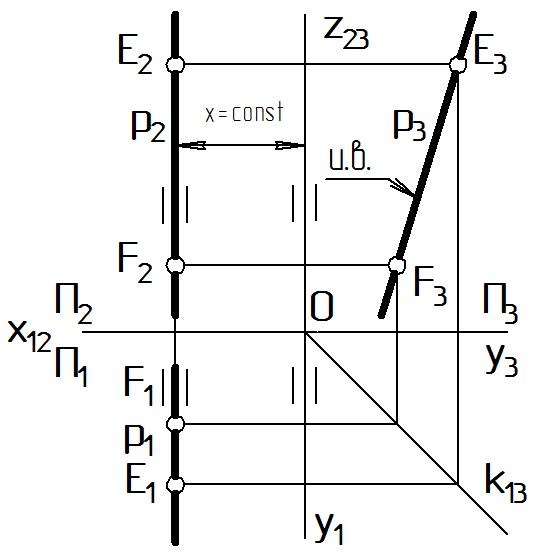
Рисунок 14

На рис. 14 p  П_3. На комплексном чертеже р₂ и р₁ – прямые, параллельные осям р₁  y₁, р₂  z₂₃, так как широта любой точки прямой величина постоянная: х = const.

Паре прямых р₂ и р₁, совпадающих с вертикальной линией связи, соответствует в пространстве бесчисленное множество прямых, параллельных П₃. Поэтому каждая профильная прямая задается двумя точками или применяется трехкартинный чертеж.

Профильная проекция профильной прямой р₃ имеет произвольный угол наклона к координатным осям, а ее отрезок изображается на П₃ в истинную величину: E₃F₃= и.в.EF.

Вторую группу составляют проецирующие прямые ‑ это прямые, перпендикулярные какой-либо плоскости проекций.

Одна из проекций этих прямых вырождена в точку. Две другие проекции отрезка прямой изображаются в истинную величину. Заметим, что проецирующее положение прямой является более сильным, чем положение линии уровня, так как при проецирующем положении прямая остается параллельной сразу двум плоскостям, например, если прямая перпендикулярна плоскости П₃, то она параллельна плоскостям П₁ и П₂, следовательно обладает свойствами горизонтали и фронтали одновременно.

Горизонтально-проецирующая прямая ‑ прямая, перпендикулярная П₁.

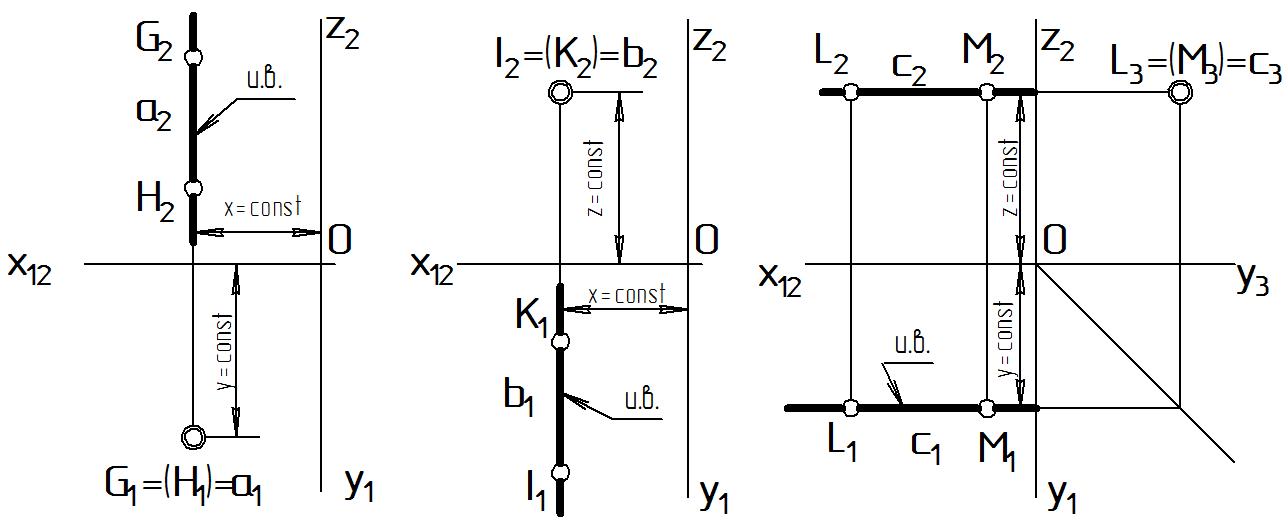
На рис. 15 а а  П₁. На плоскости П₁ проекции задающих эту прямую точек совпадают: G₁ = (H₁). Так как прямая а параллельна одновременно плоскостям П₂ и П_3, то она является фронталью и профильной прямой одновременно. Глубина и широта любой точки этой прямой есть величина постоянная: х = const, y = const.

Фронтально-проецирующая прямая ‑ прямая, перпендикулярная П₂.

На рис. 15 б b  П₂. На плоскости П₂ проекции задающих эту прямую точек совпадают: I₂ = (K₂). Так как прямая параллельна одновременно плоскостям П₁ и П_3, то она является горизонталью и профильной прямой одновременно. Высота и широта любой точки этой прямой есть величина постоянная: х = const, z = const.

Профильно-проецирующая прямая ‑ прямая, перпендикулярная П₃.

На рис. 15 в с  П₃. На плоскости П₃ проекции задающих эту прямую точек совпадают: L₃ = (M₃). Она является горизонталью и фронталью одновременно. Высота и глубина любой точки этой прямой есть величина постоянная: y = const, z = const.

а б в Рисунок 15