Построение проекций точки по координатам

При построении ортогональных проекций точки следует руководствоваться инвариантным свойством ортогонального проецирования 1): проекция точки – это точка.

Простейшим способом определения местоположения точки в трехмерном пространстве при использовании в качестве системы отсчета декартовой системы координат является вычисление трех ее координат.

Рассмотрим пример. Пусть требуется построить чертеж точки А, расположение которой определяется ее координатами: x_А = 70, y_А = 30, z_А = 45. На чертеже координаты точки обычно задаются в тех единицах измерения, которые выбраны для создания всего изображения. Чаще всего это миллиметры (мм). Более сокращенная запись выглядит следующим образом: А (70; 20; 45).

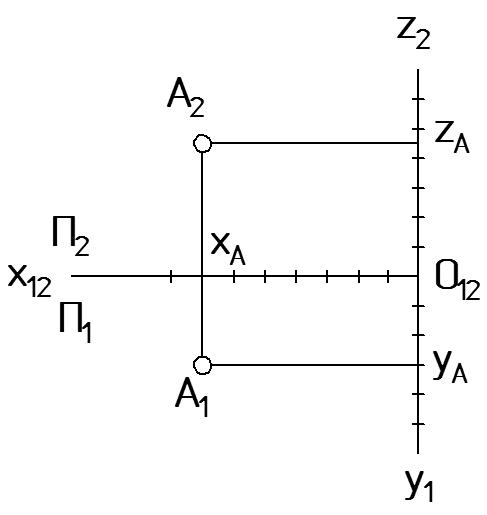
Построим точку А на двухкартинном комплексном чертеже (Рис. 9 а). Точка определена на комплексном чертеже тогда и только тогда, когда заданы две ее проекции ‑ горизонтальная и фронтальная. Следовательно, необходимо построить горизонтальную проекцию А₁ и фронтальную проекцию А₂.

Горизонтальная плоскость проекций П₁ определяется осями x₁ и y₁, а фронтальная П₂ – x₂ и z₂. Следовательно, А₁ определяется координатами x_А = 70 и y_А = 30, а А₂ ‑ координатами x_А = 70 и z_А = 45. Заданные координаты откладываются на соответствующих (заранее проградуированных в заданном масштабе) осях. Искомая проекция точки находится в пересечении прямых, проведенных параллельно осям проекций.

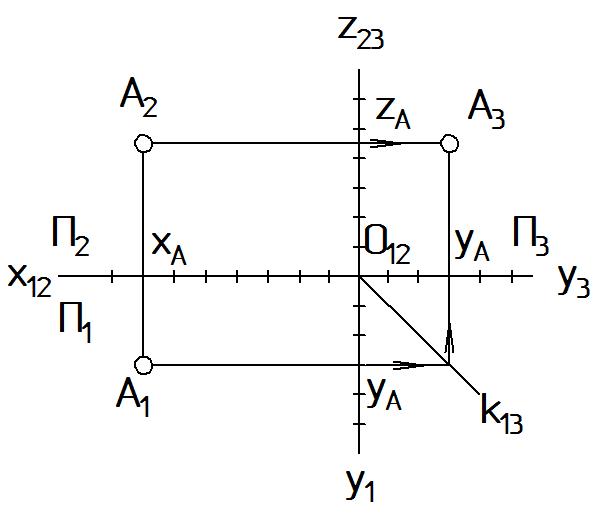
Если требуется построить трехкартинный комплексный чертеж, то, продолжая тот же метод для построения проекции А₃, нужно отложить координаты y_А = 30 и z_А = 45 на осях у₃ и z₃₂, определяющих профильную плоскость проекций П₃.

а б

Рисунок 9

Однако можно использовать графический метод без откладывания координат (Рис. 9 б). Для этого необходимо провести горизонтальную линию связи от точки А₂ и ломаную линию связи от точки А₁, причем ломаться линия должна на постоянной прямой комплексного чертежа к₁₃. В месте пересечения линий связи будет А₃.

Проецирование прямой

В пространстве прямая может быть задана двумя точками, точкой и направлением или линией пересечения двух плоскостей. Прямая бесконечна.

При построении проекции прямой следует исходить из инвариантного свойства ортогонального проецирования 2): проекция прямой – это прямая, за исключением случая вырождения ее в точку при расположении прямой параллельно направлению проецирования:

При изображении прямых на чертеже обычно строятся проекции фрагмента прямой с указанием двух определяющих точек.

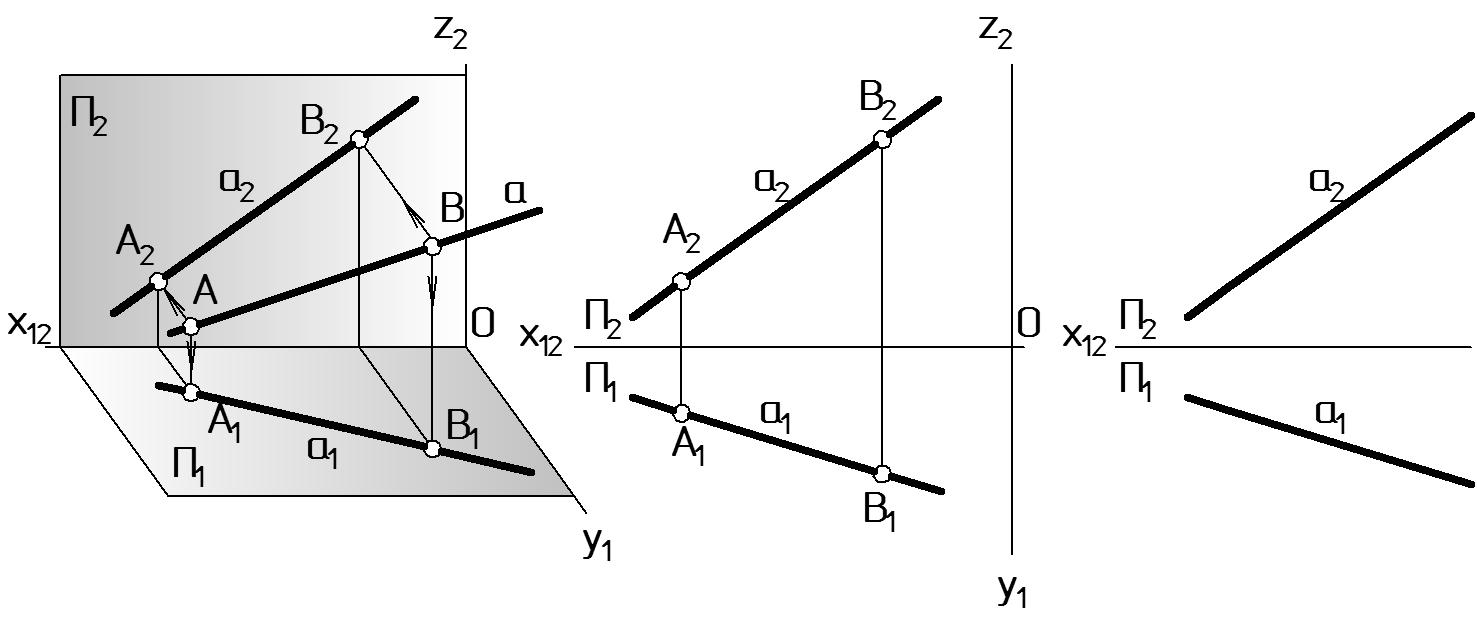
На рис. 10 а показана прямая а (А; В), не перпендикулярная и не параллельная ни одной плоскости проекций – это прямая общего положения.

На комплексном чертеже проекции прямой общего положения произвольно наклонены (углы наклона к координатным осям — произвольные, но отличные от 0 и 90°). На рис. 10 б а₁ — горизонтальная, а₂ — фронтальная проекция прямой а.

Можно изображать проекции фрагмента прямой без указания задающих точек (Рис. 10 в).

а б в

Рисунок 10

Рассмотрим вопрос об инцидентности точки прямой линии. При этом следует исходить из инвариантного свойства проецирования 3): если точка инцидентна (принадлежит) прямой в оригинале, то и проекция точки инцидентна одноименной проекции прямой на любой плоскости проекций.

Действительно (Рис. 10 а и 10 б), любая точка на прямой а будет проецироваться на П₂ таким образом, что она обязательно попадет на проекцию прямой а₂. Для точек А и В эти проекции показаны (А₂ и В₂). И, соответственно, любая точка на прямой а будет проецироваться на П₁ таким образом, что она обязательно попадет на проекцию прямой а₁. Для точек А и В эти проекции показаны (А₁ и В₁).

Принадлежности точки прямой только на фронтальной, либо только на горизонтальной проекции не достаточно. Любая точка, лежащая на проецирующей прямой перед, за, над или под прямой, будет обладать единственным совпадением проекций точки и прямой, но отсутствием совпадения оригиналов.

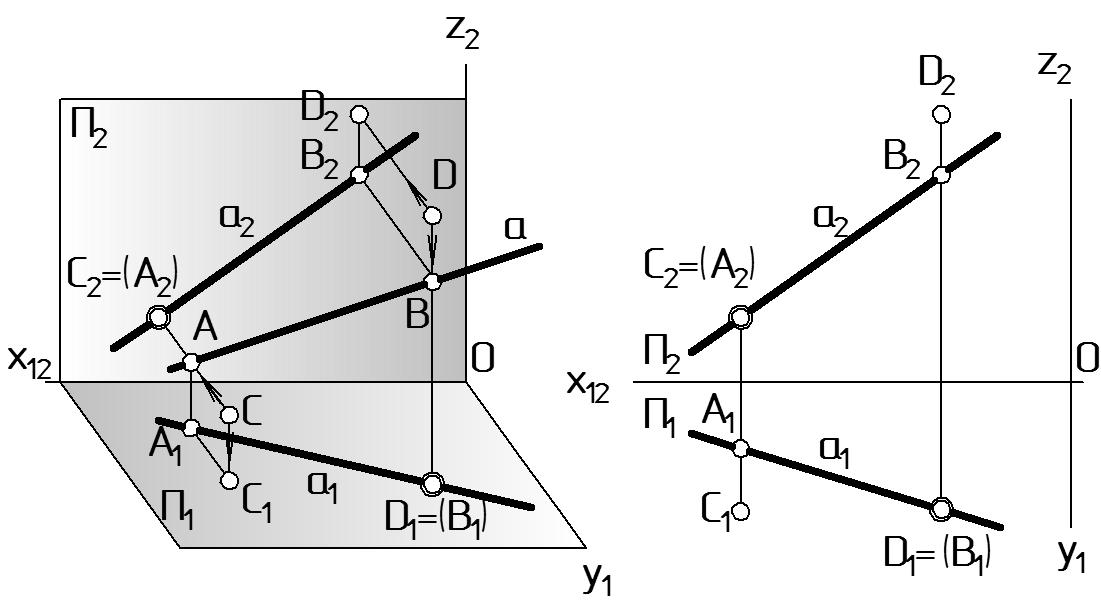
Например, на рис. 11 а и 11 б показана точка С, расположенная в пространстве перед прямой а (А; В). На П₂ проекция C₂ совпадает с проекцией А₂: C₂ = (А₂). Это условно показано двойной окружностью. Скобки в обозначении показывают, что проекция А₂ закрыта проекцией C₂ (невидима). На П₁ проекция C₁ не совпадает с проекцией А₁, хотя и находится на одной линии связи.

На этом же рис. 11 а и 11 б показана точка D, расположенная в пространстве над прямой а (А; В). На П₂ проекция D₂ не совпадает с проекцией B₂. На плоскости П₁ проекция D₁ совпадает с проекцией B₁: D₁ = (B₁). Скобки показывают, что проекция B₁ невидима.

а б Рисунок 11

Отсюда можно сделать вывод, что вопрос об инцидентности точки прямой линии необходимо решать на двухкартинном чертеже.