Проецирование точки на 3 плоскости проекций

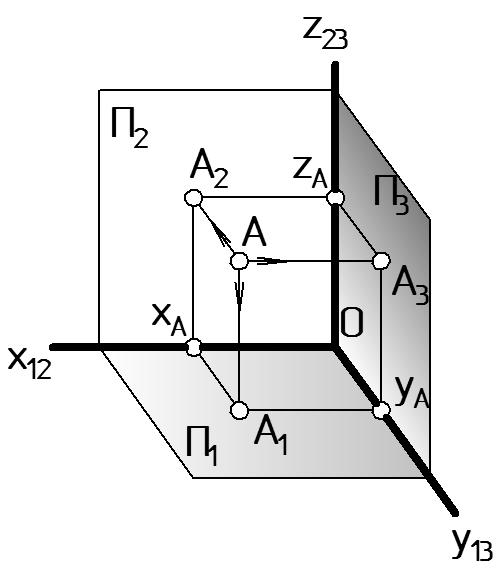
В некоторых случаях для полной характеристики формы объекта двух его проекций недостаточно. Поэтому иногда проецирование ведется на три взаимно-перпендикулярные плоскости П₁, П₂ и П₃. Плоскость П₃ называется профильной плоскостью проекций. Эти плоскости образуют в пространстве прямоугольный трехгранник с ребрами х₁₂, y₁₃, z₂₃ (Рис. 7).

Рисунок 7

А₁ – горизонтальная проекция точки A: А₁ = АА₁  П₁. Горизонтально-проецирующая прямая АА₁ перпендикулярна П₁. Отрезок AA₁ определяет координату z точки А, т.е. ее высоту.

А₂ – фронтальная проекция точки A: А₂ = АА₂  П₂. Фронтально-проецирующая прямая АА₂ перпендикулярна П₂. Отрезок AA₂ определяет координату у точки А, т.е. ее глубину.

А₃ – профильная проекция точки A: А₃ = АА₃  П₃. Прямая АА₃ перпендикулярна П₃, она называется профильно-проецирующей прямой. Отрезок AA₃ определяет координату х точки А, т.е. ее широту.

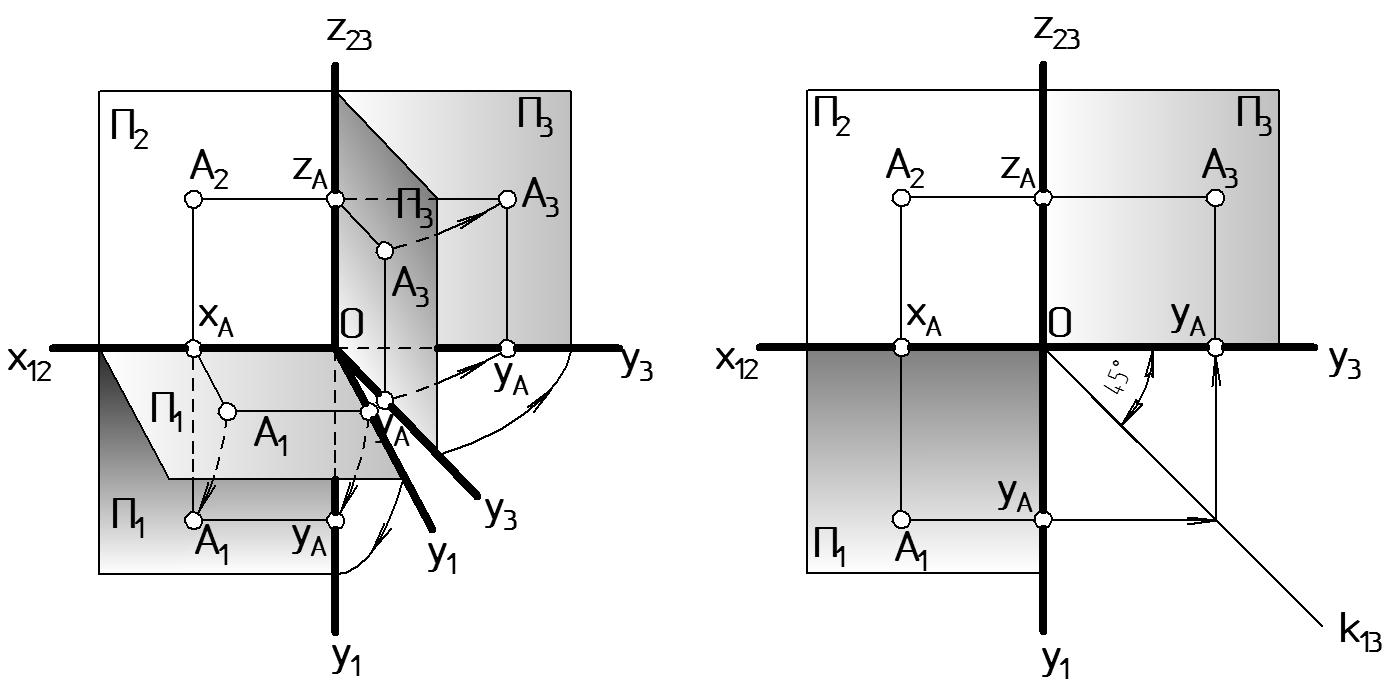
Чтобы получить трехкартинный комплексный чертеж после проецирования точки одновременно осуществляют два вращения (Рис. 8 a):

• плоскость П₁ вращается вокруг оси х₁₂ по часовой стрелке на 90 до совмещения ее с плоскостью П₂, что полностью соответствует получению двухкартинного чертежа;

• плоскость П₃ вращается вокруг оси z₂₃ против часовой стрелки на 90, если смотреть с конца оси z₂₃, до совмещения ее с плоскостью П₂.

а б

Рисунок 8

На рис. 8 б показан полученный таким образом трехкартинный комплексный чертеж точки А.

Очевидно, что разворот двух плоскостей П₁ и П₃ не возможен без дублирования оси y₁₃. Одна из осей y₁ будет участвовать в повороте плоскости П₁, а вторая y₃ – П₃. Но эта условность должна обеспечивать одинаковую величину глубины точки, т.е. у₁ = у₃.

Одним из графических методов, обеспечивающих эту возможность, является способ, показанный на рис. 8 б. Между осями у₁ и у₃ проведем биссектрису к₁₃, называемую постоянной прямой комплексного чертежа. Линию связи, соединяющую горизонтальную проекцию А₁ с профильной А₃, будем преломлять под прямым углом на этой прямой. Горизонтальный участок А₁y_А  у₁, а вертикальный А₃y_А  у₃.

По аналогии с двухкартинным чертежом можно доказать, что линии связи проекций точек будут перпендикулярны соответствующим осям, т.е. A₁A₂  х₁₂, A₂A₃  z₂₃.

На рис. 8 б: А₁А₂ ‑ вертикальная линия связи;

А₂А₃ ‑ горизонтальная линия связи;

А₁y_A и y_AА₃ ‑ ломаная линия связи;

Ox_А = y_АА₁ = z_АА₂ = х ‑ широта точки А;

Oy_А = x_АА₁ = z_АА₃ = y ‑ глубина точки А;

Oz_А = x_АА₂ = y_АА₃ = z ‑ высота точки А.

Замечание: так как плоскости не имеют границ, в совмещенном положении (на эпюре) границы их не показывают. Оси проекций фиксируют положение плоскостей проекций. Часто практически гораздо важнее установить взаимное расположение элементов оригинала (т. е. изображаемого предмета) и их форму, чем расстояния до плоскостей проекций. Поэтому, при выполнении чертежей в этих случаях оси проекций могут не изображаться или изображаться частично, подразумевая, однако, что проецирование ведется ортогональное на две или три взаимно-перпендикулярные плоскости. Линии связи при этом изображаются обязательно. Если по какой-либо причине на чертеже требуется восстановить опущенные оси проекций, то их можно провести, ориентируясь на линии связи проекций точки так, что бы х₁₂  A₁A₂, z₂₃ . A₂A₃, а начало координат располагалось на постоянной прямой к₁₃.