Комплексные чертежи Проецирование точки на 2 плоскости проекций

Рисунок 4

Рассмотрим систему двух взаимно-перпендикулярных плоскостей П₁ и П₂ (Рис. 4).

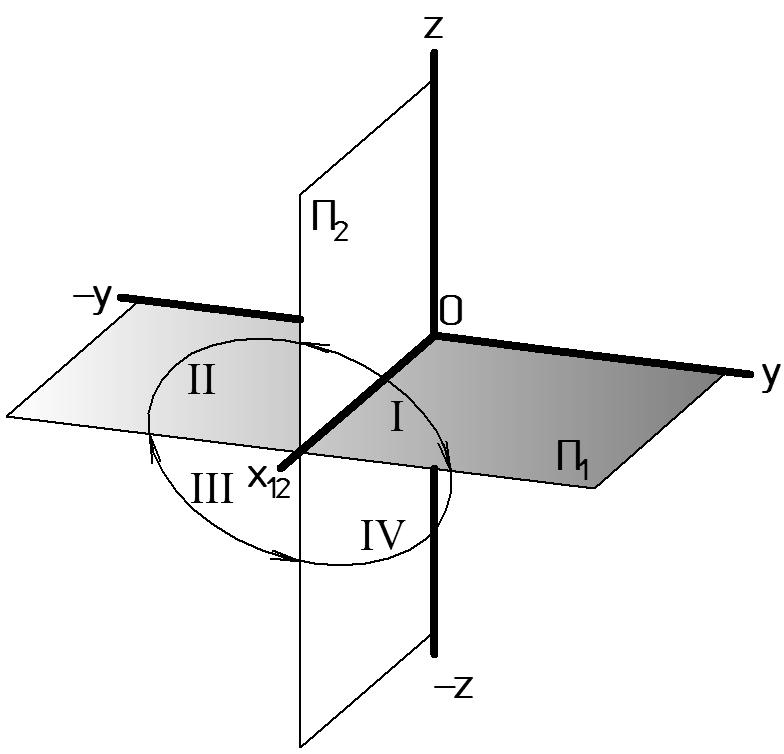
Плоскость П₁ (xOy) назовем горизонтальной плоскостью проекций, П₂ (xOz) – фронтальной плоскостью проекций.

Линия пересечения плоскостей П₁ и П₂ – ось проекций х₁₂ .

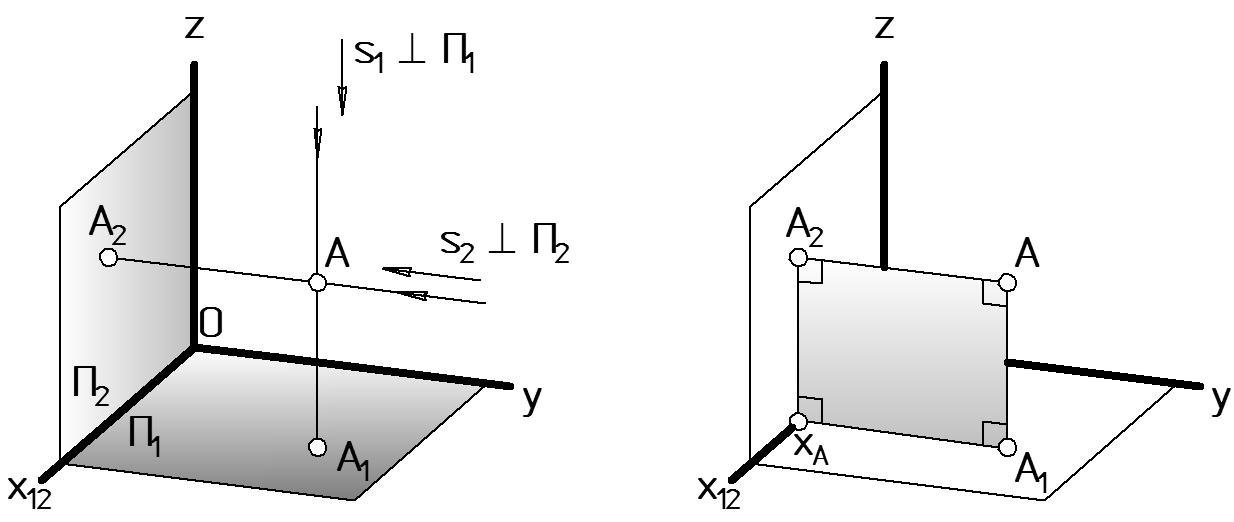
Две плоскости проекций П₁ и П₂ делят все пространство на четыре части, называемые четвертями. Нумерация четвертей указана на рис. 4 римскими цифрами. Рассмотрим I четверть пространства, в которой координатные оси имеют положительные направления (Рис. 5 а).

Спроецируем ортогонально точку А на обе плоскости проекций, т.е. опустим из этой точки проецирующие перпендикулярные прямые AA₁ и AA₂ на плоскости П₁ и П₂ соответственно.

а б

Рисунок 5

А₁ – горизонтальная проекция точки A: А₁ = АА₁  П₁. Прямая АА₁ перпендикулярна П₁, она называется горизонтально-проецирующей прямой. Отрезок AA₁ определяет координату z точки А, т.е. ее высоту.

А₂ – фронтальная проекция точки A: А₂ = АА₂  П₂. Прямая АА₂ перпендикулярна П₂, она называется фронтально-проецирующей прямой. Отрезок AA₂ определяет координату у точки А, т.е. ее глубину.

Рассмотрим фигуру АА₂x_AА₁ (Рис. 5 б). А – прямой, так как его стороны перпендикулярны к взаимно перпендикулярным плоскостям П₁ и П₂. А₁ и А₂ – прямые по условию ортогонального проецирования. Сумма внутренних углов любого четырехугольника составляет 360. Следовательно x_А тоже прямой, а фигура АА₂x_AА₁ – прямоугольник. Тогда: AА₁ = А₂x_A = z ‑ высота точки А, AA₂ = A₁x_A = y ‑ глубина точки А.

Так как AA₁  П₁ и AA₂  П₂, то плоскость, в которой лежит прямоугольник АА₂x_AА₁, перпендикулярна к плоскостям П₁ и П₂, на основании теоремы о перпендикулярных плоскостях. Напомним эту теорему: плоскости перпендикулярны, если одна из них проходит через прямую, которая перпендикулярна к другой плоскости. Следовательно, плоскость АА₂x_AА₁ перпендикулярна к линии пересечения П₁ и П₂ ‑ оси х₁₂. Плоскость АА₂x_AА₁ пересекает плоскость П₁ по прямой А₁х₁₂, а плоскость П₂ ‑ по прямой А₂х₁₂. Эти прямые также перпендикулярны к оси х₁₂, как прямые, лежащие в плоскости АА₂x_AА₁.

а б

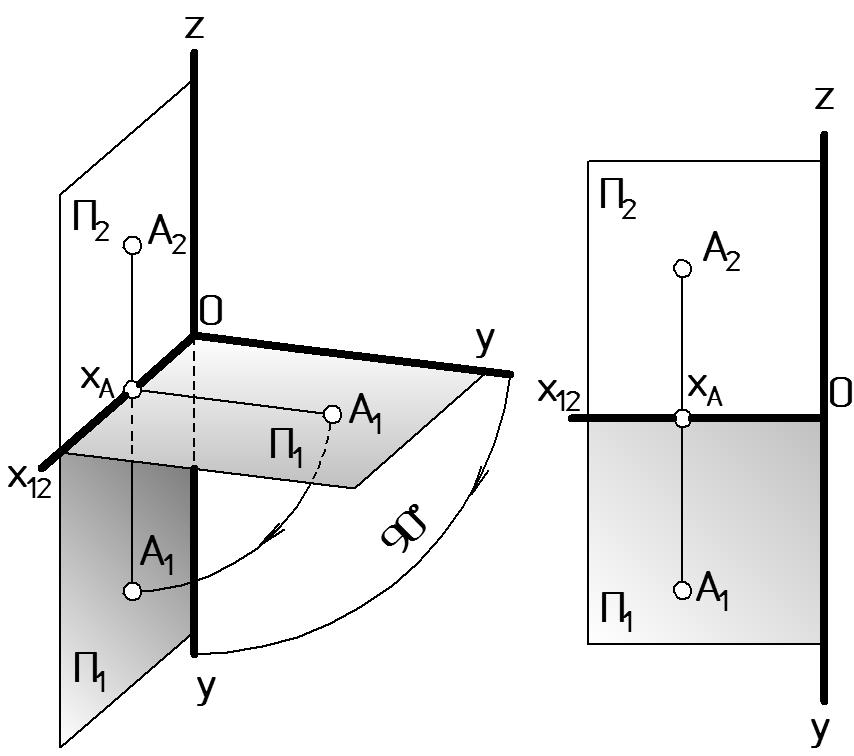
Рисунок 6

Повернем плоскость П₁ на 90° вокруг оси х₁₂ по часовой стрелке, если смотреть слева, тем самым совместим ее с плоскостью П₂ (Рис. 6 а).

Чертеж, полученный на двух совмещенных плоскостях проекций, т.е. включающий две проекции объекта, называется двухкартинным комплексным или эпюром (Рис. 6 б).

Как доказано выше A₁x_A  х₁₂ и А₂x_A  х₁₂, следовательно A₁A₂  х₁₂. Таким образом, на эпюре две проекции A₁ и A₂ точки А располагаются на общей линии связи, перпендикулярной к оси х₁₂.

Замечание: при выполнении двухкартинного комплексного чертежа необходимо показывать линии связи проекций тонкими линиями, только при их наличии можно установить проекционную связь точек изображения. Допустимо использовать неполный вариант, включающий начало и конец линии связи. Точку пересечения линии связи с осью х₁₂ не обозначают.

Комплексный чертеж (эпюр) является обратимым, так как по двум проекциям точки, расположенных на общей линии связи, можно определить ее положение в пространстве относительно выбранной системы координат. Действительно (Рис. 6 б), [A₁x_A] = y ‑ глубина точки А, [А₂x_A] = z ‑ высота точки А, [Oх_А] = x ‑ широта точки А.