Введение Задачи начертательной геометрии

Зародившись в глубокой древности, различные способы изображений по мере развития материальной жизни общества претерпевали глубокие изменения. От примитивных изображений, передававших геометрические формы изображаемых на них объектов весьма приближенно, постепенно совершился переход к составлению проекционных чертежей, отражающих геометрические свойства изображаемых на них объектов.

Создание начертательной геометрии в конце 18 века связывают с именем французского инженера и математика Гаспара Монжа (1746-1818). Он впервые разрешил основные теоретические проблемы метрически полных изображений, тем, что он ортогонально (прямоугольно) спроецировал трехмерную геометрическую форму на две взаимно перпендикулярные плоскости проекций и совместил оба изображения.

Начертательная геометрия как учебная дисциплина занимается двумя основными вопросами:

1) изучением методов построения плоских изображений (чертежей) пространственных геометрических объектов.

2) изучением пространственных геометрических объектов по их плоским изображениям (чертежам).

Чертеж, применяемый в технике, должен быть:

1) обратимым, т. е. давать возможность решения задачи о восстановлении формы и положения объекта в пространстве по изображению;

2) наглядным,

3) простым и точным по выполнению.

Для выполнения этих требований чертеж должен быть построен по определенным геометрическим правилам. Геометрически закономерные изображения получаются при помощи операции проецирования. Получающиеся при этом изображения называются проекционными чертежами.

Методы проецирования

Любую геометрическую фигуру можно рассматривать как множество принадлежащих ей точек.

Сущность операции проецирования состоит в проведении через точку оригинала прямой линии, которая называется проецирующей прямой (Рис. 1). В результате пересечения проецирующей прямой с какой-либо плоскостью проекций П_i, получают изображение, называемое проекцией.

Проецирующие прямые можно провести несколькими способами. В зависимости от этого различают:

• центральное проецирование (Рис. 1 а), когда все проецирующие прямые проходят через точку S, называемую центром проекций;

• параллельное проецирование, когда все проецирующие прямые параллельны между собой и образуют одинаковый угол с плоскостью проекций П_i (Рис. 1 б). Параллельное проецирование можно считать частным случаем центрального, когда центр проекций S отнесен в бесконечность.

• ортогональное (от orthogonios (лат.) – прямоугольный) проецирование, частный случай параллельного, когда все проецирующие прямые образуют прямой угол с плоскостью проекций П_i (Рис. 1 в).

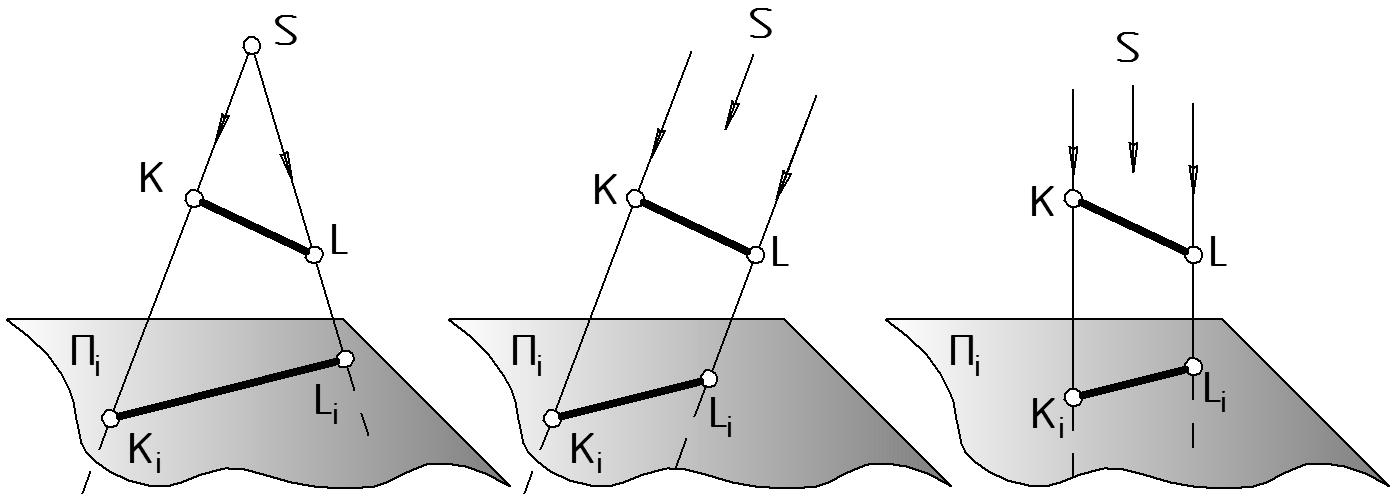
а б в

Рисунок 1

Свойства операции проецирования

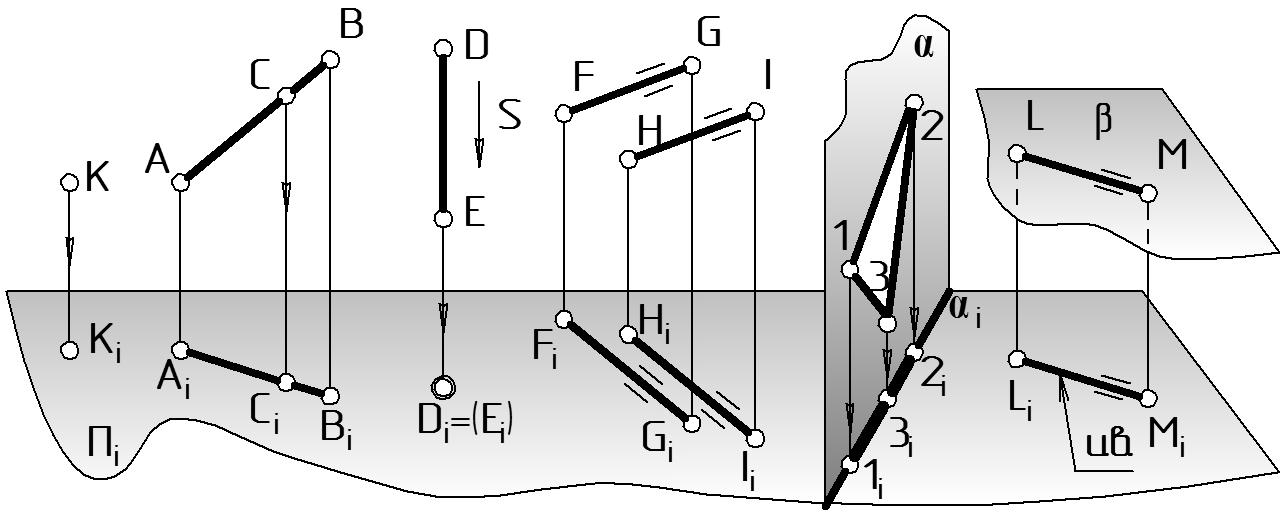
Геометрические характеристики оригинала при проведении операции проецирования могут изменяться или оставаться неизменными. Не искажающиеся свойства называют инвариантами проецирования.

Инварианты, правомерные для любого вида проецирования, состоят в следующем:

1. проекция точки – это точка: К  К_i (Рис. 2 а);

2. проекция прямой – это прямая: АВ  А_iВ_i (Рис. 2 б), за исключением случая вырождения в точку при расположении прямой параллельно направлению проецирования: DE // s, DE  D_i = (E_i) (Рис. 2 в);

3. если точка инцидентна (принадлежит) прямой в оригинале, то и проекция точки инцидентна одноименной проекции прямой на любой плоскости проекций: C  АВ  C_i  А_iВ_i, C_j  А_jВ_j (Рис. 2 б).

Инварианты, характерные для параллельного и ортогонального проецирования, состоят в следующем:

4. параллельные прямые проецируются в виде параллельных прямых: FG // HI  F_iG_i // H_iI_i, F_jG_j // H_jI_j (Рис. 2 г);

5. отношение отрезков, лежащих на параллельных прямых (или на одной прямой), сохраняется: FG // HI  FG / HI = F₁G₁ / H₁I₁ (Рис. 2 г) (или C  АВ  АС / СВ = А_iС_i / С_iВ_i (Рис. 2 б).

6. если фигура принадлежит плоскости , перпендикулярной плоскости проекций П_i, то проекция фигуры полностью совпадает со следом плоскости _i (след плоскости – это линия пересечения плоскости  с плоскостью П_i: _i  =   П_i): 123  ,   П_i  (1_i; 2_i; 3_i)  _i (Рис. 2 д).

Для ортогонального проецирования можно выделить еще дополнительный инвариант:

7. если фигура принадлежит плоскости , параллельной плоскости проекций П_i, то проекция на П_i равна истинной величине фигуры: LM  ,  // П_i  L_iM_i = и.в. LM (Рис. 2 е).

а б в г д е

Рисунок 2

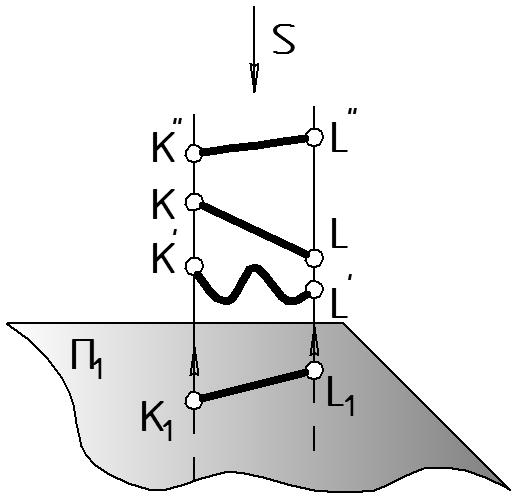
Рисунок 3

Изображения, полученные с помощью рассмотренных выше методов проецирования с использованием указанных инвариантов, позволяют решать прямую задачу — по данному оригиналу однозначно строить его проекцию.

Обратная задача — восстановление оригинала по его изображению — не решается однозначно. Например (Рис. 3), одной проекции линии К₁L₁ может соответствовать множество линий KL, K’L’,…, отличающихся формой и положением в пространстве.

Из рис. 3 следует, что изображение, представленное одной проекцией, не является обратимым.

Для получения обратимых чертежей нужны дополнительные условия. Например, оригинал проецируют прямоугольно (ортогонально) на две или три взаимно-перпендикулярные плоскости проекций. В этом случае чертежи называют комплексными двухкартинными или трехкартинными. Они нашли наибольшее применение в технике и строительстве.