7.Построение развертки многогранника

Разверткой многограника называется плоская фигура, образованная последовательным совмещением всех граней поверхности с одной плоскостью без складок и разрывов.

Так как грани многогранной поверхности изображаются на развертке в истинную величину, то построение сводится к определению истинной величины граней поверхности – плоских многоугольников.

Развертка пирамиды осуществляется методом триангуляции (построения треугольников) в следующем порядке:

1. определяют истинную величину всех ребер пирамиды;

2. определяют истинную величину основания пирамиды;

3. по найденным трем сторонам строят какую-либо боковую грань, затем пристраивают к ней все остальные грани и основание.

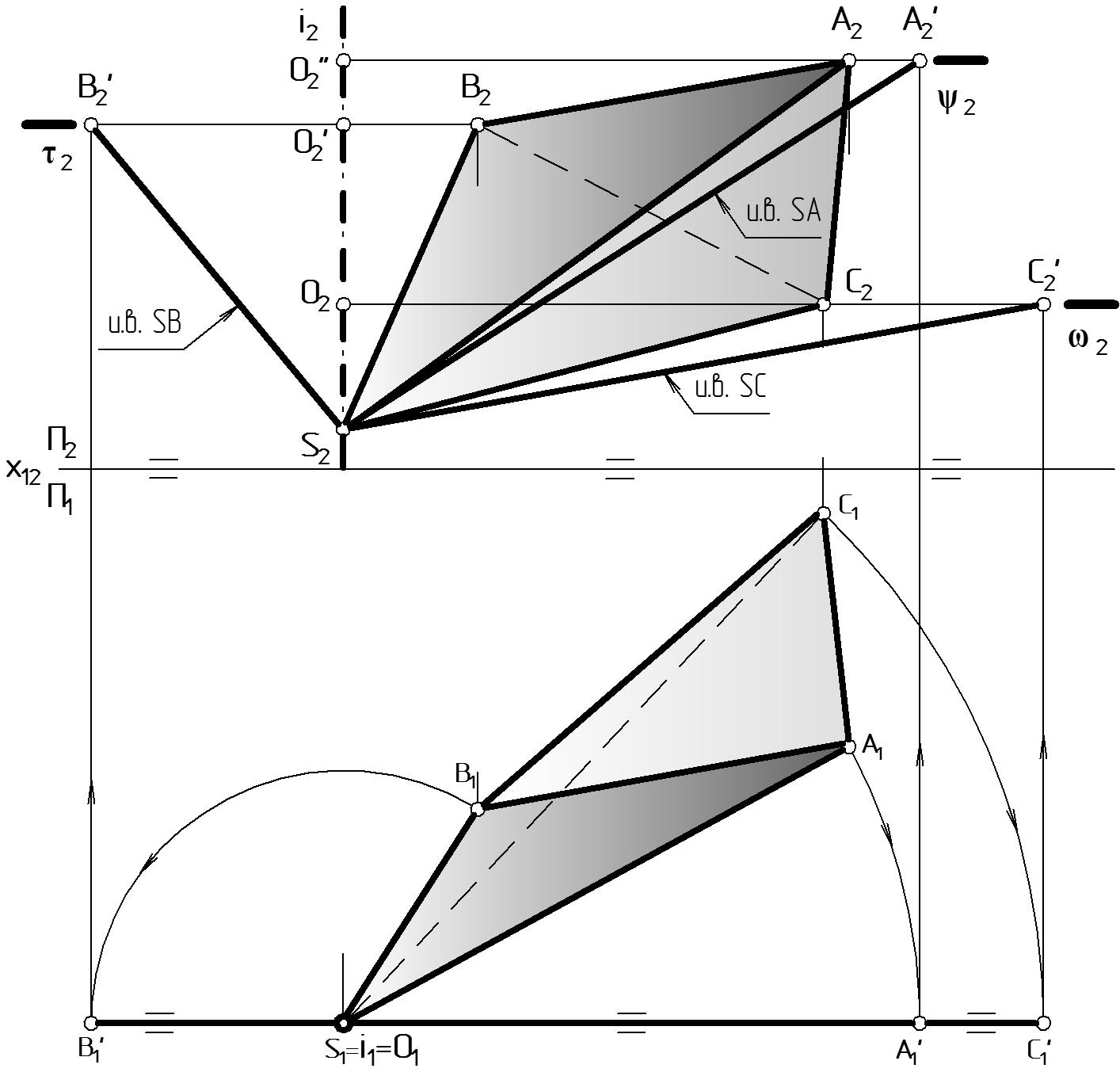
Этап 1. На Рис. 68 способом вращения найдены истинные величины боковых ребер SA, SВ, SС.

Рисунок 68

Чертеж выполняют в следующем порядке:

• выбирают положение оси вращения так, чтобы она проходила через вершину пирамиды, i  S, i  П₁. При этом точка S не меняет своего положения;

• горизонтальные проекции точек А₁, С₁ перемещаются вокруг оси вращения i₁ по дугам окружностей по часовой, а проекция В₁ – против часовой стрелки, до тех пор, пока вращающиеся отрезки не займут частное положение, параллельное плоскости П₂: А’₁S₁ // x₁₂, В’₁S₁ // x₁₂, С’₁S₁ // x₁₂;

• фронтальные проекции точек А₂, С₂ перемещаются вправо, а В₂ – влево, по окружностям, полностью совпадающим со следами соответствующих плоскостей вращения ₂, ₂, ₂, перпендикулярным оси вращения i₂;

• для нахождения точек А’₂, В’₂, С’₂ необходимо из А’₁, В’₁, С’₁ восставить линии связи, перпендикулярные x₁₂, и отметить точки пересечения со следами плоскостей ₂, ₂, ₂;

• соединив проекции А’₂, В’₂, С’₂ с неподвижной вершиной S₂, получим изображение ребер в истинную величину.

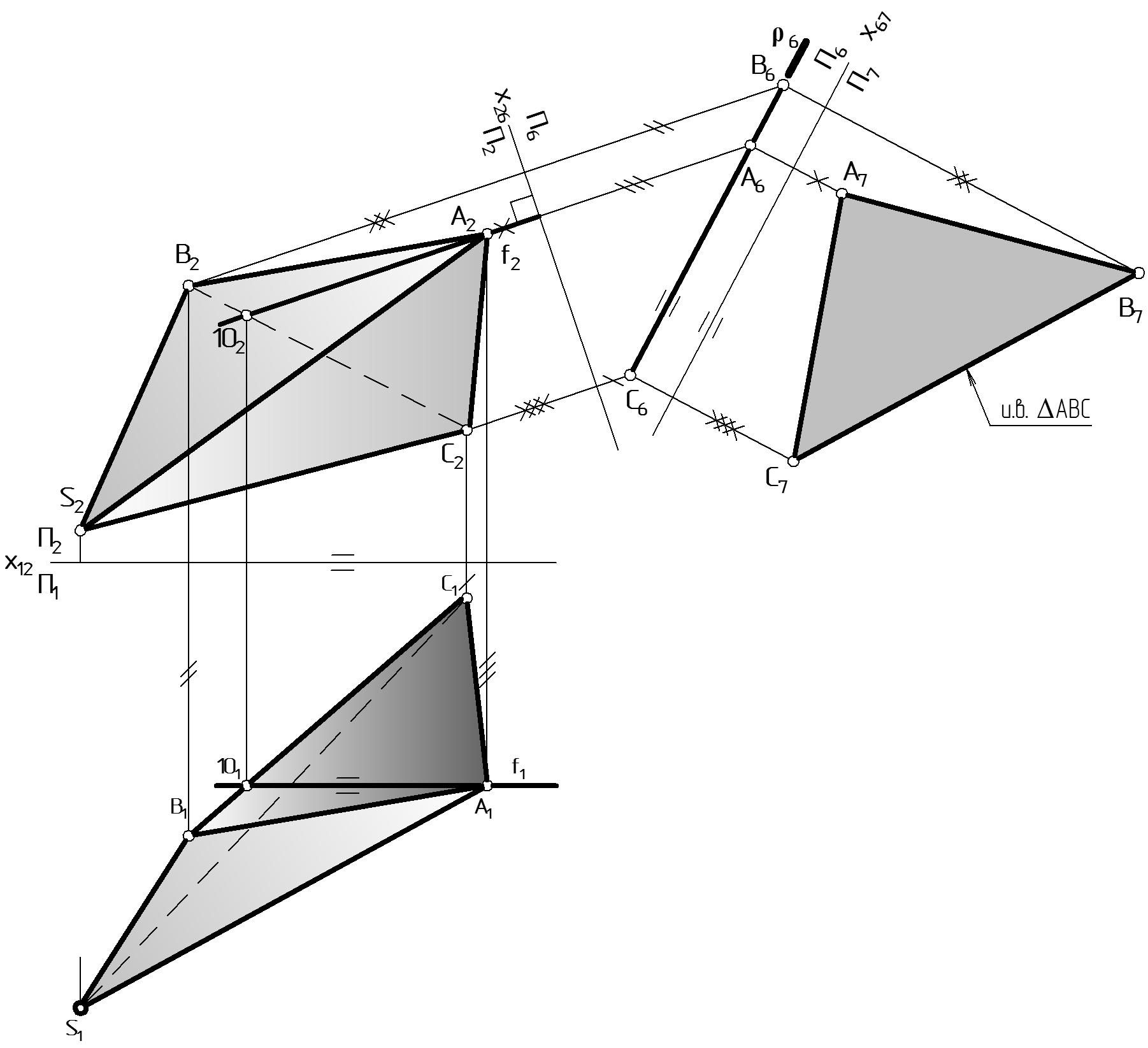
Этап 2. На Рис. 69 способом замены плоскостей проекций найдена истинная величина основания пирамиды  (AВС).

Рисунок 69

Первой переменой П₁  П₆ плоскость основания превращается в проецирующую плоскость:  (АВС) - о.п.   (АВС)  П₆:

• строят проекции фронтали плоскости f (f₁, f₂)   (АВС) (порядок построения фронтали плоскости показан на рис. 30 б).

Замечание: В качестве опорной прямой вместо фронтали f можно использовать горизонталь h плоскости, решение при этом будет соответствовать замене П₂  П_6.

• на плоскости П₂ выбирают положение оси х₂₆ на произвольном расстоянии перпендикулярно фронтальной проекции фронтали плоскости f₂: х₂₆  f₂;

• проводят линии связи от точек А₂, В₂, С₂ перпендикулярно новой оси х₂₆;

• откладывают от оси х₂₆ глубину точек y_A, y_B, y_C, взятые с плоскости П₁ (это отмечено штрихами); полученные проекции индексируют A₆, В₆, С₆;

• соединив проекции A₆, В₆, С₆, получим изображение плоскости ₆: проекция фигуры полностью совпадает с следом плоскости: (А₆В₆С₆)  ₆.

Второй переменой П₂  П₇ плоскость основания превращается в плоскость уровня  (АВС)  П₆   (АВС) // П₇. Плоскость П₁ и соответствующая проекция основания в этом этапе решения не участвует:

• на плоскости П₆ выбирают положение оси х₆₇ на произвольном расстоянии параллельно проекции плоскости ₆: х₆₇ // ₆;

• проводят линии связи от точек A₆, В₆, С₆ перпендикулярно новой оси х₆₇;

• откладывают от оси х₆₇ высоты точек z_A, z_B, z_C взятые с плоскости П₂ (это отмечено крестиками). Заметим, что z_A, z_B, z_C равны расстоянию от заменяемых проекций точек А₂, В₂, С₂ до предыдущей оси х₂₆, поскольку ось х₁₂ в этом этапе задачи не участвует; полученные проекции индексируют A₇, В₇, С₇;

• соединив проекции A₇, В₇, С₇, получим изображение основания в истинную величину: А₇В₇С₇ = и.в. АВС.

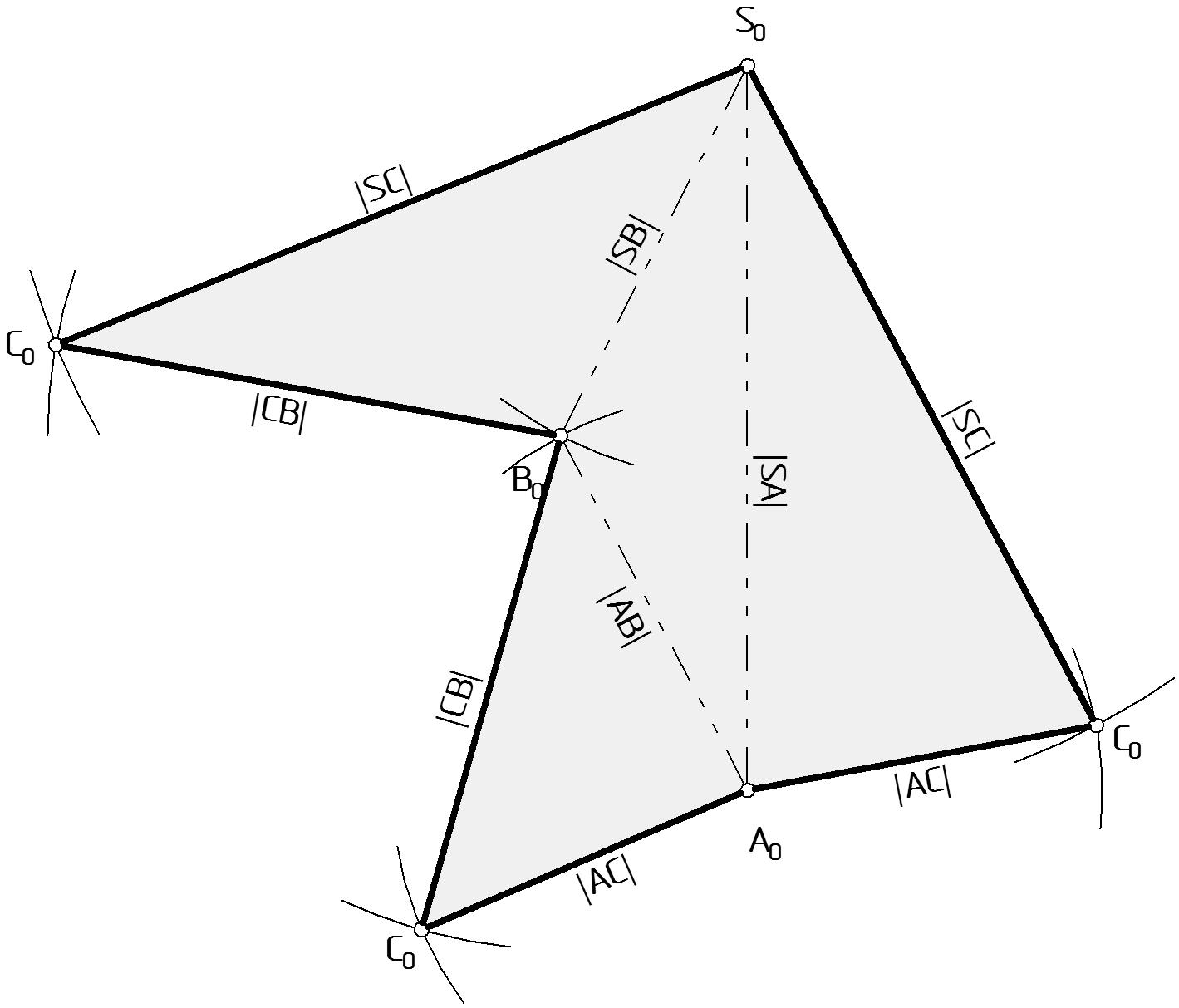
Этап 3. На Рис. 70 способом триангуляции построены грани пирамиды.

Построим грань S₀А₀В₀. Для этого через произвольную точку S₀ проводим прямую. Откладываем на ней от точки S₀ отрезок, равный SА, получим точку А₀. Из точки А₀ проводим дугу радиусом АB, взятым с истинной величины основания АВС. Из точки S₀ – дугу радиусом SВ. Пересечение дуг укажет положение вершины В_0.

Аналогично находятся точки С₀ . Получим грани S₀В₀С₀ и S₀С₀А_0.

Далее пристраивается истинная величина основания.

Контур развертки обводится основной линией, линии сгиба – тонкой штрих-пунктирной с двумя пунктирами.

Рисунок 70

Развертка призмы осуществляется методом нормального сечения:

1. преобразуют чертеж так, чтобы боковые ребра призмы проецировались в истинную величину;

2. пересекают призму вспомогательной плоскостью , перпендикулярной ее боковым ребрам (плоскость нормального сечения);

3. определяют истинную величину нормального сечения;

4. по найденному нормальному сечению и ребрам строят боковые грани, затем пристраивают основание.

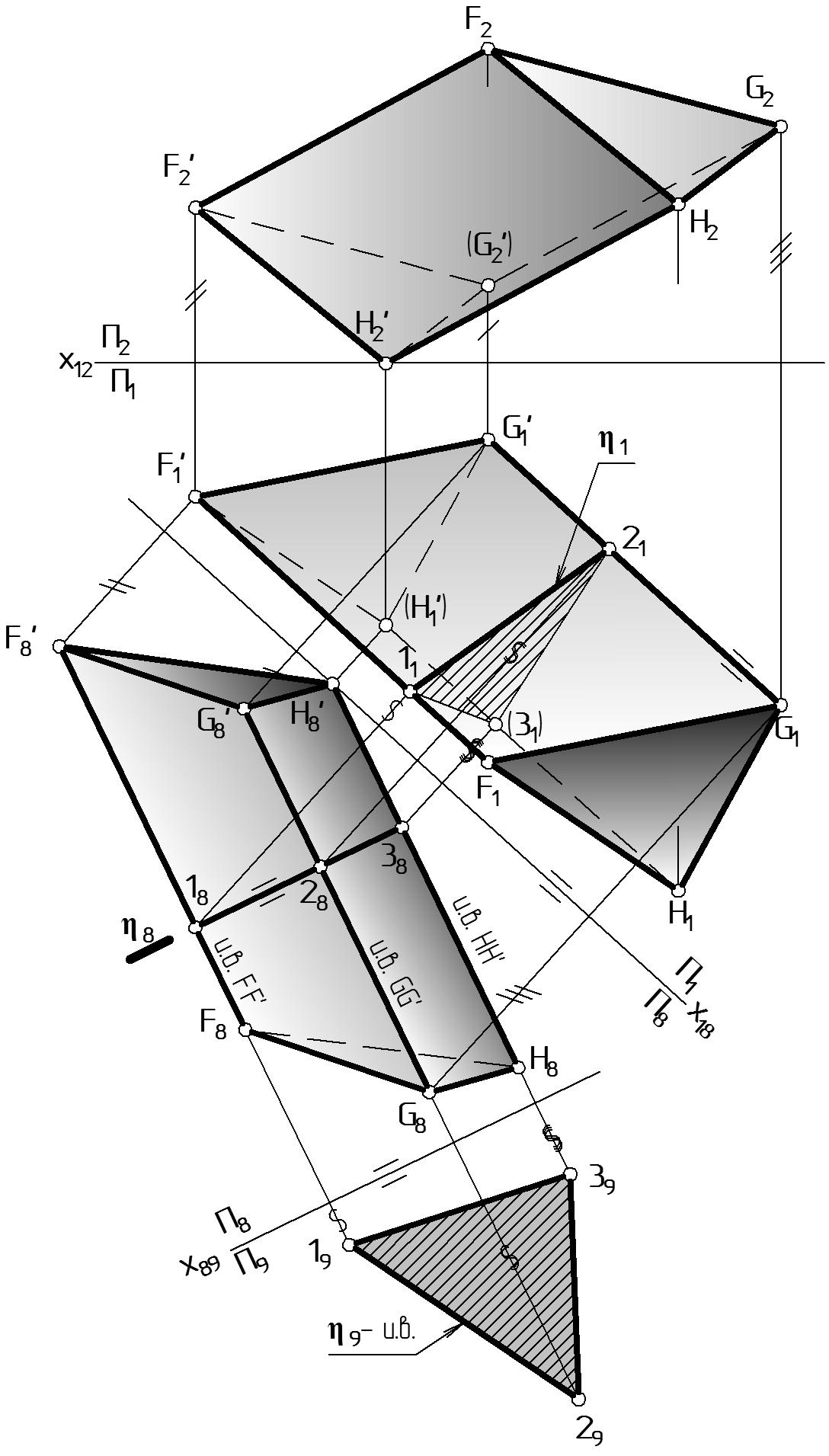
Этап 1. На Рис. 71 способом замены плоскости П₂  П₈ преобразуют чертеж так, чтобы боковые ребра призмы стали параллельны новой плоскости проекций П₈. Тогда на эту плоскость боковые ребра проецируются в натуральную величину. Решение выполняют в порядке:

• на П₁ выбирают положение оси х₁₈ параллельно горизонтальным проекциям ребер призмы: х₁₈ // G₁G₁’// H₁H₁’// F₁F₁’;

• проводят линии связи от вершин призмы F₁, G₁, H₁, G₁’, … перпендикулярно новой оси х₁₈;

• откладывают от оси х₁₈ высоты точек z_F, z_G, …, взятые с плоскости П₂ (отмечено штрихами), полученные проекции индексируют F₈, G₈, H₈, _…;

• соединив проекции, получим изображение призмы, боковые ребра которой равны истинной величине.

Рисунок 71

Этап 2. Построение фигуры нормального сечения:

• строят плоскость (₈), след которой перпендикулярен ребрам призмы; отмечают точки 1₈, 2₈, 3₈ пересечения следа ₈ с ребрами;

• полученные на плоскости П₈ точки пересечения ребер призмы со следом плоскости ₈ (1₈, 2₈, 3₈) обратным проецированием переносятся последовательно на исходные проекции тех же ребер на П₁ по линиям связи, перпендикулярным х₁₈;

• соединив построенные точки 1₁, 2₁, 3₁ прямыми, получим фигуру нормального сечения ₁(1₈2₈3₈).

Этап 3. Для нахождения истинной величины нормального сечения заменим плоскость П₁  П₉ так, чтобы плоскость сечения ₈ стала параллельна новой плоскости проекций П₉. С этой целью:

• на плоскости П₈ выбирают положение оси х₈₉ на произвольном расстоянии параллельно плоскости сечения ₈: х₈₉ // ₈;

• проводят линии связи от точек 1₈, 2₈, 3₈ перпендикулярно новой оси х₈₉;

• откладывают от оси х₈₉ глубины точек y₁, y₂, y₃, взятые с плоскости П₁ (отмечено волнами), полученные проекции точек индексируют 1₉, 2₉, 3₉;

• соединив точки 1₉, 2₉, 3₉, получим изображение нормального сечения в истинную величину ₉ – и.в.

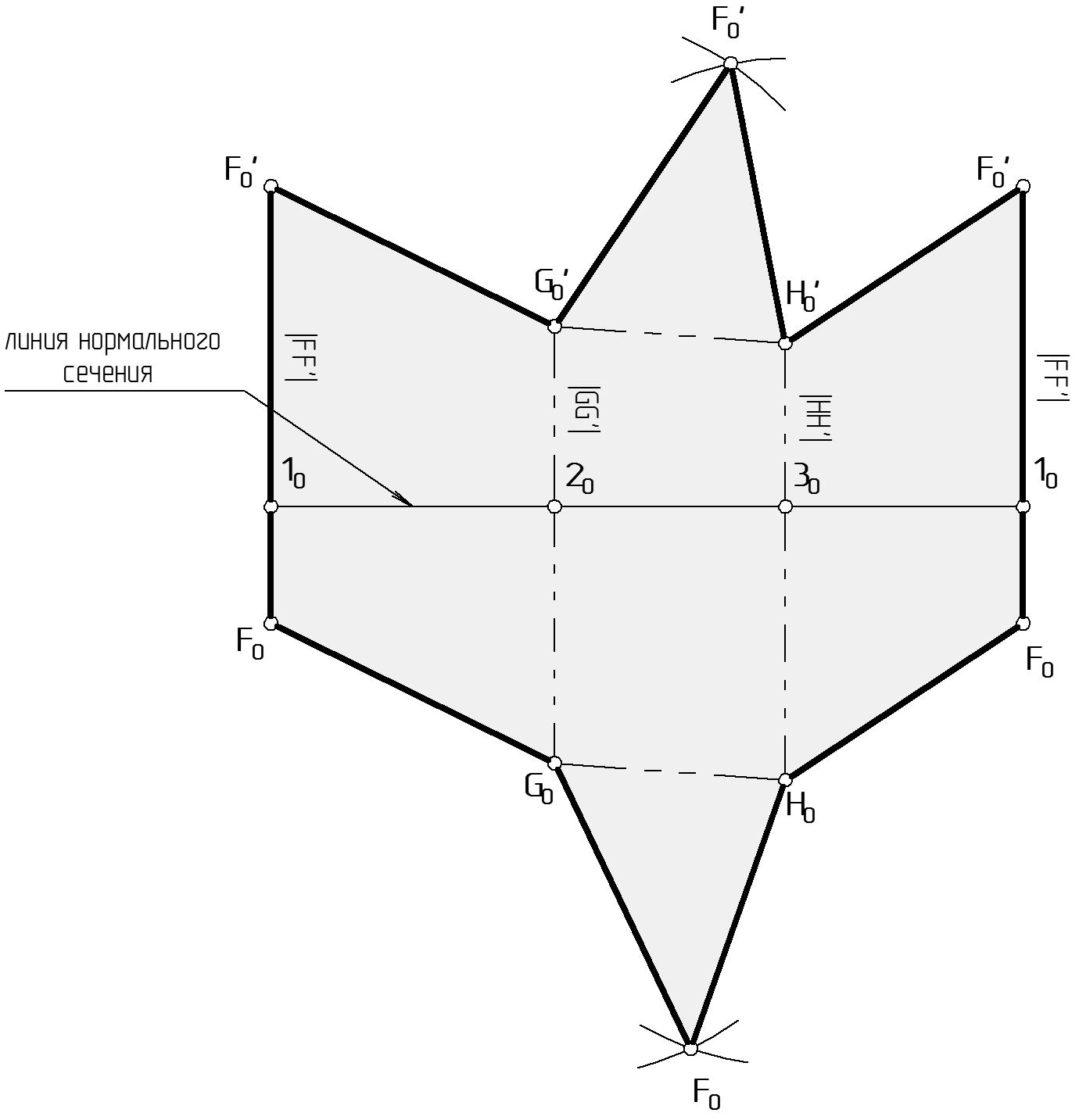
Этап 4. На Рис. 72 построена развертка призмы. Для этого:

• строим линию нормального сечения: на произвольной горизонтальной прямой откладываем отрезки, равные истинным величинам сторон нормального сечения ₉: 1₀2₀, 2₀3₀, 3₀1₀;

• через точки 1₀, 2₀, 3₀, 1₀ проведем прямые, перпендикулярные к линии нормального сечения и отложим на них отрезки, соответствующие истинной величине боковых ребер FF’=F₀F’₀, GG’=G₀G’₀, HH’=H₀H’₀ c соблюдением пропорционального деления ребер точками нормального сечения 1₀, 2₀, 3₀, 1₀;

• полученные концевые точки соединяем прямыми F₀G₀, G₀H₀, H₀F₀, F’₀G’₀, G₀’H₀’, H₀’F₀’. Полученная плоская фигура есть развертка боковой поверхности призмы;

• далее необходимо пристроить верхнее и нижнее основания призмы. В случае треугольной пирамиды пересечение дуг укажет положение вершин: F₀G₀  H₀F₀ = F₀, F’₀G’₀  H₀’F₀’ = F₀’_.

Контур развертки обводится основной линией, линии сгиба – тонкой штрих-пунктирной с двумя пунктирами.

Рисунок 72

Замечание: Если у призмы четырехугольное основание, то его необходимо предварительно разбить диагональю на два треугольника. Определить истинную величину диагонали основания любым способом. При компоновке развертки составить основание из двух треугольников.