4.Определение видимости сечения

Определение видимости сечения следует выполнять после определения собственной видимости ребер многогранника.

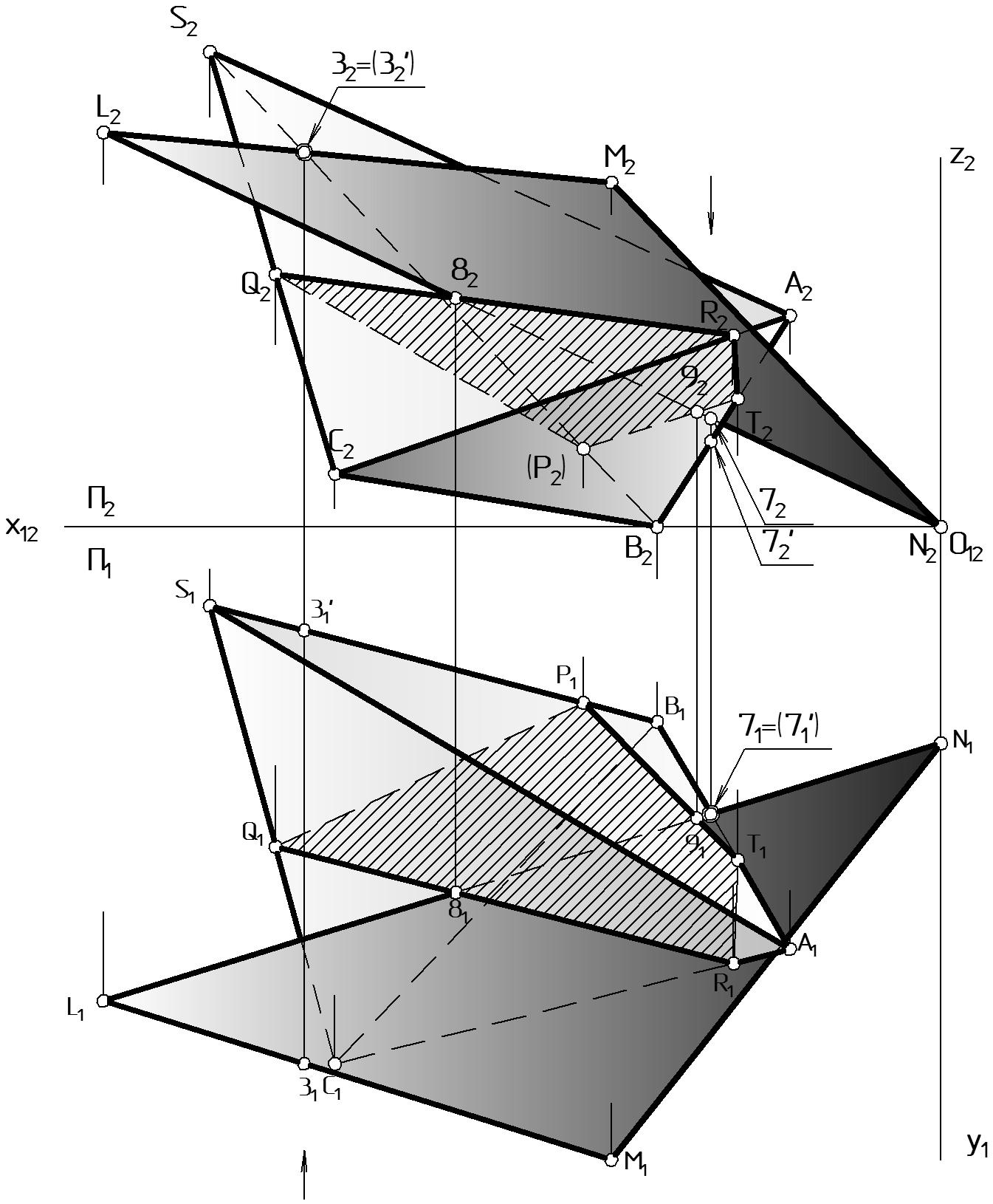
При соединении точек ломаной сечения следует руководствоваться видимостью соответствующих граней: в видимой грани лежит видимая часть ломаной, в невидимой грани – невидимая часть. Например (Рис. 62, Рис. 64), на П₂ видимыми являются проекция боковой грани S₂A₂C₂ и соответственно прямая R₂Q₂  S₂A₂C₂; проекция основания A₂B₂C₂ и соответственно прямая R₂T₂  A₂B₂C₂. Невидимыми являются проекции боковых граней S₂A₂В₂ и соответственно прямая T₂(P₂)  S₂A₂В₂; S₂B₂С₂ и соответственно прямая Q₂(P₂)  S₂B₂С₂.

Замечание: после определения видимости линии сечения, в случае необходимости, обозначения невидимых точек сечения заключают в скобки. Например, (Р₂).

5.Определение относительной видимости многогранника и секущей плоскости

Определение относительной видимости многогранника и плоскости  необходимо вести с учетом непрозрачности.

В зонах не наложения отсека плоскости и пирамиды обе фигуры видимы.

Видимость в границах наложения проекций пирамиды и плоскости определяется из чертежа исходя из следующих закономерностей:

• часть прямой, принадлежащей плоскости, заключенная между точками пересечения с контуром сечения, находится внутри многогранника и, следовательно, не видна;

• прямая, не пересекающаяся с контуром сечения, находится вне многогранника, ее видимость определяется методом конкурирующих точек.

Например (Рис. 65), часть прямой [LN] пересекает контур сечения в точках 8 и 9. Участок [89] прямой [LN] находится внутри многогранника и, следовательно, не виден П₁ и П₂. Видимость оставшихся прямых плоскости  на П₂ определена при помощи пары конкурирующих точек 3 и 3’(3₂ = 3’₂), одна из которых принадлежит прямой [L₂M₂] плоскости , а другая ребру пирамиды. Горизонтальная проекция точки 3 (3₁) имеет большую координату y, чем проекция точки 3’ (3’₁), следовательно, прямая [L₂M₂] видима, в этой зоне плоскость закрывает пирамиду.

Рисунок 65

Для определения видимости на П₁ взята пара конкурирующих точек 7 и 7’(7₁ = 7’₁) одна из которых принадлежит прямой [LN] плоскости , а другая ребру пирамиды [AB]. Так как фронтальная проекция точки 7 (7₂) имеет большую координату z чем фронтальная проекция точки 7’ (7’₂), то прямая [L₁N₁], которой принадлежит точка 7 на П₁ в границах наложения до точки 9₁, видима.

Замечание: в случае необходимости после определения относительной видимости обозначения невидимых точек заключают в скобки, невидимые части прямых оформляют штриховой линией.

6.Определение истинной величины сечения

Определение истинной величины сечения выполняют с использованием преобразования чертежа. Плоскость сечения следует последовательно преобразовывать в проецирующую, т.е. перпендикулярную одной из плоскостей проекций, а затем в плоскость уровня, т.е. параллельную одной из плоскостей проекций.

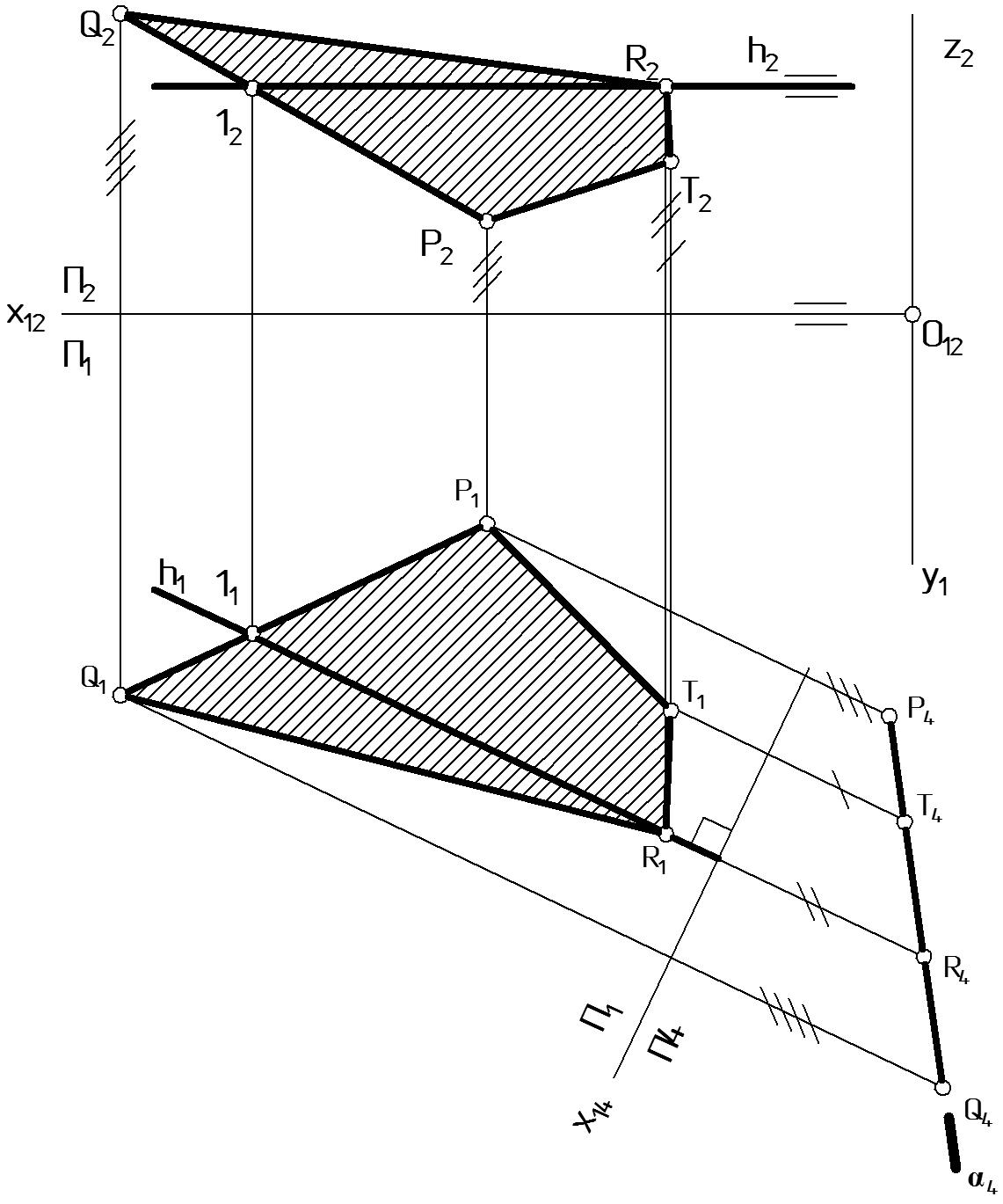
Преобразуем  (PTRQ) – о.п.   (PTRQ)  П₄. Для этого заменим П₂ на П₄, перпендикулярную П₁ и горизонтали h данной плоскости (Рис. 66). Положение П₄ однозначно определится осью х₁₄  h₁.

Рисунок 66

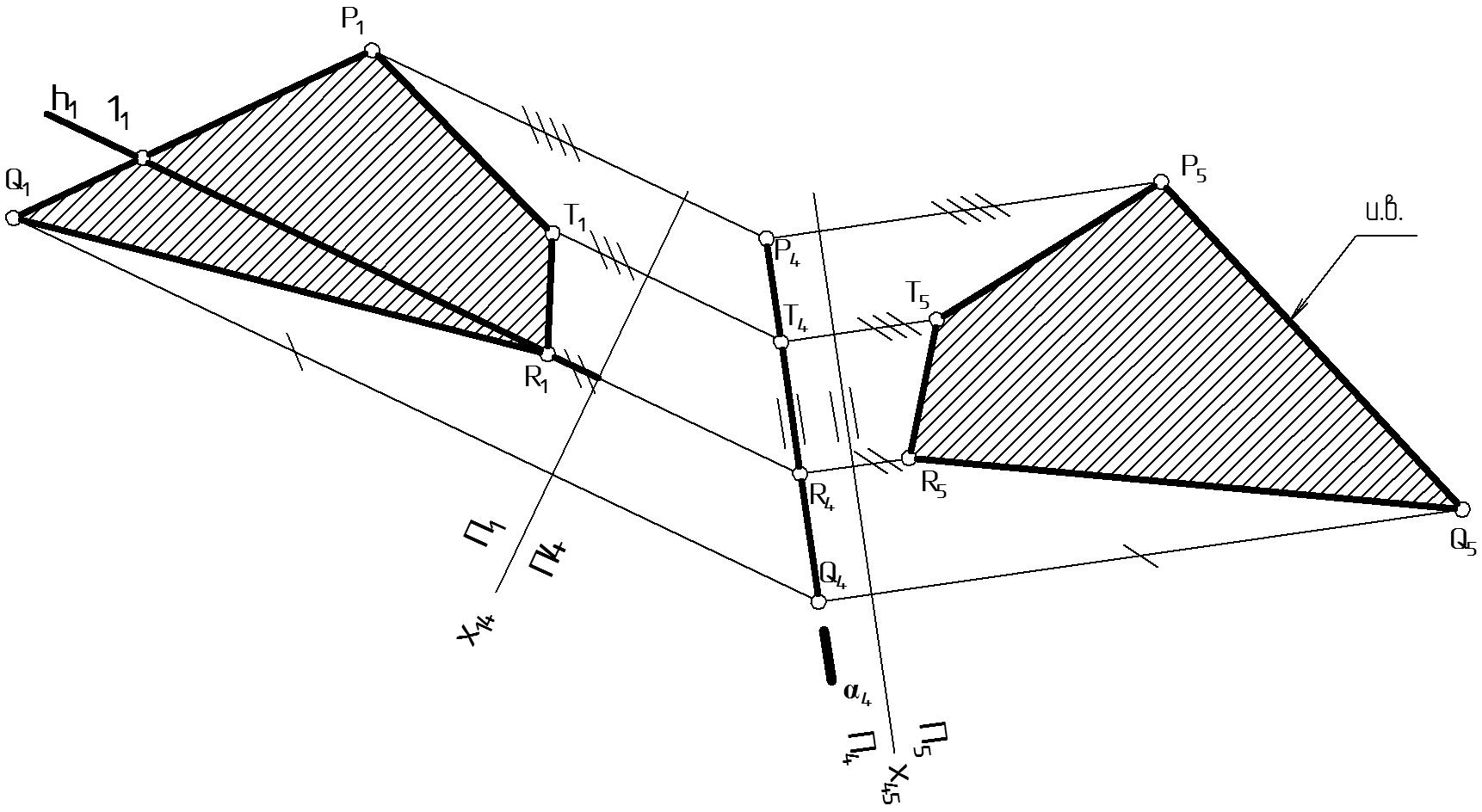
Построения выполняются аналогично построениям, показанным на Рис. 63. В результате преобразования на П₄ проекция сечения полностью совпадает со следом плоскости: (P₄, T₄, R₄, Q₄)  ₄.Преобразуем  (PTRQ)  П₄   (PTRQ)  П₅. Для этого заменим П₁ на П₅, перпендикулярную П₄ и параллельную следу ₄ (Рис. 67). Положение П₅ однозначно определится осью х₄₅ // ₄.

Рисунок 67

Построения выполняются аналогично построениям, показанным на Рис. 42. В результате преобразования проекция линии сечения на П5 равна истинной величине: P5T5R5Q5 = и.в. PTRQ.