3. Построение линии пересечения многогранника заданной плоскостью общего положения

В результате сечения поверхности плоскостью образуется линия, одновременно принадлежащая и поверхности, и плоскости. Такая линия называется линией пересечения поверхности плоскостью.

Замкнутая фигура, образованная линией пересечения поверхности тела секущей плоскостью, называется сечением и является частью секущей плоскости, заключенной внутри поверхности.

В общем случае линия пересечения многогранной поверхности с плоскостью представляет собой ломаную, т.е. линию, состоящую из прямолинейных отрезков, каждый из которых является линией пересечения соответствующей грани многогранника (грань - часть плоскости) с секущей плоскостью. Напомним, что линия пересечения двух плоскостей - прямая.

Точки перелома ломаной являются точками пересечения ребер многогранной поверхности с секущей плоскостью. Следовательно, линию пересечения можно построить по точкам пересечения ребер многогранника с секущей плоскостью (задача на построение точки пересечения прямой с плоскостью общего положения - первая позиционная задача);

Решение задачи возможно двумя способами: с применением алгоритма первой позиционной задачи, с применением метода преобразования чертежа.

Способ 1. Пусть в пространстве заданы плоскость  - секущая плоскость и прямая a – одно из ребер многогранника. Для решения вопроса об относительном положении прямой и плоскости через прямую а проводится посредник - вспомогательная секущая плоскость , строится линия пересечения b данной плоскости  с плоскостью . При этом возможны следующие случаи относительного положения прямых а и b, лежащих в плоскости :

1. Прямая b совпадает с прямой а. Т. к. прямая b, как линия пересечения плоскостей  и , лежит в плоскости , то в этом случае прямая а лежит в плоскости . Пересечения нет. Прямая а полностью видима.

2. Прямая b параллельна а. В этом случае прямая а параллельна плоскости . На чертеже прямая a или полностью видима, или полностью не видима по отношению к отсеку непрозрачной плоскости.

3. Прямая b пересекает а. В этом случае прямая а пересекает плоскость . Точка К пересечения а с b принадлежит одновременно обеим прямым. Но т.к. прямая b лежит в плоскости  , то все ее точки, в том числе точка К, принадлежат этой плоскости. Следовательно, точка К является единственной общей точкой для данных прямой а и плоскости . Но такой точкой может быть только точка пересечения прямой с плоскостью. Часть прямой видима по отношению к непрозрачной плоскости, часть - нет. Пересечение имеет место.

Поясним сказанное на примере.

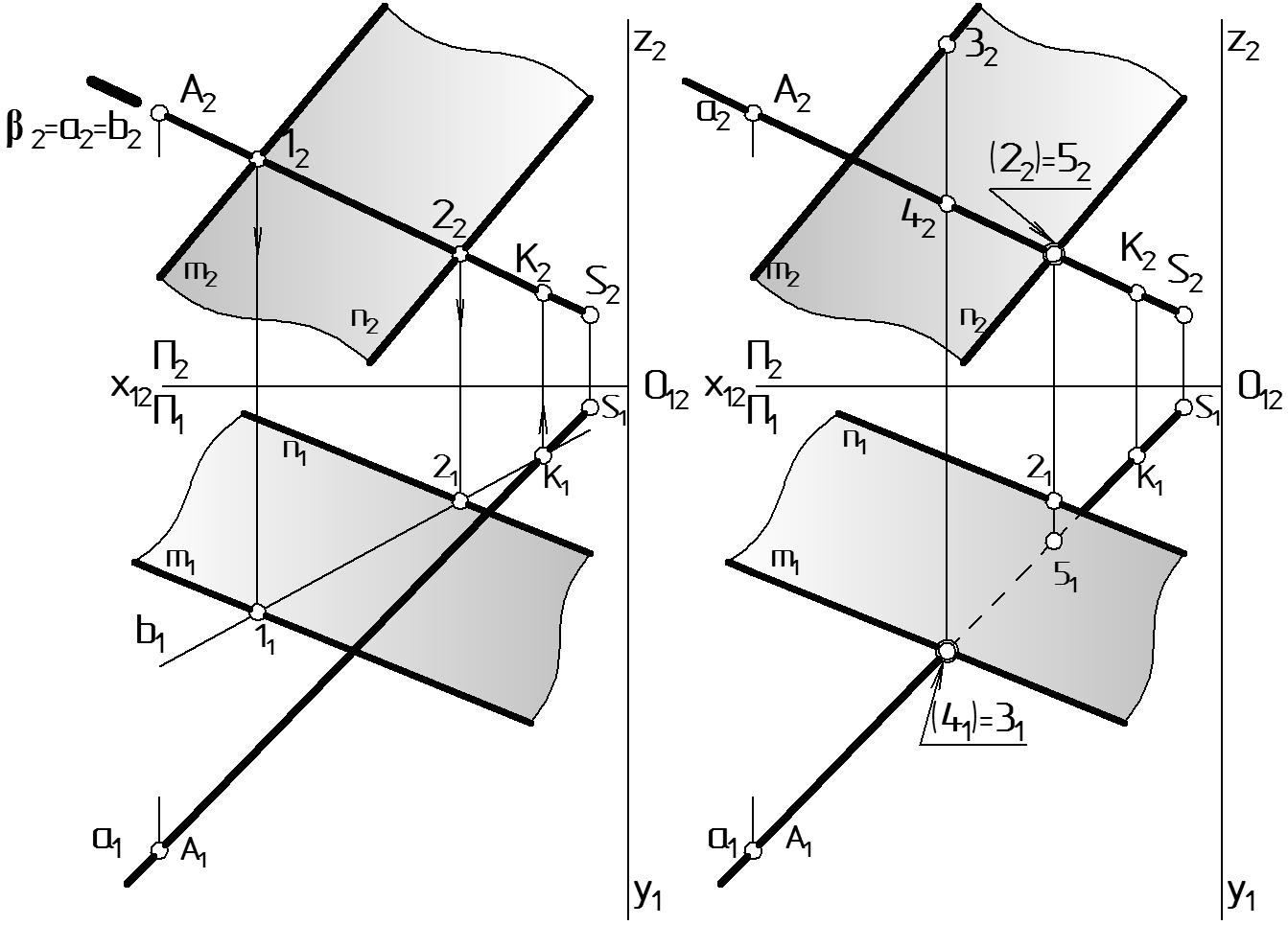
На комплексном чертеже построим точку К пересечения прямой а (А, S), заданной точками A, S, с плоскостью  (m  n), заданной параллельными прямыми m и n, определим видимость прямой а относительно отсека плоскости (Рис. 58).

Дано: а (А, S) – о.п.,  (m  n) – о.п. Найти: К = а  , определить видимость а.

а б Рисунок 58

Решение. Алгоритм нахождения точки К включает три этапа, результат которого показан на Рис. 58 a.

Этап 1. Прямую а (А, S) общего положения заключают во вспомогательную проецирующую плоскость-посредник. В данном случае это фронтально-проецирующая плоскость ( ₂ )  П₂, которая на чертеже задается фронтальным следом ₂ с указанием собирательного свойства следа отрезком утолщенной линии. След совпадает с проекцией прямой а₂, что отображается равенством ₂ = а₂. Проекция прямой а₁ в этом этапе не участвует.

Этап 2. Находится линия пересечения b вспомогательной проецирующей плоскости-посредника  с заданной плоскостью : b(12) =   . Проекции прямой a в этом этапе не участвуют.

Ход решения этого этапа соответствует решению Задачи 3, показанной на рис. 32. Фронтальная проекция b₂ совпадает со следом плоскости-посредника (₂ = b₂) и пересекает прямые m₂, n₂ в точках 1₂ , 2₂: 1₂ = ₂  m₂; 2₂ = ₂  n₂. Горизонтальные проекции этих точек строятся по линии связи: 1₁  m₁; 2₁  n₁. Отрезок 1₁2₁ прямой b₁, одновременно принадлежит обеим плоскостям и, следовательно, является линией их пересечения.

Этап 3. Находится точка К пересечения заданной прямой а c найденной на втором этапе прямой b. Сначала точка отмечается на плоскости П₁: К₁ = а₁  b₁, затем по линии связи находится К₂  а₂.

В результате этих трех этапов найдена точка К (К₁; К₂) пересечения прямой общего положения а с плоскостью общего положения . Очевидно, что в найденной точке К (К₁; К₂) пересечения прямой с плоскостью меняется видимость прямой.

Видимость определяется по методу конкурирующих точек в два этапа, результаты которых показаны на Рис. 58 б.

Этап 4. Определяется видимость прямой а₁ относительно ₁ на горизонтальной плоскости проекций П₁. На П₁ возьмем пару конкурирующих точек 3, 4 , принадлежащих скрещивающимся прямой а₁ и прямой m1, принадлежащей _1. Пусть 3  m и 4  a. На П₁ проекции этих точек 3₁ и 4₁ совпадают. Вопрос видимости для 3₁ и 4₁ решается на П₂, где их проекции разнесены. На П₂ проекция точки 3₂ расположена выше проекции 4₂ (координата z₃ > z₄), следовательно, точка 3 расположена в пространстве выше точки 4 и прикрывает ее собой. Таким образом, на плоскости П₁ видна проекция точки 3₁ и прямая m1, к которой она относится, следовательно видна ₁. Невидимая на П₁ проекция 4₁ принадлежит прямой а₁, следовательно прямая невидима и обозначается штриховой линией.

Этап 5. Теперь определим видимость проекции а₂ относительно ₂ на П₂ Для этого в качестве конкурирующих выберем точку 2, принадлежащую прямой n, а значит плоскости , и точку 5, принадлежащую прямой a. Вопрос видимости для 2₂ и 5₂ решается на П₁, где их проекции разнесены. Посмотрим на П₁ глубина какой точки больше? Для этого сравним координаты y точек 2₁ и 5₁. y₅  y₂, то есть глубина точки 5 больше, следовательно, 5₂ видима. Отметим скобками, что проекция 2₂, которая принадлежит прямой n₂, невидима. Значит, прямая a₂ в этом месте находится перед плоскостью, она будет видима.

Используем приведенный алгоритм для решения задачи СГР.

Построим линию пересечения поверхности многогранника Ф (ABCS) с плоскостью, ограниченной отсеком  (LMN). Определим видимость на плоскостях проекций. Для этого решим последовательно задачи пресечения каждого ребра с плоскостью.

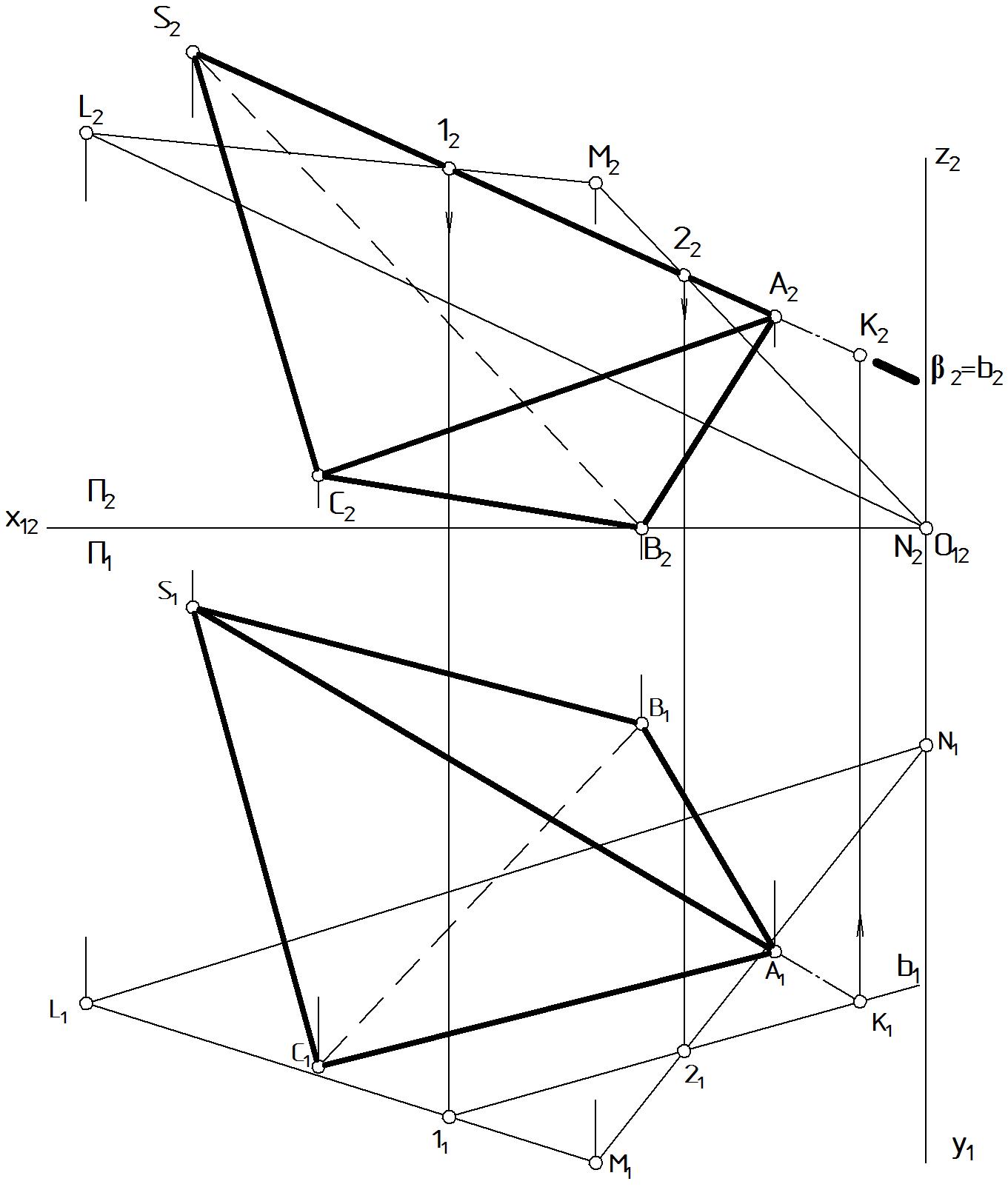
На комплексном чертеже (Рис. 59) показаны вспомогательные построения, в результате которых определяется точка пересечения ребрa пирамиды [SA] с плоскостью  (LMN).

Этап 1.1. Ребро многогранника [SA] заключают во вспомогательную проецирующую плоскость-посредник ( ₂ )  П₂, которая на чертеже задается фронтальным следом ₂. След совпадает с проекцией ребра ₂ = [S₂A₂].

Рисунок 59

Этап 1.2. Находится линия пересечения b вспомогательной плоскости-посредника  с заданной плоскостью : b(12) =   . Проекции ребра в этом этапе не участвуют. Фронтальная проекция b₂ совпадает со следом плоскости-посредника ₂ = b₂ и пересекает стороны треугольника LMN в точках 1₂ , 2₂: 1₂ = ₂  [L₂M₂]; 2₂ = ₂  [M₂N₂]. Горизонтальные проекции этих точек строятся по линии связи: 1₁  [L₁M₁]; 2₁  [M₁N₁]. Отрезок 1₁2₁ прямой b₁, одновременно принадлежит обеим плоскостям и, следовательно, является линией их пересечения.

Этап 1.3. Находится точка К пересечения ребра [SA] с найденной на втором этапе прямой b. Сначала точка отмечается на плоскости П₁: К₁ = [S₁A₁]  b₁ (в данном случае для получения точки пришлось продлить ребро), затем по линии связи находится К₂  [S₂A₂] (так же на продолжении ребра).

В результате этих трех этапов найдена точка К (К₁; К₂) пересечения ребра с плоскостью общего положения . К (К₁; К₂) =[SA] (LMN).

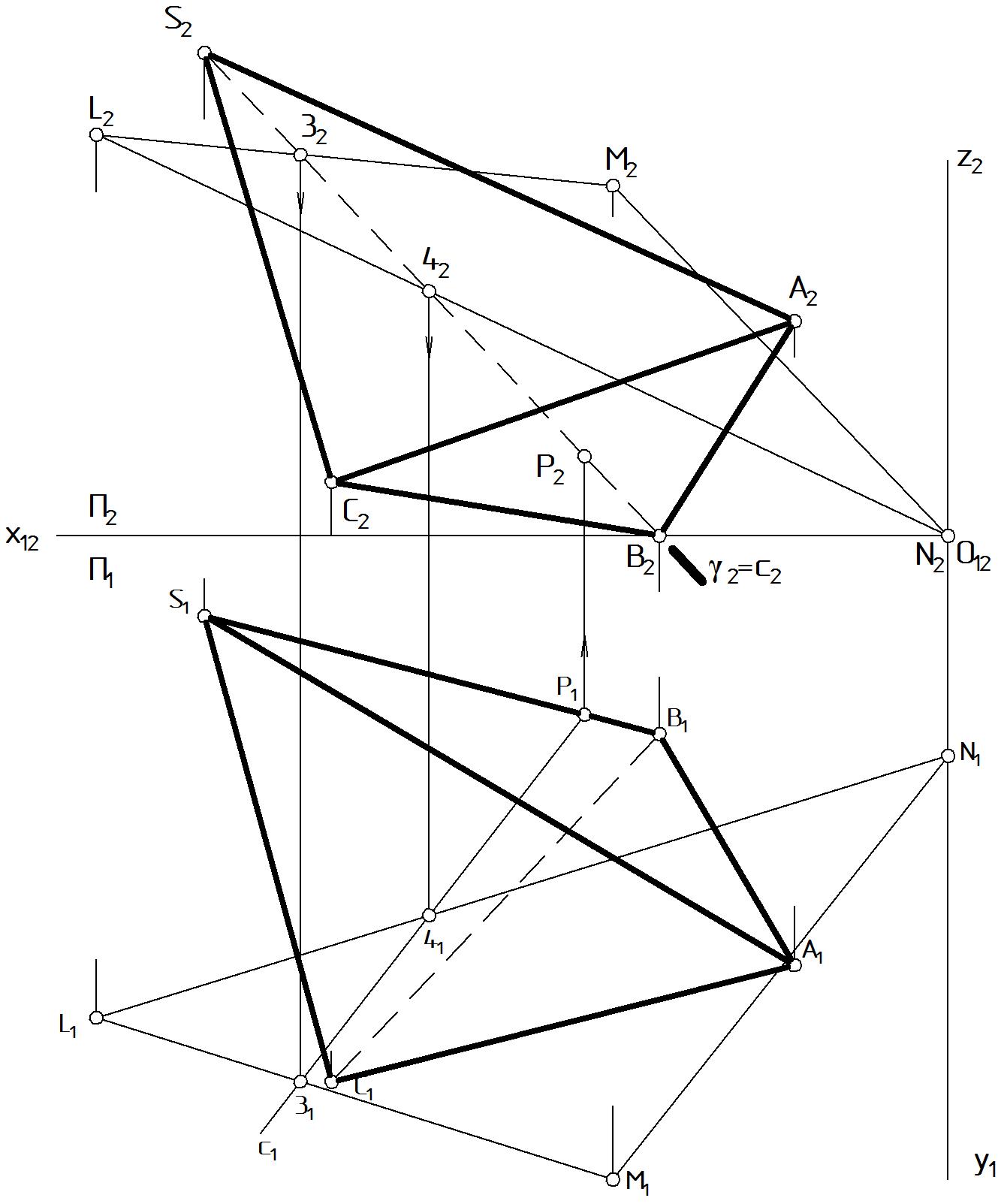
На комплексном чертеже (Рис. 60) показаны вспомогательные построения, в результате которых определяется точка пересечения ребрa [SB] пирамиды с плоскостью  (LMN).

Рисунок 60

Этап 2.1. ( ₂ )  П₂, которая на чертеже задается фронтальным следом ₂. След совпадает с проекцией ребра ₂ = [S₂B₂].

Этап 2.2. c(34) =   ; ₂ = с₂: 3₂ = ₂  [L₂M₂]; 4₂ = ₂  [L₂N₂]. 3₁  [L₁M₁]; 4₁  [L₁N₁].

Этап 2.3. P₁ = [S₁B₁]  c₁, P₂  [S₂B₂]  P (P₁; P₂) = [SB]  (LMN).

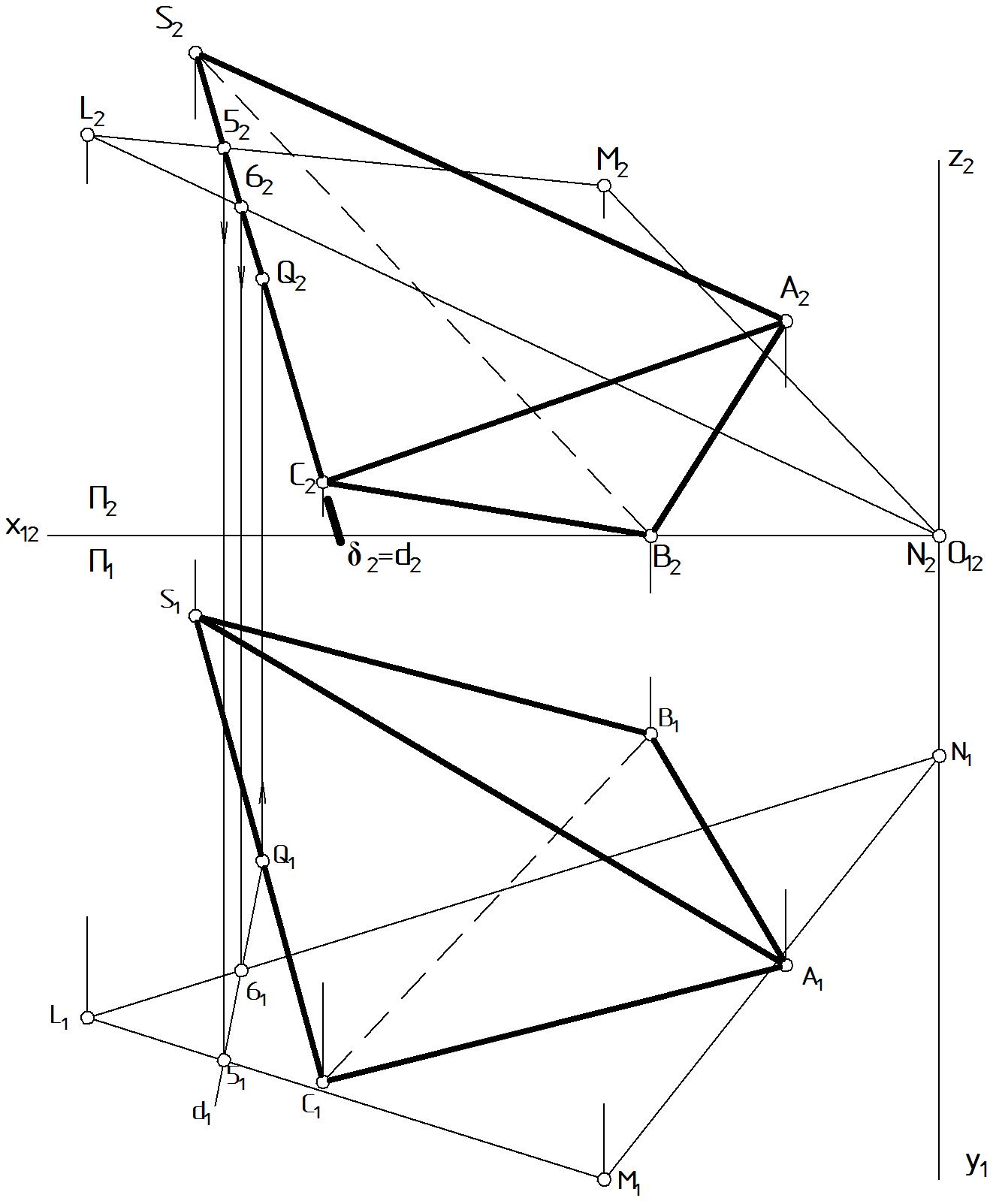
На комплексном чертеже (Рис. 61) показано определение точки пересечения ребрa [SC] пирамиды с плоскостью  (LMN).

Рисунок 61

Этап 3.1. ( ₂ )  П₂, ₂ = [S₂C₂].

Этап 3.2. d(56) =   ; ₂ = d₂: 5₂ = ₂  [L₂M₂]; 6₂ = ₂  [L₂N₂]. 5₁  [L₁M₁]; 6₁  [L₁N₁].

Этап 3.3. Q₁ = [S₁C₁]  d₁, Q₂  [S₂C₂]  Q (Q₁; Q₂) = [SC]  (LMN).

Замечание: если пирамида четырехугольная, необходимо повторить эти три этапа еще раз. Если боковые ребра не пересекают плоскости, следует рассмотреть ребра, входящие в основание многогранника.

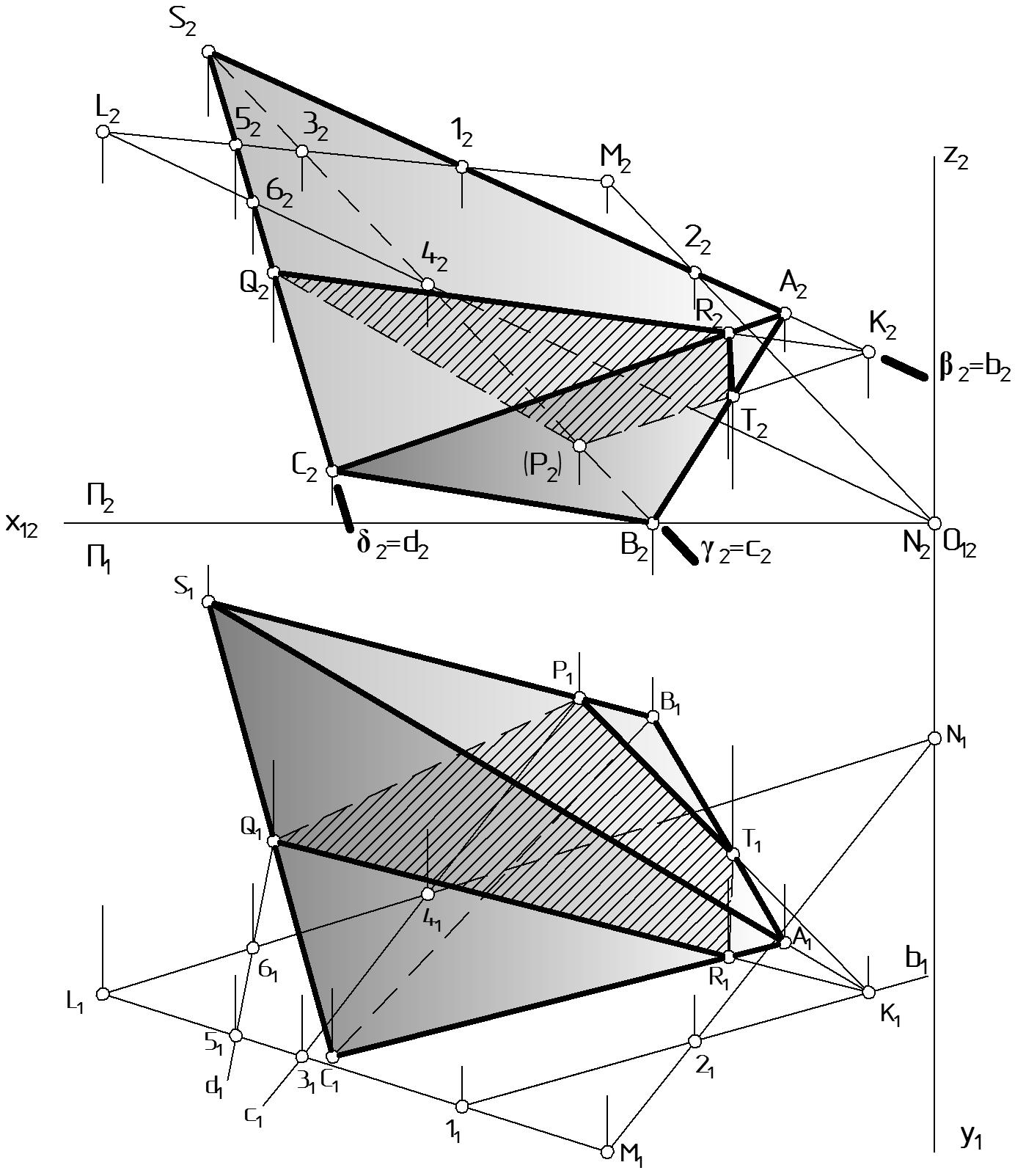
Соединив построенные точки K, P, Q прямыми, получим ломаную линию сечения боковой поверхности многогранника (Рис. 62).

Рисунок 62

Однако боковая поверхность многогранника не бесконечна, а ограничена плоскостью основания АВС, поэтому из полученной линии сечения KPQ поверхности пирамиды принадлежит часть, ограниченная ломаной QRTP (заштрихована), где точки R и T принадлежат плоскости основания АВС (Рис. 62).

Рассмотрим получение точек R и T. Соединив точки сечения K и P прямой, получим линию, принадлежащую плоскости SAВ. При пересечении прямой (KP) с ребром [AВ], получим точку T. Отрезок [RТ] принадлежит грани SAВ пирамиды. Аналогично (KQ)  [CA] = R; [RQ] принадлежит грани SAC. Отрезок [RT] принадлежит основанию ABC.

Способ 2. Применение метода преобразования комплексного чертежа к построению линии пересечения поверхности с плоскостью.

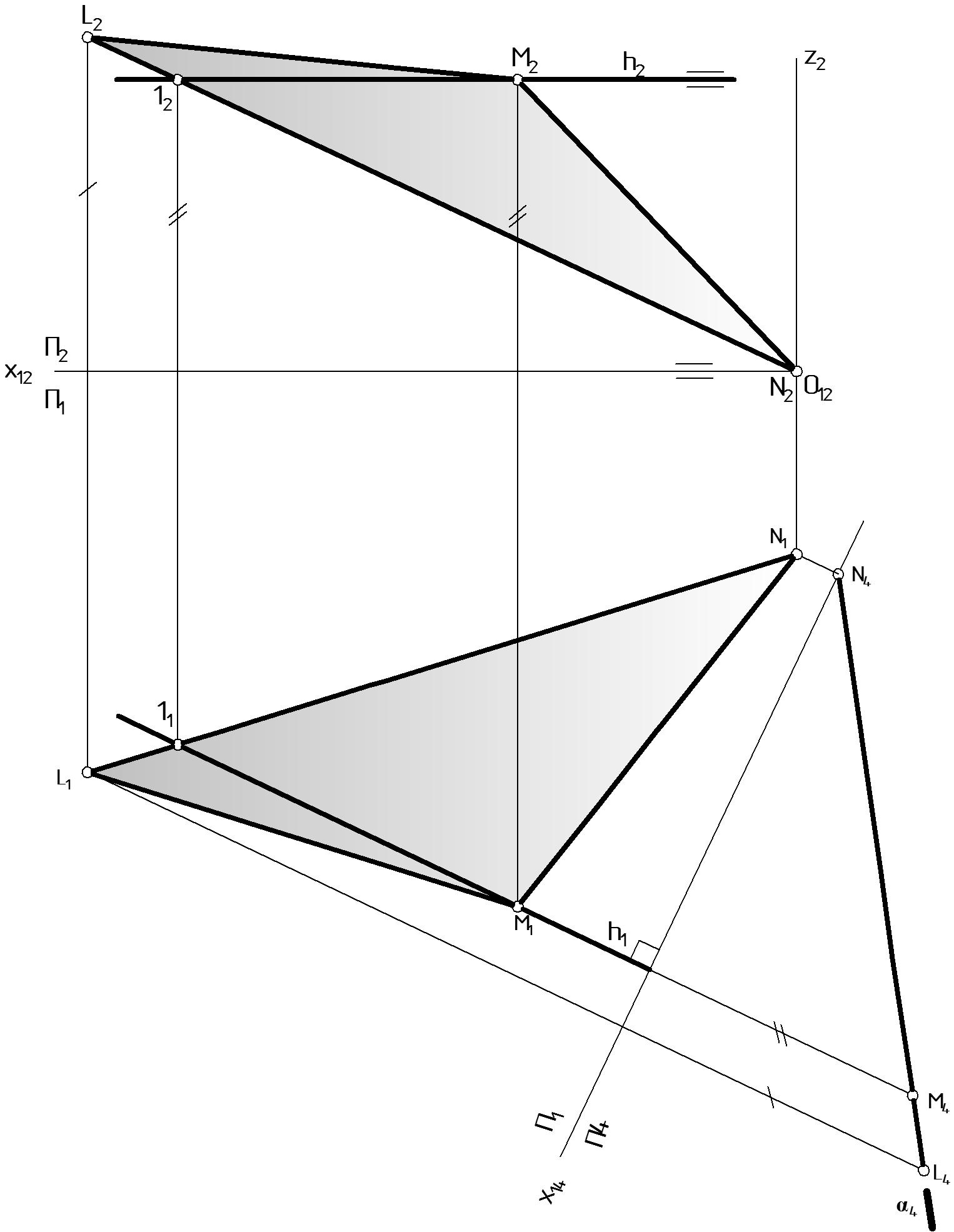
Исходные проекции данных поверхности и секущей плоскости  преобразуются так, чтобы  приняла частное положение, т.е. выполняется преобразование плоскости общего положения в проецирующую, например,  (LMN) – о.п.   (LMN) П₄ (Рис. 63).

Заменим П₂, на П₄, перпендикулярную П₁ и опорной прямой – горизонтали h данной плоскости . Положение плоскости П₄ однозначно определится осью х₁₄ = П₁  П₄ (см. Рис. 14).

Замечание: В качестве опорной прямой вместо горизонтали можно использовать фронталь f плоскости, решение при этом будет соответствовать замене П₁  П₄.

Порядок получения нового изображения плоскости следующий:

• строят проекции горизонтали плоскости h(h₁; h₂)   (порядок построения горизонтали плоскости показан на рис. 27, рис. 30 а);

• на плоскости П₁ выбирают положение оси х₁₄ перпендикулярно горизонтальной проекции горизонтали плоскости h₁: х₁₄  h₁;

• проводят линии связи от точек L₁, M₁, N₁, перпендикулярно новой оси х₁₄;

• откладывают от оси х₁₄ высоты точек z_L, z_M, z_N, взятые с плоскости П₂ (отмечено штрихами), высота точки N z_N=0, поэтому N₄ лежит на оси;

• полученные проекции индексируют L₄, M₄, N₄;

• соединив проекции L₄, M₄, N₄, получают изображение плоскости ₄. В соответствии с инвариантным свойством проецирования 6) если фигура перпендикулярна плоскости проекций П₄, то проекция фигуры полностью совпадает со следом плоскости: (L₄, M₄, N₄)  ₄.

Рисунок 63

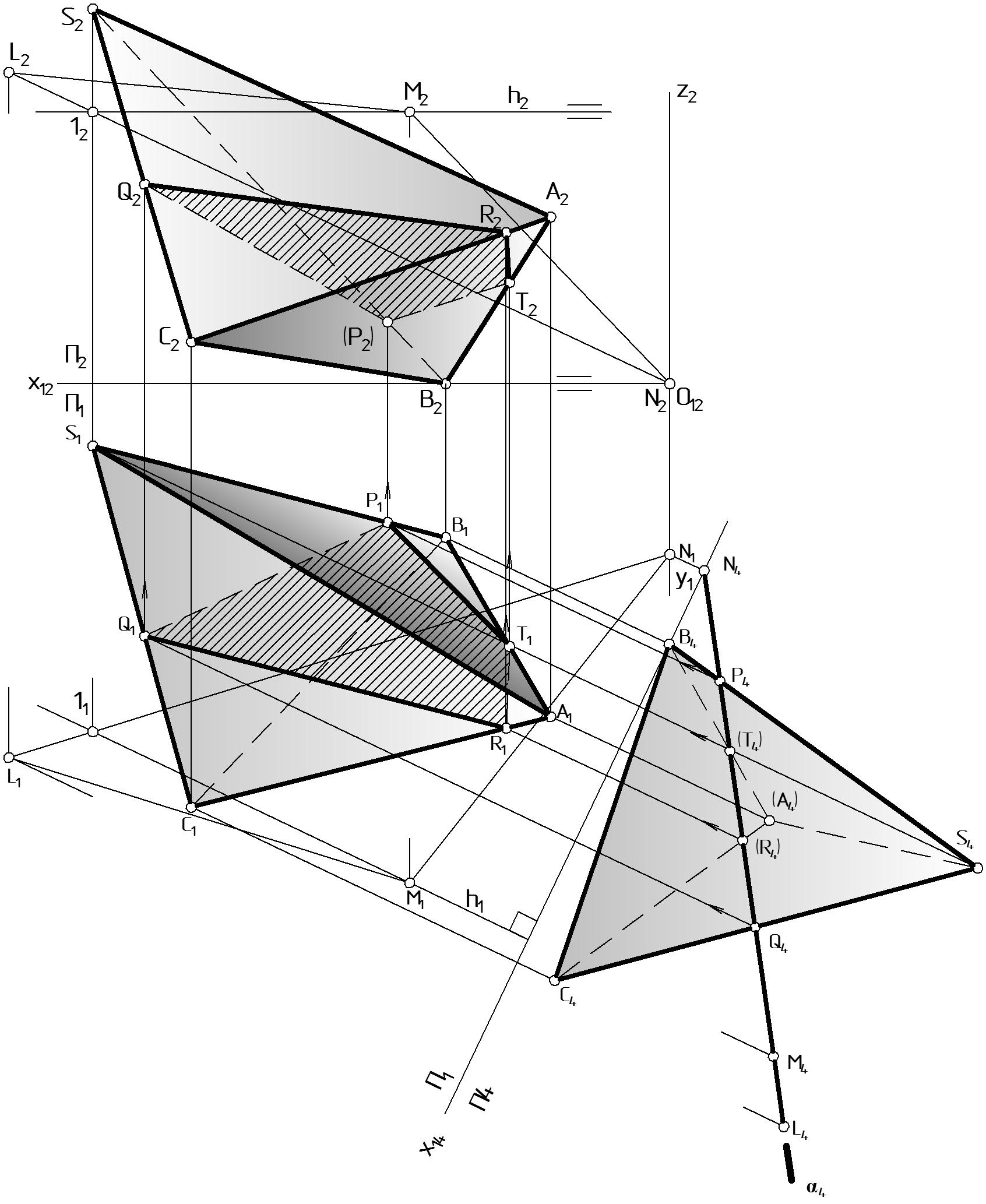
Аналогично построим новые проекции вершин многогранника S₄, А₄, В₄, C₄. Соединив их, получим проекцию многогранника на плоскости П₄ (Рис. 64).

Рисунок 64

Для определения видимости ребер многогранника на плоскости П₄ используется метод конкурирующих точек в системе плоскостей П₄/П₁ аналогично системе П₂/П₁ .

Полученные на плоскости П₄ точки пересечения ребер пирамиды со следом плоскости ₄ (P₄ = S₄B₄  ₄; T₄ = А₄B₄  ₄; R₄ = А₄B₄  ₄; Q₄ = S₄C₄  ₄) обратным проецированием переносятся последовательно на исходные проекции тех же ребер: на П₁ по линиям связи, перпендикулярным х₁₄ – P₁, T₁, R₁, Q₁, затем на П₂ по линиям связи, перпендикулярным х₁₂ – P₂, T₂, R₂, Q₂.

Соединив построенные точки P, T, R, Q прямыми, получим ломаную линию сечения.