2. Определение собственной видимости ребер многогранника

Для определения видимости элементов чертежа используется метод конкурирующих точек. Напомним, что конкурирующими называются точки, лежащие на одной проецирующей прямой.

Рисунок 51

Например, на рис. 51 представлена пара конкурирующих точек 1 и 2, принадлежащих горизонтально-проецирующей прямой. Определим, какая из этих точек видима на горизонтальной плоскости проекций П₁.

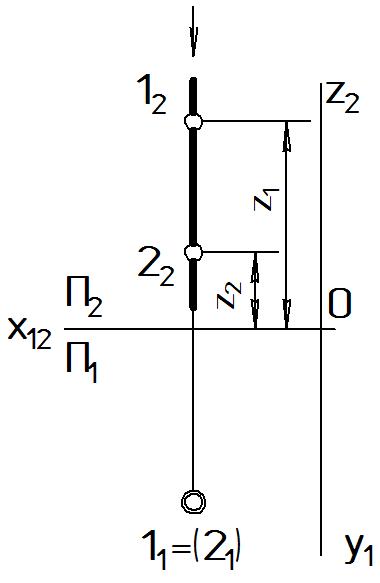
Вопрос о видимости этих точек на П₁, где обе точки проецируются в одну, решается следующим образом: из двух совпадающих проекций конкурирующих точек, лежащих на одной горизонтально-проецирующей прямой видна та, высота (z) которой больше (или видна та точка, которая расположена дальше от П₁ по ходу проецирования, показанного стрелкой). Посмотрим на П₂ высота какой точки больше? Для этого сравним координаты z проекций 1₂ и 2₂. z₁  z₂, то есть высота точки 1 больше. Следовательно, на плоскости П₁ проекция 1₁ видима, невидимую точку (2₁) заключаем в скобки. Действительно по ходу проецирования первой будет получена проекция 2₁, затем 1₁, так как 1₂ расположена дальше от П₁.

Рисунок 52

На рис. 52 представлена пара конкурирующих точек 3 и 4, принадлежащих фронтально-проецирующей прямой. Определим, какая из этих точек видима на фронтальной плоскости проекций П₂.

Вопрос о видимости этих точек на П₂ решается следующим образом: из двух совпадающих проекций конкурирующих точек, лежащих на одной фронтально-проецирующей прямой видна та, глубина (y) которой больше (или видна та точка, которая расположена дальше от П₂ по ходу проецирования, показанного стрелкой).

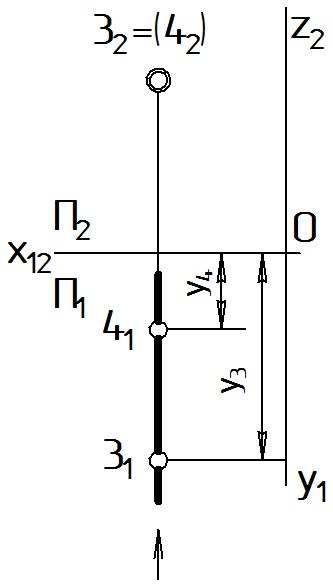
Посмотрим на П₁ глубина какой точки больше? Для этого сравним координаты y проекций 3₁ и 4₁. y₃  y₄, то есть глубина точки 3 больше, следовательно, 3₂ видима, невидимую точку (4₂) заключаем в скобки. Действительно по ходу проецирования первой будет получена проекция 4₂, затем 3₂, так как 3₁ расположена дальше от П₂.

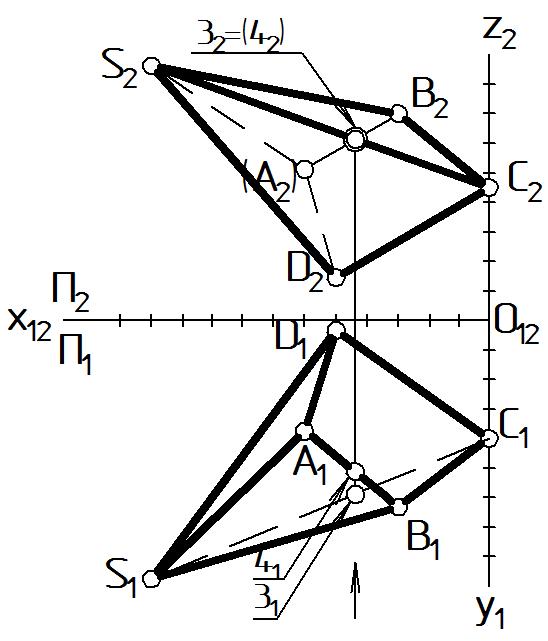
Рассмотрим определение видимости ребер многогранника на примере четырехугольной пирамиды. Порядок определения видимости проекций следующий:

Рисунок 53

Этап 1. Определить видимость очерковых линий.

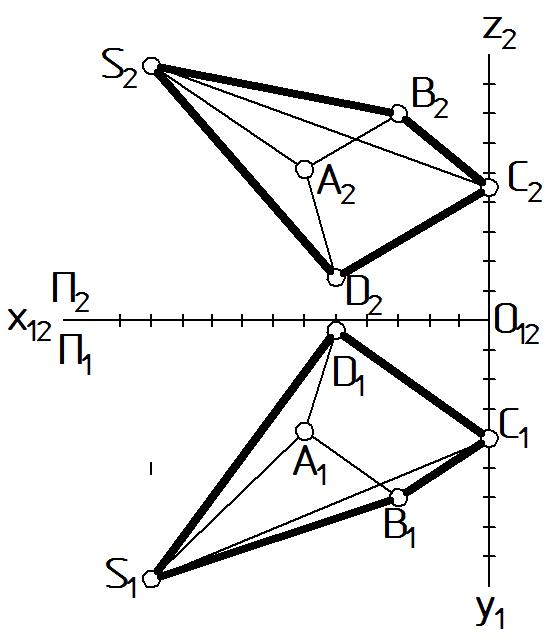
Очерковыми называются линии, по отношению к которым все точки изображаемого объекта расположены по одну сторону. Эти линии видны всегда.

Для пирамиды на П₂ видима фронтальная очерковая S₂ B₂ C₂ D₂ S₂, на П₁ - горизонтальная очерковая S₁ D₁ C₁ B₁ S₁ замкнутые ломаные линии (Рис. 53).

Этап 2. Определить видимость ребер внутри очерка на горизонтальной плоскости проекций П₁.

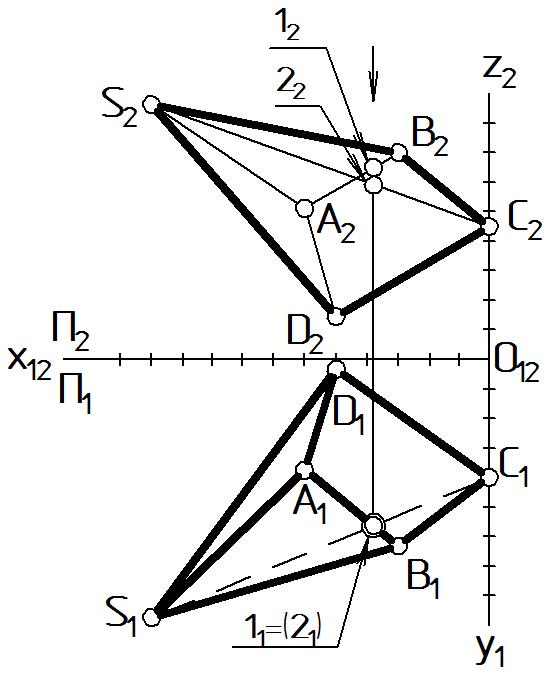
На П₁ возьмем пару конкурирующих точек, принадлежащих скрещивающимся ребрам пирамиды. Пусть 1  [АВ] и 2  [SC]. На П₁ проекции этих точек 1₁ и 2₁ совпадают (Рис. 54).

Рисунок 54

Вопрос видимости для 1₁ и 2₁ решается на П₂, где их проекции разнесены. На П₂ проекция точки 1₂ расположена выше проекции 2₂ (координата z₁ > z₂), следовательно, точка 1 расположена в пространстве выше точки 2 и прикрывает ее собой (см. Рис. 51).

Таким образом, на чертеже в плоскости П₁ видна проекция точки 1₁ и проекция ребра, к которому она относится - [А₁В₁]. Ребро обозначается основной линией. Невидимая на П₁ проекция 2₁ принадлежит ребру [S₁C₁], следовательно это ребро невидимое и обозначается штриховой линией.

Внутри очерка остались ребра [А₁D₁], [S₁A₁], они видимые, поскольку имеют общую с видимым ребром [А₁В₁] вершину A₁.

Рисунок 55

Этап 3. Определить видимость ребер внутри очерка на фронтальной плоскости проекций П₂.

На П₂ возьмем пару конкурирующих точек, принадлежащих скрещивающимся ребрам пирамиды. Пусть 3  [SC] и 4  [АВ]. На П₂ проекции этих точек 3₂ и 4₂ совпадают (Рис. 55). Вопрос их видимости решается на П₁: глубина точки 3₁ больше, чем у 4₁ (координата y₃  y₄), следовательно, точка 3 расположена в пространстве перед точкой 4 и прикрывает ее собой (см. Рис. 52).

По видимости проекций точек определяется видимость соответствующих ребер на П₂. Ребро [S₂C₂] видимое, ребро [А₂В₂] и пересекающиеся с ним в вершине А₂ ребра [А₂D₂], [S₂A₂] – невидимые.

Рисунок 56

Рассмотрим особенности определения видимости ребер на примере треугольной пирамиды (Рис. 56). Порядок определения видимости проекций аналогичный:

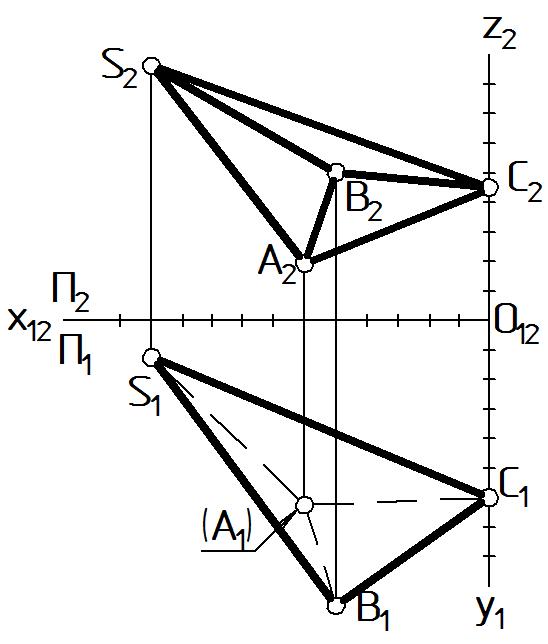
Этап 1. На П₂ видима фронтальная очерковая S₂ C₂ А₂ S₂, на П₁ - горизонтальная очерковая S₁ C₁ B₁ S₁ замкнутые ломаные линии.

Этап 2. Плоскость П₁: внутри очерка нет скрещивающихся ребер, три пересекающиеся ребра [S₁А₁], [C₁А₁], [B₁А₁] будут иметь одинаковую видимость, определяемую видимостью общей вершины А₁. Вопрос видимости для А₁ решается на П₂. Проекция точки А₁ расположена ниже всех вершин пирамиды (координата z_А = min), следовательно, точка А расположена в пространстве ниже точек фигуры, следовательно, А₁ - невидимая .

Этап 3. Плоскость П₂: внутри очерка нет скрещивающихся ребер, три пересекающиеся ребра [S₂В₂], [C₂В₂], [А₂B₂], будут иметь одинаковую видимость, определяемую видимостью общей вершины B₂. Вопрос видимости для B₂ решается на П₁. Проекция точки B₂ имеет наибольшую глубину среди всех вершин пирамиды (координата y_B = max), следовательно, точка B₂ видимая.

Рисунок 57

Для призмы на рис. 57 видимость определяется в том же порядке:

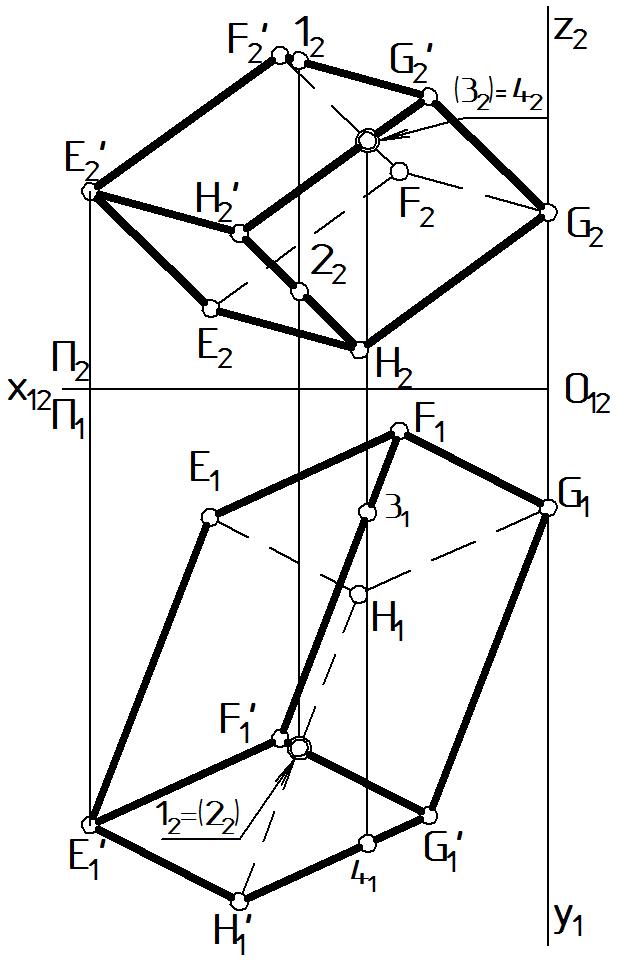
Этап 1. На П₂ видима фронтальная очерковая E₂ E₂’ F₂’ G₂’ G₂ H₂ E₂, на П₁ - горизонтальная очерковая E₁ F₁ G₁ G₁’ H₁’ E₁’ E₁ замкнутые ломаные линии.

Этап 2. Плоскость П₁. На П₁ возьмем пару конкурирующих точек, принадлежащих скрещивающимся ребрам пирамиды. Пусть 1  [E’G’] и 2  [G’H’]. На П₂ проекция точки 1₂ расположена выше проекции 2₂ (координата z₁ > z₂), следовательно, точка 1 расположена в пространстве выше точки 2. Таким образом, на плоскости П₁ видна проекция точки 1₁ и проекция ребра, к которому она относится - [E₁’G₁’]. Видимость остальных ребер понятна из чертежа.

Этап 3. Плоскость П₂.На П₂ возьмем пару конкурирующих точек, принадлежащих скрещивающимся ребрам пирамиды. Пусть 3  [FF’] и 4  [G’H’]. На П₂ проекции этих точек 3₂ и 4₂ совпадают. Вопрос их видимости решается на П₁: глубина точки 4₁ больше, чем у 3₁ (координата y₄  y₃), следовательно, точка 4 расположена в пространстве перед точкой 3 и прикрывает ее собой. По видимости проекций точек определяется видимость соответствующих ребер на П₂. Ребро [G₂’H₂’] видимое. Видимость остальных ребер понятна из чертежа.