Самостоятельная графическая работа Общие требования

Задания на самостоятельную графическую работу (СГР) представлены вариантами. Номер варианта соответствует порядковому номеру студента в алфавитном списке академической группы.

Выполнение СГР рекомендуется выполнять на черновике (бумага в клетку или миллиметровка). Готовая СГР представляется на проверку на ватмане формата А3(297 мм  420 мм), ориентация горизонтальная или вертикальная. На формате оформляется рамка, ограничивающая рабочее поле чертежа (с левой стороны 20 мм от кромки листа, с остальных сторон по 5 мм). В правом нижнем углу рабочего поля вплотную к рамке выполняется основная надпись в виде прямоугольника (185 мм  15 мм), разделенного на три ячейки. В первой ячейке указывается Ф.И.О. автора, во второй ячейке - № группы, в третьей - № варианта. Таблица исходных данных (100 мм  55 мм) размещается в любом углу рабочего поля.

Задачи СГР вычерчиваются в натуральную величину с равномерным заполнением рабочего поля. Все вспомогательные построения сохраняются на чертеже. Допускается частичное наложение различных задач друг на друга.

Чертеж выполняется с применением чертежных инструментов простым карандашом в соответствии с ГОСТ 2.303-68. Проекции точек изображают пустыми окружностями 1,5 мм линией 0,35 мм, проекции конкурирующих точек – двойной окружностью 1,5 мм, 2 мм; оси координат и линии связи проекций показывают линией 0,35 мм; видимые проекции фигур – сплошной линией 0,7 мм; невидимые – штриховой линией 0,35 мм; ось вращения – штрих-пунктирной 0,7 мм; линии сгиба на развертке – штрих-пунктирной с двумя пунктирами 0,35 мм; собирательное свойство следа плоскости показывают утолщенным штрихом 1 мм длиной 10 мм. Параллельность и перпендикулярность прямых отмечается соответствующими знаками.

Все надписи выполняются шрифтом простым карандашом в соответствии с ГОСТ 2.304-81 шрифтом h5 или h3,5. Истинные величины подписываются «и.в.».

План работы

1. Построить двухкартинный комплексный чертеж многогранника и плоскости по заданным координатам точек и геометрическим условиям.

2. Определить собственную видимость ребер многогранника.

3. Построить линию пересечения многогранника заданной плоскостью общего положения.

4. Определить видимость сечения.

5. Определить относительную видимость многогранника и секущей плоскости.

6. Определить истинную величину сечения.

7. Построить развертку многогранника.

8. Перенести на развертку линию сечения.

1. Построение фигур по координатам точек и геометрическим условиям

Любая геометрическая фигура может быть определена в пространстве как совокупность точек, расположение которых друг относительно друга в выбранном пространстве подчиняется некоторым закономерностям. Именно количество координат, позволяющих полностью определить точку в этом пространстве, является важной характеристикой самого пространства, называемой размерностью (R).

При выполнении СГР строится чертеж, т.е. используется двумерное пространство - плоскость для изображения геометрических моделей трехмерных объектов.

Напомним требования к чертежу, он должен быть:

1) обратимым, т. е. давать возможность решения задачи восстановления формы и положения объекта по изображению;

2) наглядным,

3) достаточно простым и точным по выполнению.

В СГР обратимость обеспечивается использованием двухкартинного комплексного чертежа или эпюра, то есть чертежа, полученного на двух совмещенных плоскостях проекций П₁ и П₂ и включающего две проекции объекта.

Наглядность чертежа позволяет оценивать многие геометрические особенности фигур (закономерности взаимного расположения составляющих их точек) визуально. Большую роль при этом играют геометрические условия. Геометрическими условиями являются отношения взаимной принадлежности, параллельности, перпендикулярности, касания, симметрии элементов чертежа. Наглядность так же обеспечивается применением условных обозначений и типов линий.

Простота и точность выполнения обеспечивается применением чертежных инструментов – карандаша, линейки и циркуля.

Итак, при изображении геометрических моделей трехмерных объектов в качестве базового элемента (примитива) используют точку.

В задачах СГР предлагается рассмотреть взаимодействие двух геометрических фигур: плоскости общего положения и многогранника.

Многогранником называют пространственную фигуру, ограниченную замкнутой поверхностью, состоящей из отсеков плоскостей, имеющих форму многоугольников (в частном случае треугольников). Вершины многоугольников образуют вершины многогранника, стороны многоугольников образуют ребра, а плоскости многоугольников — грани многогранника.

Из множества многогранников берутся либо n-гранная призма, либо n-гранная пирамида.

Призма и пирамида выделяются из множества многогранников характеристиками своих граней (законом их образования) и характером их расположения относительно нижнего основания.

Призмой называется многогранник, у которого две грани (основания) n-угольники, остальные n-граней (боковые) параллелограммы. Основания призмы равны и расположены в параллельных плоскостях.

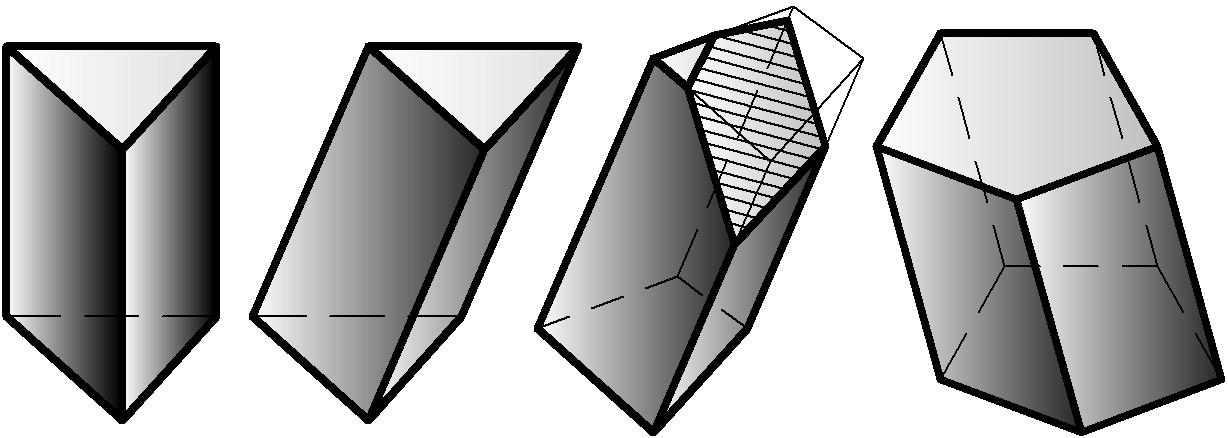
Призму называют прямой (Рис. 46 а), если ее боковые грани перпендикулярны плоскости основания, в противном случае - наклонной (Рис. 46 б).

а б в г

Рисунок 46

Призму называют правильной, если в ее основании лежит правильный многоугольник (Рис. 46 а, б, г).

Призмы классифицируют в соответствии с количеством углов основания - треугольная, четырехугольная, n-угольная.

Часть призмы, отсеченной плоскостью общего положения, называют усеченной призмой (Рис. 46 в).

В задании на СГР координатами своих вершин задается не усеченная наклонная, неправильная треугольная либо четырехугольная призма.

Рассмотрим порядок построения двухкартинного комплексного чертежа призмы.

В начале необходимо подготовить координатные оси x₁₂, y₁, z₂, ограничивающие горизонтальную П₁ и фронтальную П₂ плоскости проекций (см. Рис. 6, Рис. 9 а), проградуировать их делениями по 10 мм.

Точки E, F, G, H - определяют одно из оснований призмы, точки E’, F’, G’, H’ - второе. Точка определена на комплексном чертеже тогда и только тогда, когда заданы две ее проекции ‑ горизонтальная и фронтальная. Следовательно, необходимо построить горизонтальные и фронтальные проекции каждой точки (см. Рис. 9 а и комментарии к нему).

При этом для определения плоскости, которой принадлежит основание, достаточно трех точек. Поэтому три координаты трех точек, например E, F, G, одного из оснований должны быть заданы как основные. В том случае, когда на стороны основания наложены дополнительные геометрические условия (такие, как параллельность сторон), количество координат необходимых для определения точки H сокращается.

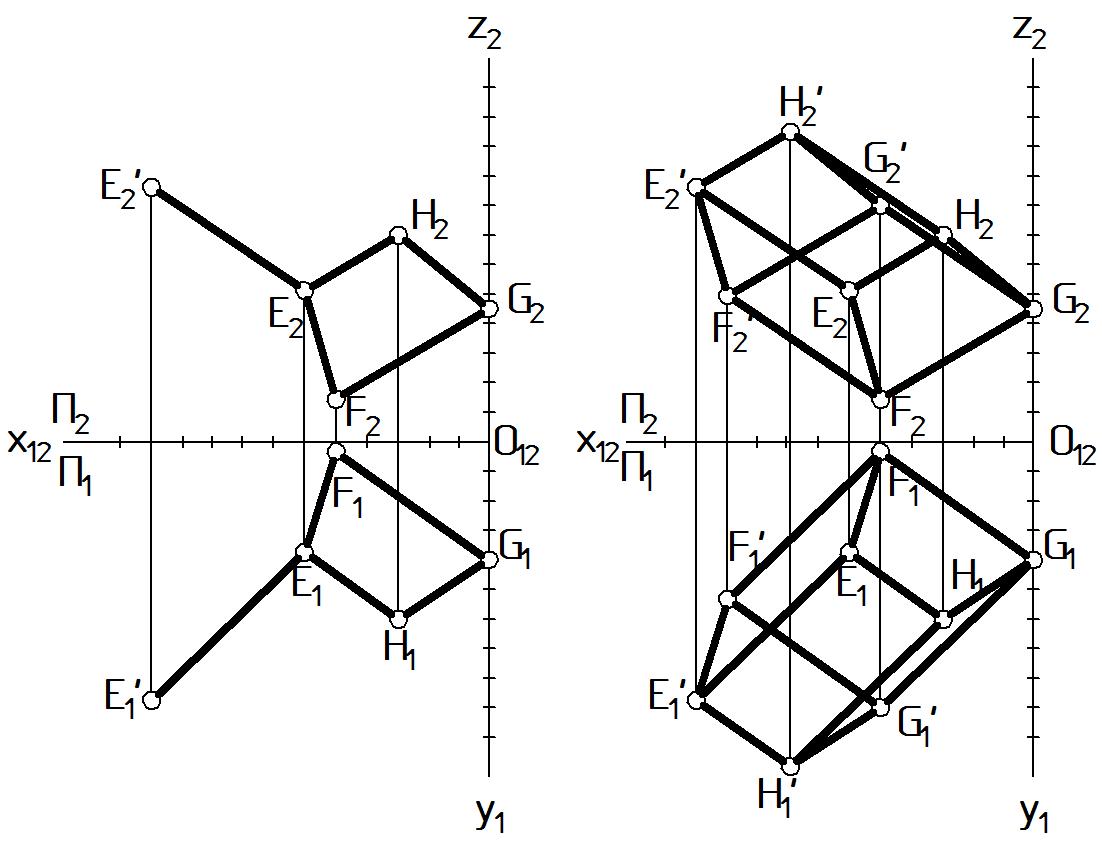
На рис. 47 а приведен двухкартинный комплексный чертеж точек, задающих одно основание призмы EFGH и одна из вершин второго основания E’. Отрезок [E E’] определяет боковое ребро призмы.

а б

Рисунок 47

Для определения второго основания призмы (Рис. 47 б) E’F’G’H’ необходимо использовать следующие геометрические условия:

1. свойство параллельности оснований призмы:

(E’F’ // EF, F’G’ // FG, G’H’ // GH, E’H’ // EH);

2. свойство параллельности боковых ребер призмы:

(EE’ // FF’ // GG’ // HH’).Пирамидой называется многогранник, у которого одна грань (основание) n-угольник, остальные n граней (боковые) треугольники с общей вершиной.

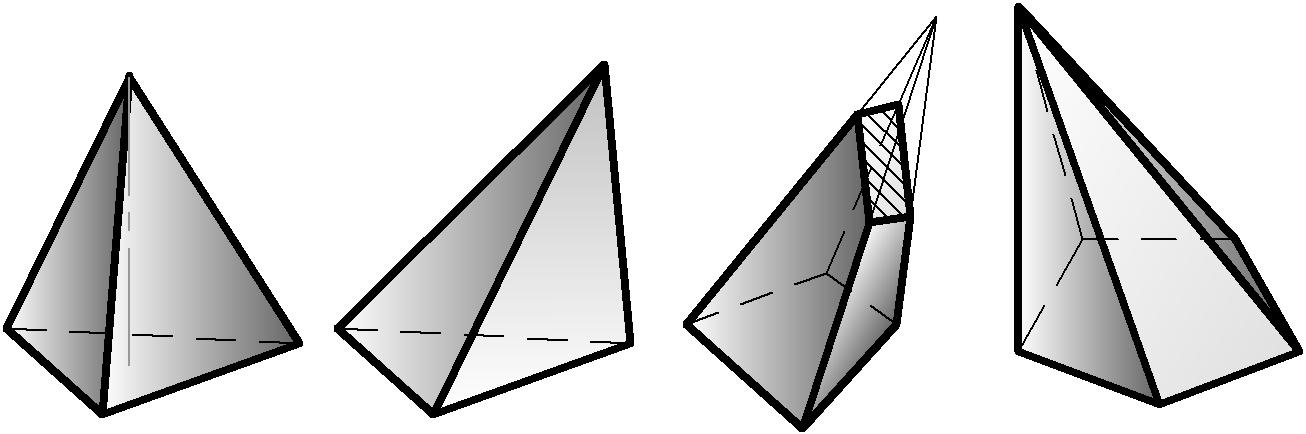
Пирамиду называют правильной, если в ее основании лежит правильный многоугольник и высота проходит через центр основания (Рис. 48 а), в противном случае наклонной (Рис. 48 б)

а б в г

Рисунок 48

Пирамиды классифицируют в соответствии с количеством углов основания - треугольная, четырехугольная, n-угольная (Рис. 48  б, в, г).

Часть пирамиды, отсеченной плоскостью общего положения, называют усеченной пирамидой (Рис. 48 в).

В СГР координатами своих вершин задается не усеченная наклонная неправильная треугольная либо четырехугольная пирамида.

Рассмотрим порядок построения двухкартинного комплексного чертежа пирамиды.

В начале также необходимо подготовить проградуированные координатные оси x₁₂, y₁, z₂, ограничивающие плоскости проекций П₁ и П₂.

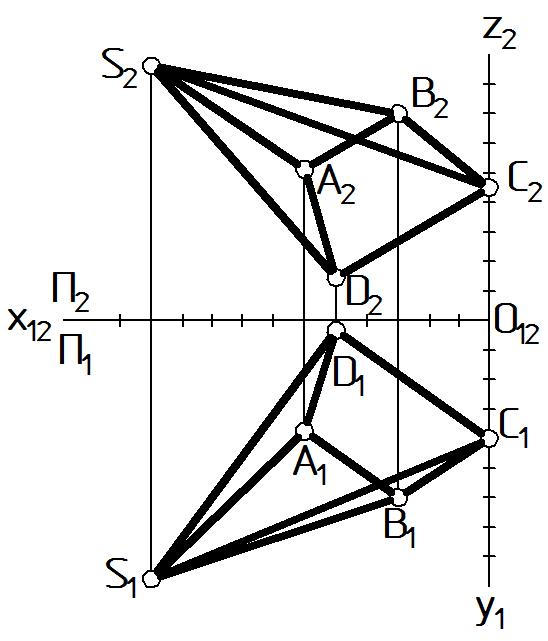
Затем необходимо построить горизонтальные и фронтальные проекции каждой точки. По аналогии с призмой, основание пирамиды однозначно определяется координатами трех точек, например, A, B, C, а для четвертой точки D следует задать две координаты, третья является справочной (Рис. 49).

Если на стороны основания наложены дополнительные условия (например, параллельность сторон AB // CD, BC // AD), то точка D может быть построена по этим геометрическим условиям.

Так как пирамида наклонная, то все три координаты вершины S являются основными.

Рисунок 49

Замечание: ребра как призмы, так и пирамиды на этом этапе рекомендуется выполнить тонкими линиями, поскольку в дальнейшем их видимость будет уточняться.

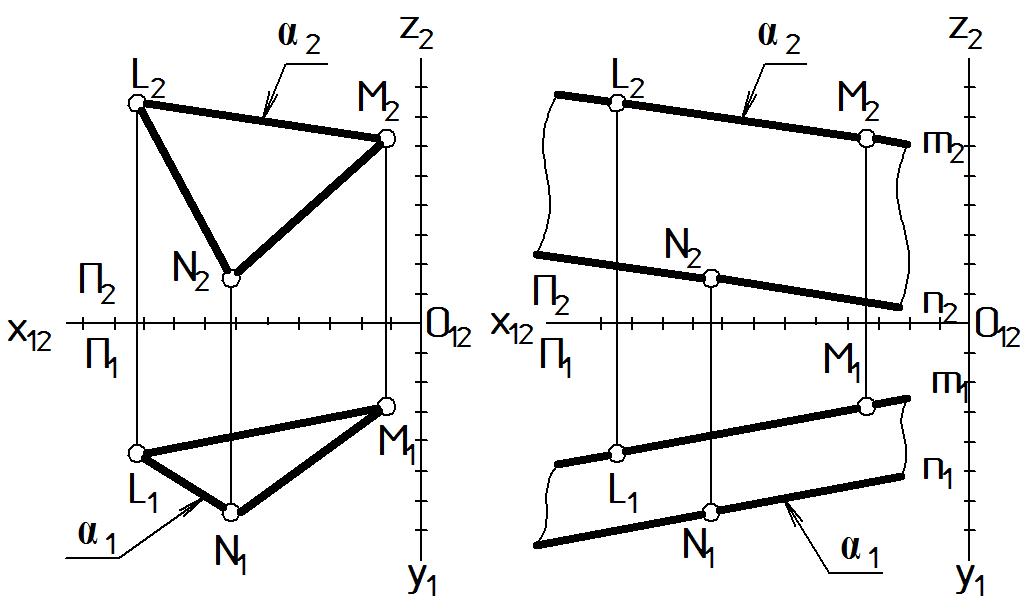
Рассмотрим порядок построения двухкартинного комплексного чертежа плоскости. В СГР плоскость однозначно определяется тремя точками, не лежащими на одной прямой L, M, N и задается ими на чертеже (Рис. 50). Заметим, что чертеж плоскости выполняется в тех же осях, что и многогранник.

а б

Рисунок 50

В зависимости от геометрических условий, плоскость может быть задана:

• треугольником  (LMN). В этом случае проекции следует обозначить отсеками треугольников, соединив соответствующие проекции точек отрезками прямых линий: ₁ (L₁M₁N₁), ₂ (L₂M₂N₂) (Рис. 50 а);

• двумя параллельными прямыми  (m // n), m  L; M, n  N. В этом случае сначала необходимо построить проекции соответствующих фрагментов прямых m и n, затем обозначить отсеки, соединив соответствующие концы прямых волнистыми линиями обрыва: ₁ (m₁ // n₁), ₂ (m₂ // n₂) (Рис. 50 б).