Способ вращения вокруг проецирующей прямой

При решении задач этим способом пространственный объект (оригинал) меняет свое положение в пространстве путем поворота относительно некоторой оси вращения так, чтобы объект оказался в каком-либо частном положении (параллельном или перпендикулярном) по отношению к заданным плоскостям проекций. При этом необходимо выполнять следующие условия:

• ось вращения – прямая перпендикулярная одной из плоскостей проекций;

• каждая точка перемещаемой фигуры перемещается по окружности в плоскости вращения, перпендикулярной оси вращения.

Рисунок 43

Рассмотрим примеры вращения. Дана точка А и две ее проекции А₁, А₂ , полученные ортогональным проецированием на плоскости П₁ и П₂ (Рис. 43).

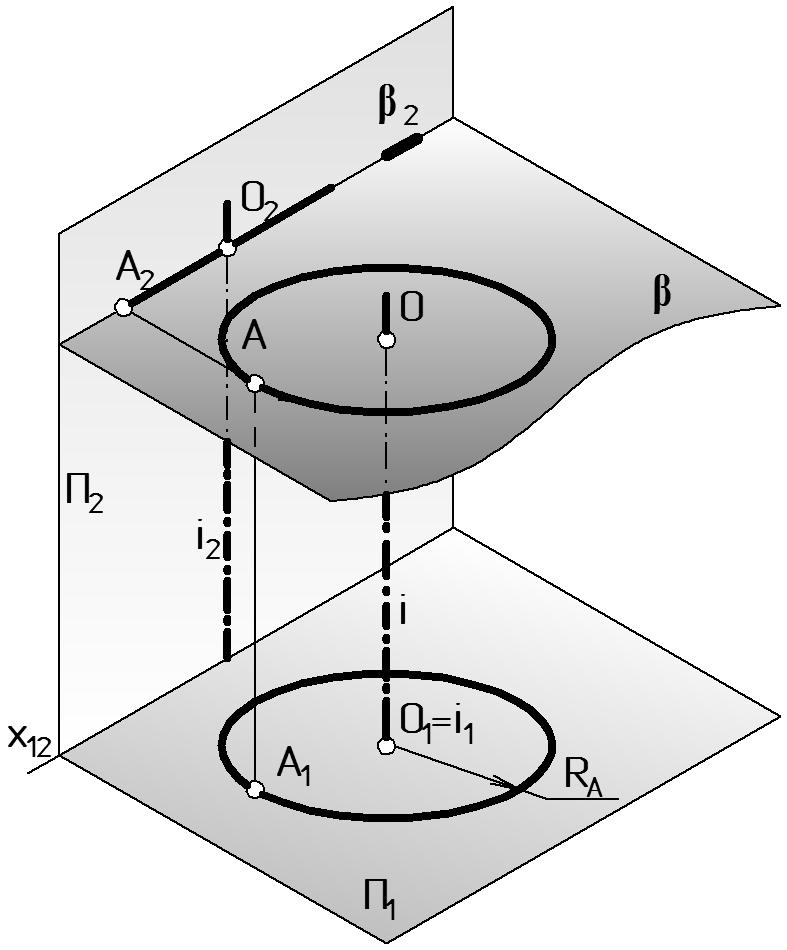
Пусть точка А вращается вокруг некоторой оси вращения i, перпендикулярной к плоскости П₁. При вращении точка А описывает окружность с центром О в плоскости , перпендикулярной оси вращения i. Так как  // П₁, то окружность проецируется на П₁ в истинную величину, при этом R = О₁А₁. Так как   П₂, то окружность проецируется на П₂ отрезком прямой, длиной 2R, полностью совпадающим со следом плоскости ₂.

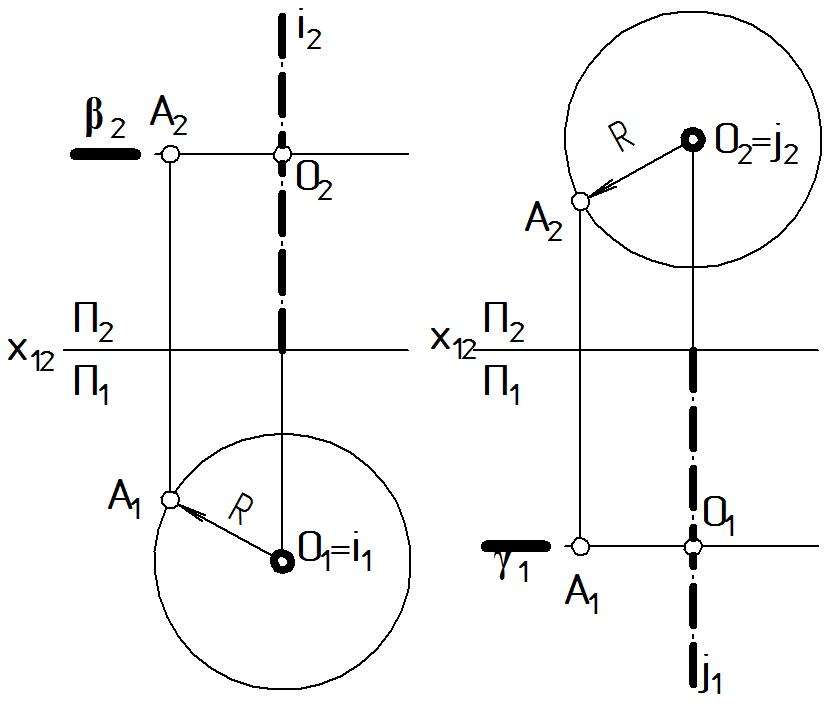
Соответствующий чертеж выполняют в следующем порядке (Рис. 44 а):

• выбирают положение оси вращения i (i₁; i₂)  П₁ относительно объекта А (в данном случае выбор произволен);

• горизонтальная проекция А₁ перемещается по окружности радиуса, равного расстоянию от точки А до оси i: R = О₁А₁;

• фронтальная проекция А₂ перемещается в горизонтальной плоскости уровня  // П₁ по окружности, которая полностью совпадает со следом плоскости ₂  i₂, поэтому изображается отрезком прямой длиной 2R.

а б Рисунок 44

На рис. 44 б показано вращение точки А вокруг фронтально проецирующей прямой j (j₁; j₂)  П₂:

• горизонтальная проекция А₁ перемещается во фронтальной плоскости уровня  // П₁, по окружности, совпадающей со следом плоскости ₁  j₁, изображается отрезком прямой длиной 2R.

• фронтальная проекция А₂ перемещается по окружности радиуса R = О₂А₂.

Рассмотрим применение вращения для решения задач.

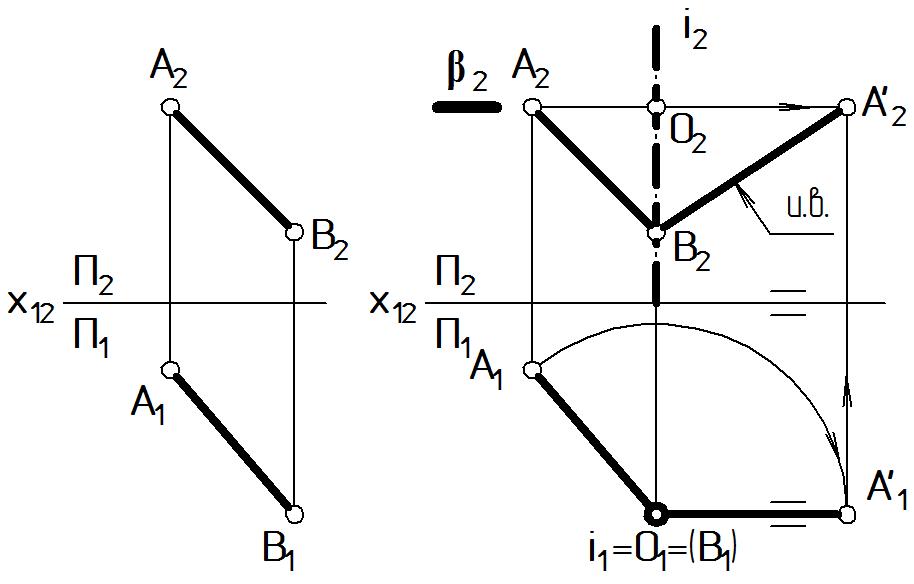
Задача 3. Нахождение истинной величины отрезка АВ, занимающего общее положение (Рис. 45).

Дано: АВ - о.п. (Рис. 45 а). Найти: и.в. АВ.

Решение. Задача решается поворотом отрезка вокруг оси на такой угол, чтобы после поворота отрезок занял частное положение, например, параллельное плоскости П₂: АВ - о.п.  А’В’ // П₂.

а б Рисунок 45

Соответствующий чертеж выполняют в следующем порядке:

• выбирают положение оси вращения i (i₁; i₂)  П₁ так, чтобы она проходила через одну из точек вращаемого отрезка, например, i  В. В этом случае точка В не будет менять своего положения;

• горизонтальная проекция А₁ перемещается по дуге окружности радиуса R = О₁А₁ по часовой стрелке до тех пор, пока вращающийся отрезок не займет частное положение, например, параллельное плоскости П_2. Полученную проекцию точки индексируют А’₁: А’₁В₁ // x₁₂;

• фронтальная проекция А₂ перемещается вправо по окружности, полностью совпадающей со следом плоскости ₂  i₂, поэтому отображается в виде горизонтальной прямой;

• для нахождения точки А’₂ необходимо из А’₁ восставить линию связи, перпендикулярную x₁₂, и отметить точку ее пересечения со следом плоскости ₂;

• соединив проекции А’₂, В₂, получим изображение А’₂В₂.

• В соответствии с инвариантным свойством проецирования 7) если фигура параллельна плоскости проекций П₂, то проекция фигуры на П₂ равна истинной величине: А’₂В₂ = и.в. АВ.