Некоторые метрические задачи

Задачи, решение которых связано с нахождением истинной величины и формы геометрических фигур, расстояния между ними и другие характеристики по их метрически искаженным проекциям, называются метрическими.

В основе алгоритма решения любой метрической задачи лежит 7) инвариантное свойство ортогонального проецирования, заключающееся в том, что если фигура принадлежит плоскости , параллельной плоскости проекций П₁, то проекция фигуры на П₁ равна истинной величине.

Определение истинной величины отрезка прямой по методу прямоугольного треугольника

На комплексном чертеже ни одна из проекций отрезка прямой общего положения не может быть равна истинной его величине.

а б

Рисунок 36

Рассмотрим рис. 36 а, на котором показан отрезок [АВ] общего положения и его проекция [А₁В₁] на горизонтальную плоскость проекций П₁.

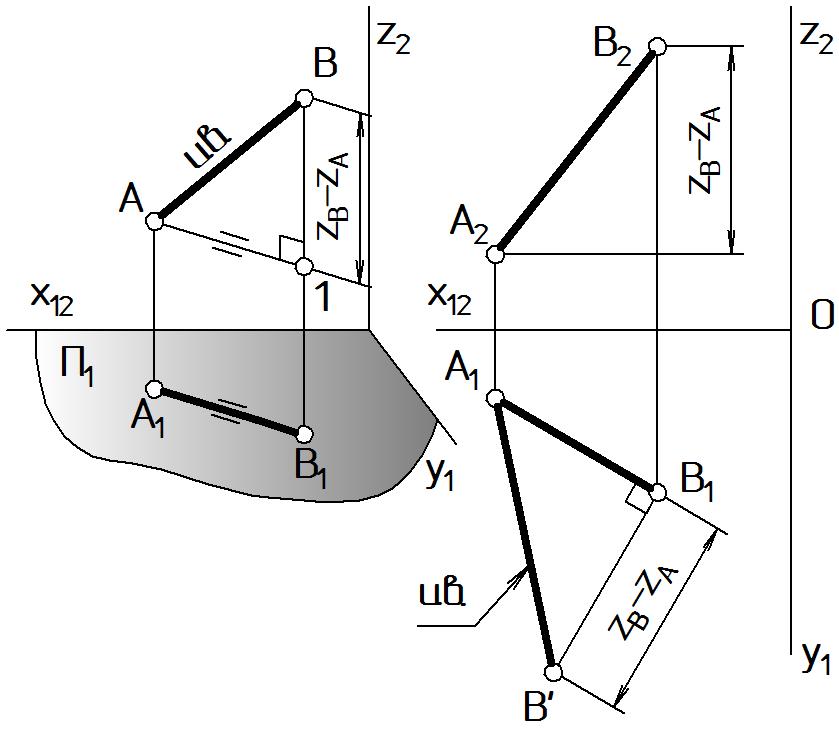
Фигура А₁АВВ₁, образованная при проецировании, ‑ прямоугольная трапеция, наклонной стороной которой является отрезок [АВ], высотой ‑ его горизонтальная проекция [А₁В₁], основаниями ‑ горизонтально-проецирующие прямые [AA₁] и [ВВ₁].

Если провести прямую [1А] // [А₁В₁], то от трапеции А₁АВВ₁ отсечется прямоугольный треугольник 1АВ с гипотенузой [АВ]. Один катет [1A] = [А₁В₁]. Другой катет [1В] равен разности координат z_B и z_A, то есть разности длин прямых, проецирующих концы отрезка [АВ] на плоскость П₁ ([1В] = [ВВ₁] – [АА₁] = z_B - z_A).

На комплексном чертеже (Рис. 36 б) этот прямоугольный треугольник строится на плоскости П₁ непосредственно на горизонтальной проекции отрезка [А₁В₁]. От любого конца этого отрезка откладывается прямой угол (на рис. 36 б реализован один из 4 возможных вариантов: от точки В₁ вниз).

В качестве второго катета берется отрезок [В₁В’] = z_B - z_A , длина которого определяется на П₂. Гипотенуза [A₁B’] равна истинной величине отрезка АВ.

Ту же задачу по определению истинной величины отрезка можно решить на плоскости П₂, если в качестве первого катета взять фронтальную проекцию отрезка [А₂В₂], а в качестве второго катета [В₂В”] = y_B - y_A . Гипотенуза [A₂B”] будет равна истинной величине отрезка АВ.

Можно сформулировать общее правило прямоугольного треугольника: истинная (натуральная) величина отрезка прямой определяется гипотенузой прямоугольного треугольника, одним из катетов которого является одна из проекций отрезка, а вторым ‑ разность расстояний от концов другой проекции отрезка до плоскости проекций.

Способы преобразования комплексного чертежа

Решение позиционных и метрических задач упрощается, если пространственный объект занимает частное положение по отношению к плоскостям проекций. Способы преобразования комплексного чертежа позволяют переходить от произвольных положений пространственных объектов, наиболее часто встречающихся в практике, к частным положениям их по отношению к плоскостям проекций.

Способ замены плоскостей проекций

При решении задач этим способом пространственный объект (оригинал) не меняет своего положения в пространстве, а данная система плоскостей проекций заменяется новой так, чтобы объект оказался в каком-либо частном положении (параллельном или перпендикулярном) по отношению к новым плоскостям проекций. При этом необходимо выполнять следующие условия:

• каждая новая система является системой двух взаимно-перпендикулярных плоскостей;

• на новую плоскость проекций объект проецируется ортогонально.

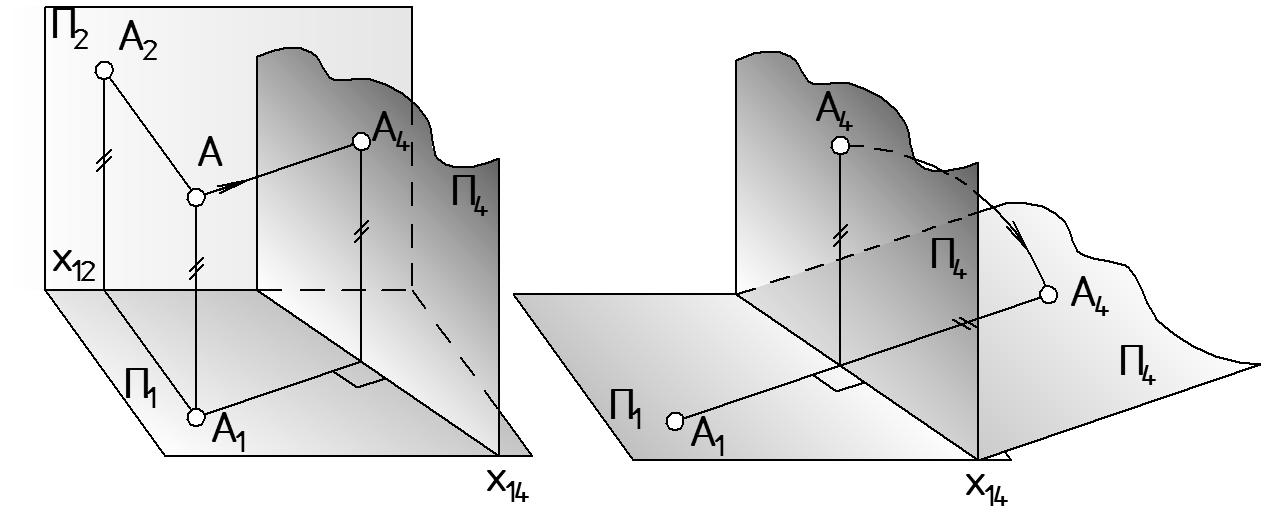
Рассмотрим примеры замены плоскости проекций. Пусть дана точка А и две ее проекции А₁, А₂ , полученные ортогональным проецированием на плоскости П₁ и П₂ (Рис. 37 а).

а б

Рисунок 37

Заменим фронтальную плоскость П₂ на новую плоскость П₄ (П₂  П₄), так, чтобы П₄ была перпендикулярна П₁, которая останется без изменений. При выполнении этого условия положение плоскости П₄ однозначно определится осью х₁₄ = П₁  П₄. Спроецируем ортогонально точку А на П_4, получим новую проекцию А₄. Высота точки А, следовательно, и высота проекции А₄ остается неизменной (z_A = const, на рис. 37 это отмечено штрихами).Для получения комплексного чертежа повернем плоскость П₄ на 90° вокруг оси х₁₄, тем самым совместим ее с плоскостью П₁ (Рис. 37 б). На чертеже, полученном на совмещенных плоскостях, две проекции A₁ и A₄ располагаются на общей линии связи, перпендикулярной к оси х₁₄.

Рисунок 38

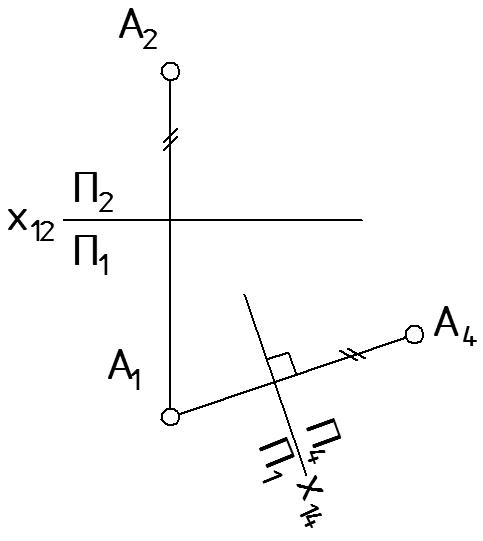
Соответствующий комплексный чертеж выполняют в следующем порядке (Рис. 38):

• на плоскости П₁ выбирают новое положение оси х₁₄ (в данном случае выбор расположения плоскости П₄, следовательно и оси х₁₄ произволен);

• проводят линию связи от точки А₁ перпендикулярно новой оси х₁₄;

• откладывают от оси х₁₄ высоту точки z_A, взятую с плоскости П₂ (z_A = const, на рис. 38 это отмечено штрихами), полученную проекцию индексируют A₄.

Аналогично можно провести замену плоскости П₁ на П₅ (П₁  П₅), так, чтобы П₅ была перпендикулярна П₂, которая остается без изменений.

Рисунок 39

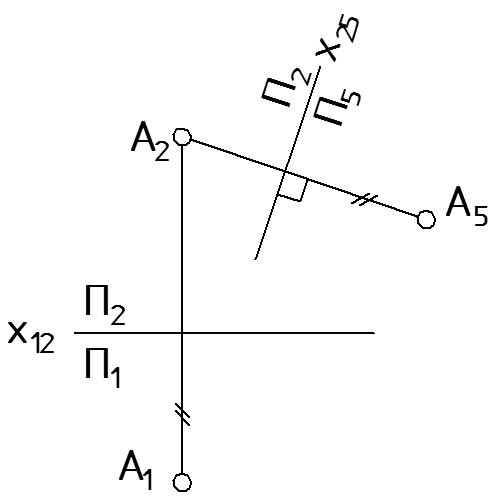
Соответствующий комплексный чертеж выполняют в следующем порядке (Рис. 39):

• на плоскости П₂ выбирают новое положение оси х₂₅ (в данном случае выбор произволен);

• проводят линию связи от точки А₂ перпендикулярно новой оси х₂₅;

• откладывают от оси х₂₅ глубину точки y_A, взятую с плоскости П₁ (y_A = const, на рис. 39 это отмечено штрихами), полученную проекцию индексируют A₅.

Из рассмотренного выше следуют основные положения способа перемены плоскостей проекций:

1. Новая плоскость проекций всегда выбирается перпендикулярно одной из старых плоскостей проекций;

2. Взаимное положение новой плоскости проекций и фигуры зависит от цели преобразования;

3. Новая проекция точки и незаменяемая проекция точки располагаются на общей линии связи, перпендикулярной новой оси;

4. Расстояние от новой оси до новой проекции точки равно расстоянию от заменяемой проекции точки до старой (предыдущей) оси.

Рассмотрим применение замены плоскости проекций для решения задач.

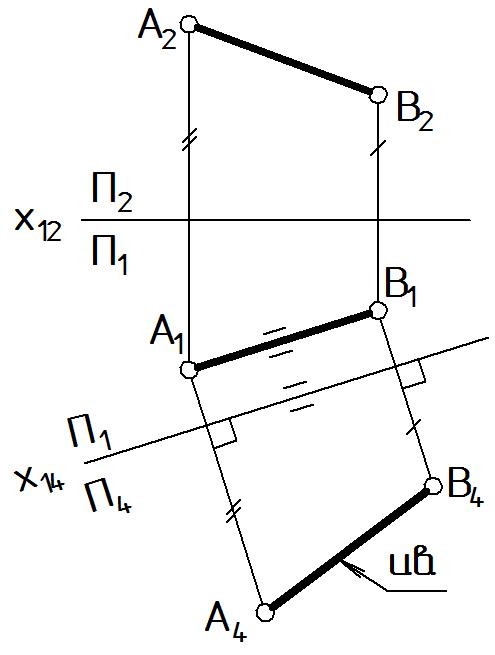
Задача 1. Нахождение истинной величины отрезка АВ, занимающего общее положение (Рис. 40).

Дано: АВ - о.п. Найти: и.в. АВ.

Решение. При выборе взаимного положения новой плоскости проекций и отрезка воспользуемся 7) инвариантным свойством ортогонального проецирования, из которого следует, что если отрезок параллелен П₄, то проекция на эту плоскость равна истинной величине.

Рисунок 40

Заменим фронтальную плоскость П₂ на новую фронтальную плоскость П₄ (П₂  П₄), так, чтобы П₄ оказалась параллельна АВ и перпендикулярна П₁. Положение плоскости П₄ однозначно определится осью х₁₄ = П₁  П₄.

Соответствующий комплексный чертеж выполняют в следующем порядке (Рис. 40):

• на плоскости П₁ выбирают новое положение оси х₁₄. Ось х₁₄ мы теперь не можем проводить произвольно. Чтобы отрезок АВ и плоскость П₄ оказались параллельны (см. рис.13), необходимо х₁₄ провести параллельно горизонтальной проекции отрезка: х₁₄ // А₁В₁. Заметим, что расстояние между А₁В₁ и х₁₄ может быть выбрано произвольно;

• проводят линии связи от точки А₁ и В₁ перпендикулярно оси х₁₄;

• откладывают от оси х₁₄ высоты точек z_A, z_B взятые с плоскости П₂ (это отмечено штрихами), полученные проекции индексируют A₄, В₄;

• соединив проекции А₄, В₄ в отрезок, получим его изображение в истинную величину.

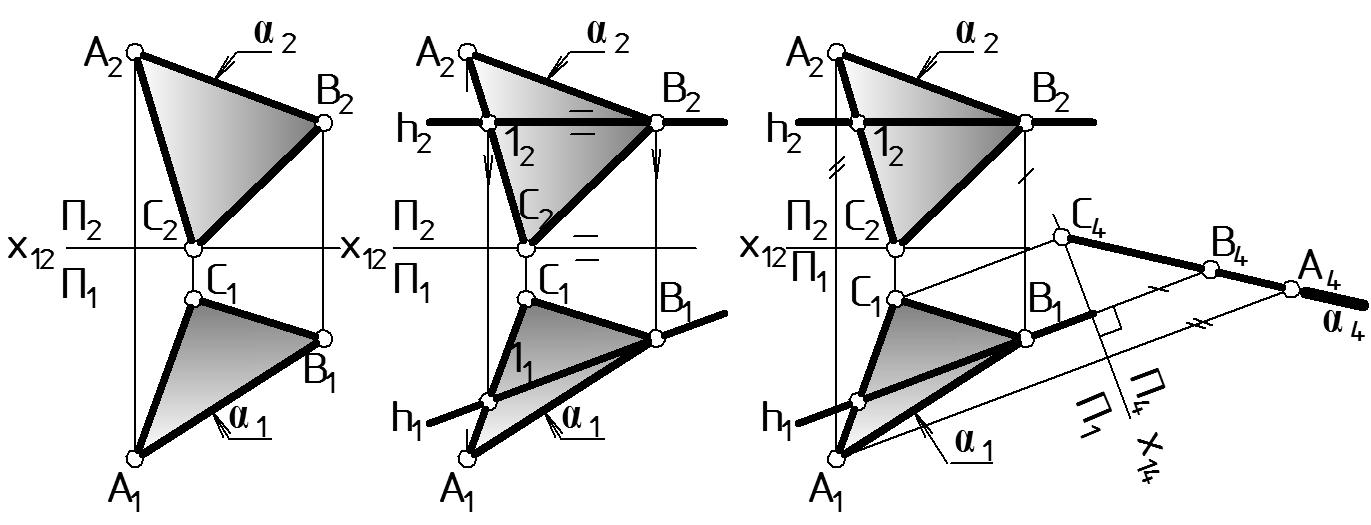
Задача 2. Нахождение истинной величины отсека плоскости  (АВС), занимающей общее положение (Рис. 41).

Дано:  (АВС) - о.п (Рис. 41 а). Найти: и.в. АВС.

а б в

Рисунок 41

Решение: Задача решается последовательной переменой двух плоскостей проекций. Первой переменой П₂  П₄ плоскость  превращается в проецирующую плоскость  (АВС) - о.п.   (АВС)  П₄. Второй переменой П₁  П₅ плоскость  превращается в плоскость уровня  (АВС)  П₄   (АВС) // П₅.

Рассмотрим первое преобразование (Рис. 41 б и Рис. 41 в). Заменим фронтальную плоскость П₂ на новую фронтальную плоскость П₄ (П₂  П₄), так, чтобы П₄ оказалась перпендикулярна  и перпендикулярна П₁. Положение плоскости П₄ однозначно определится осью х₁₄ = П₁  П₄.

Соответствующий комплексный чертеж выполняют в следующем порядке:

• строят проекции горизонтали плоскости h   (АВС) (Рис. 41 б) (порядок построения горизонтали плоскости показан на рис. 27, рис. 30 а).

Замечание: В качестве опорной прямой вместо горизонтали h можно использовать фронталь f плоскости, решение при этом будет соответствовать замене П₁  П₄;

• на плоскости П₁ выбирают положение оси х₁₄. Чтобы  (АВС)  П₄, необходимо х₁₄ провести перпендикулярно горизонтальной проекции горизонтали плоскости h₁: х₁₄  h₁ Расстояние между ₁ и х₁₄ может быть выбрано произвольно (Рис. 41 в);

• проводят линии связи от точек А₁, В₁, С₁ перпендикулярно новой оси х₁₄ (Рис. 41 в);

• откладывают от оси х₁₄ высоты точек z_A, z_B, z_с, взятые с плоскости П₂ (это отмечено штрихами). В данном примере высота точки С z_С=0, поэтому и С₂ и С₄ лежат на соответствующих осях, полученные проекции индексируют A₄, В₄, С₄;

• соединив проекции A₄, В₄, С₄, получим изображение плоскости ₄. В соответствии с инвариантным свойством проецирования 6) если фигура перпендикулярна плоскости проекций П₄, то проекция фигуры полностью совпадает с следом плоскости: (А₄В₄С₄)  ₄.

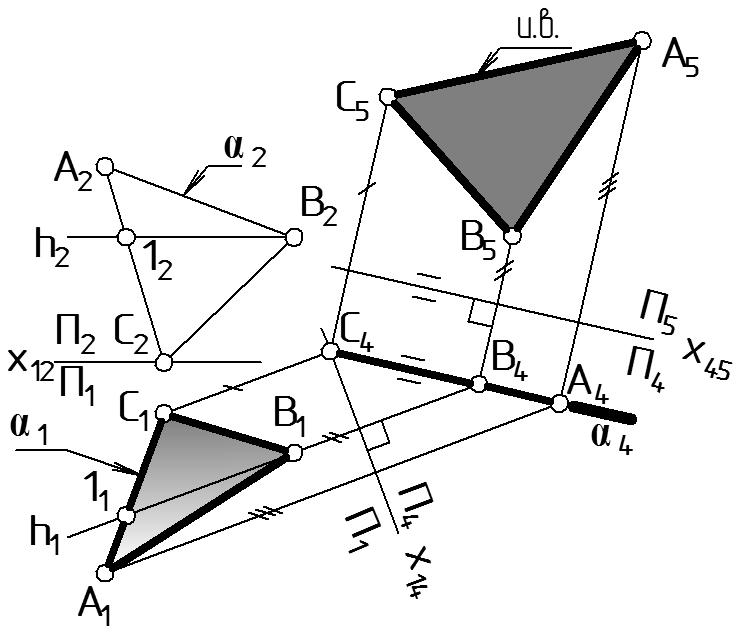
Рисунок 42

Рассмотрим второе преобразование (Рис. 42). Плоскость П₂ и соответствующая проекция ₂ в этом этапе решения не участвует, поэтому показана тонкими линиями.

Заменим горизонтальную плоскость П₁ на новую горизонтальную плоскость П₅ (П₁  П₅), так, чтобы П₅ оказалась параллельна  и перпендикулярна П₄. Положение плоскости П₅ однозначно определится осью х₄₅ = П₄  П₅.

Соответствующий комплексный чертеж выполняют в следующем порядке:

• на плоскости П₄ выбирают положение оси х₄₅. Чтобы  (АВС) // П₅, необходимо х₄₅ провести параллельно проекции плоскости ₄ на произвольном расстоянии: х₄₅ // ₄ (Рис. 42);

• проводят линии связи от точек A₄, В₄, С₄ перпендикулярно новой оси х₄₅;

• откладывают от оси х₄₅ глубины точек y_A, y_B, y_C взятые с плоскости П₁ (это отмечено штрихами). Заметим, что глубины точек y_A, y_B, y_C равны расстоянию от заменяемых проекций точек A₁, В₁, С₁ до предыдущей оси х₁₄ (ось х₁₂ в этом этапе задачи не участвует), полученные проекции индексируют A₅, В₅, С₅;

• соединив проекции A₅, В₅, С₅, получим изображение плоскости ₅. В соответствии с инвариантным свойством проецирования 7) если фигура параллельна плоскости проекций П₅, то проекция фигуры на П₅ равна истинной величине: А₅В₅С₅ = и.в. АВС.