Линии уровня плоскости

Линии уровня плоскости – это прямые, лежащие в данной плоскости и параллельные одной из основных плоскостей проекций. Они имеют специальные названия: горизонталь, фронталь, профильная прямая плоскости.

Горизонталь h – это линия параллельная горизонтальной плоскости проекций П₁, фронталь f параллельна фронтальной плоскости проекций П₂, профильная прямая р параллельна профильной плоскости проекций П₃.

При построении этих прямых следует руководствоваться условиями инцидентности, описанными выше.

Замечание: здесь и далее границы рассматриваемых плоскостей в большинстве случаев ограничиваться не будут.

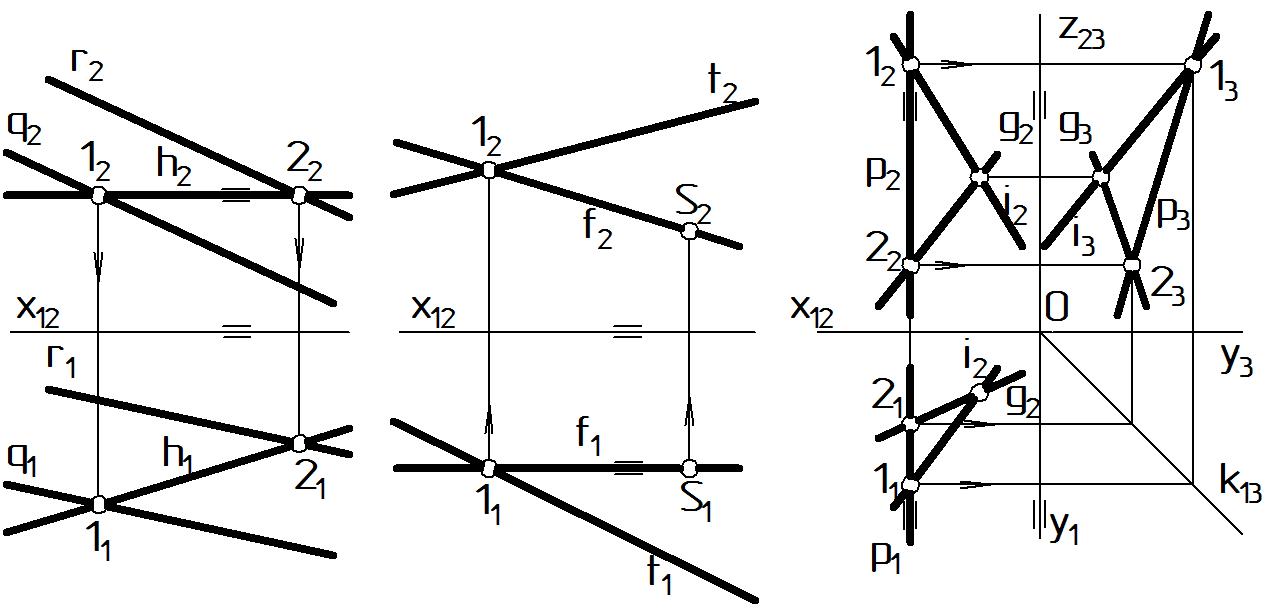
На рис. 30 а показано, как следует строить горизонталь h, принадлежащую плоскости (r  q). Фронтальная проекция любой горизонтали (см. рис. 12) представляет собой горизонтальную линию на чертеже, поэтому горизонталь строят, начиная с фронтальной проекции h₂ на П₂: h₂  х₁₂. Находят точки пересечения h₂ с двумя прямыми r и q, принадлежащими плоскости (r  q): 1₂ = h₂  q₂, 2₂ = h₂  r₂. По линиям связи находят горизонтальные проекции этих точек на П₁ как принадлежащие одноименным прямым: 1₁  q₁, 2₂  r₁. После чего, соединяя 1₁ и 2₁ прямой, получают горизонтальную проекцию горизонтали: h₁=(1₁2₁).

На рис. 30 б показано, как следует строить фронталь f, принадлежащую плоскости (t; S). Фронталь строят, начиная с горизонтальной проекции f₁ на П₁, так как горизонтальная проекция любой фронтали – это горизонтальная линия на чертеже: f₁  х₁₂. В данном случае f₁ необходимо провести через точку S₁, заведомо принадлежащую плоскости (t; S). Другую искомую точку 1₁ находят на пересечения фронтали с прямой t, принадлежащей плоскости: 1₁ = f₁  t₁. По линии связи находят фронтальную проекцию этой точки на П₂: 1₂  t₂. После чего, соединяя 1₂ , S₂ прямой, получают фронтальную проекцию фронтали: f₂=(1₂S₂).

(r  q) (t; S) (g  i) а б в Рисунок 30

На рис. 30 в показано, как следует строить профильную прямую р, принадлежащую плоскости (g  i). Профильную прямую можно строить, начиная с горизонтальной проекции р₁ на П₁ или фронтальной проекции на р₂ на П₂, так как обе эти проекции – это вертикальные линии на чертеже: р₁  y₁, р₂  z₂₃. Находят точки пересечения р₁ с двумя линиями g и i: 1₁ = р₁  i₁, 2₁ = p₁  g₁. По линии связи находят фронтальные проекции этих точек на П₂: 1₂ = р₂ i₂, 2₂ = p₂  g₂. Соединяя 1₂, 2₂ прямой, получают фронтальную проекцию профильной прямой: р₂=(1₂2₂). Затем по ломаным линиям связи находят профильные проекции точек на П₃: 1₃ = р₃  i₃, 2₃ = p₃  g₃. Соединяя точки 1₃ , 2₃ прямой, получают профильную проекцию: р₃ = (1₃2₃).

Задачи пересечения

Задача 1. Нахождение точки пересечения двух прямых (см. Рис. 16 б).

При построении точки пересечения двух прямых следует руководствоваться положением: если прямые пересекаются, то проекции точек пересечения их одноименных проекций лежат на общей линии связи.

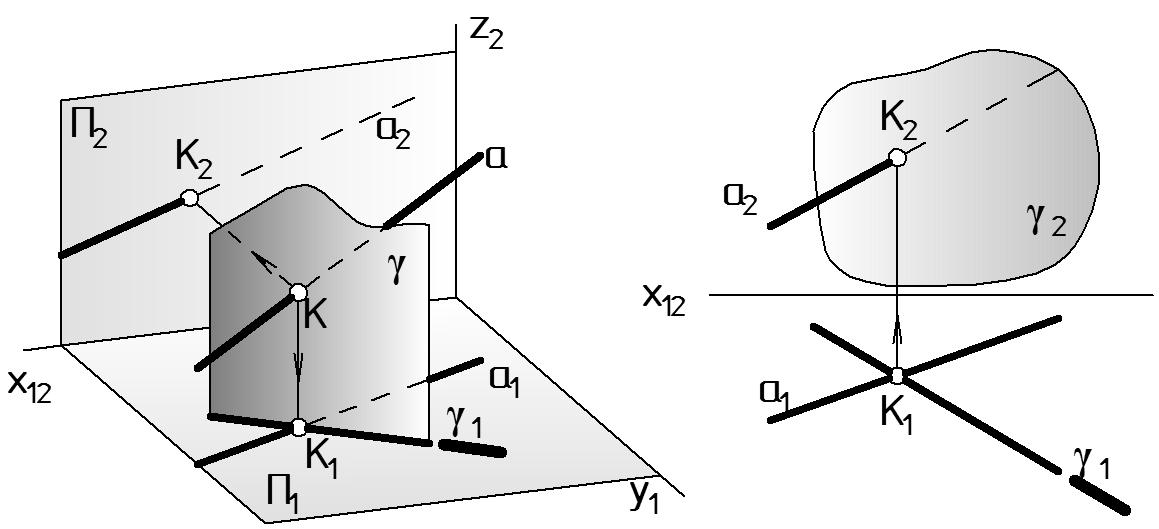
Задача 2. Нахождение точки пересечения прямой общего положения и плоскости, занимающей проецирующее положение (Рис. 31).

Дано: a - о.п.; ( ₁ )  П₁. Найти: K = a  ( ₁ ). Определить видимость.

Решение. Точка пересечения К должна одновременно принадлежать прямой а и плоскости . В соответствии с инвариантным свойством проецирования 6) если фигура принадлежит плоскости, перпендикулярной плоскости проекций П₁, то проекция фигуры совпадает с линией пересечения плоскости с плоскостью П₁, — следом плоскости. Поэтому горизонтальная проекция К₁ (Рис. 31 б) совпадает с горизонтальным следом плоскости ₁: К₁ = ₁  а₁. Фронтальная проекция точки находится по линии связи (К₂  а₂).

а б Рисунок 31

Определим видимость прямой а относительно плоскости . На П₁ проекция прямой видима полностью. На П₂ правая часть прямой находится за плоскостью .

Замечание: Плоскость считается непрозрачной, прямая, находящаяся за плоскостью по направлению проецирования, невидима. Видимые части прямой показывают сплошными, а невидимые – штриховыми тонкими линиями.

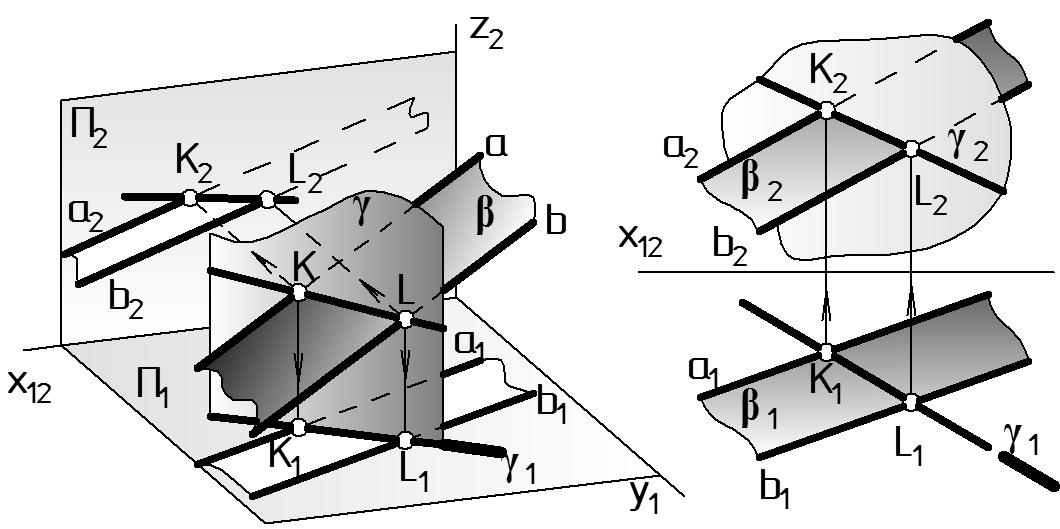
Задача 3. Нахождение линии пересечения плоскости общего положения и плоскости, занимающей проецирующее положение (Рис. 32).

Дано: (а  b) - о.п.; ( ₁ )  П₁. Найти: (KL) =   . Определить видимость.

Решение. Для построения будущей линии пересечения двух плоскостей необходимо построить две точки К и L, каждая из которых должна одновременно принадлежать обеим плоскостям. Искомая прямая принадлежит горизонтально-проецирующей плоскости, следовательно, горизонтальная проекция (К₁L₁) совпадает с горизонтальным следом плоскости: К₁ = ₁  а₁; L₁ = ₁  b₁ (Рис. 32 б). Фронтальные проекции точек строятся по линиям связи: К₂  а₂; L₂  b₂. Проводим через К₂; L₂ фронтальную проекцию линии пересечения плоскостей.

а б
Рисунок 32

Аналогично предыдущей задаче на П₁ проекция ₁ (а₁  b₁) видима полностью. На П₂ правая часть плоскости ₂ (а₂  b₂) находится за плоскостью , не видима.

Задача 4 (Первая позиционная задача). Нахождение точки пересечения прямой общего положения с плоскостью общего положения.

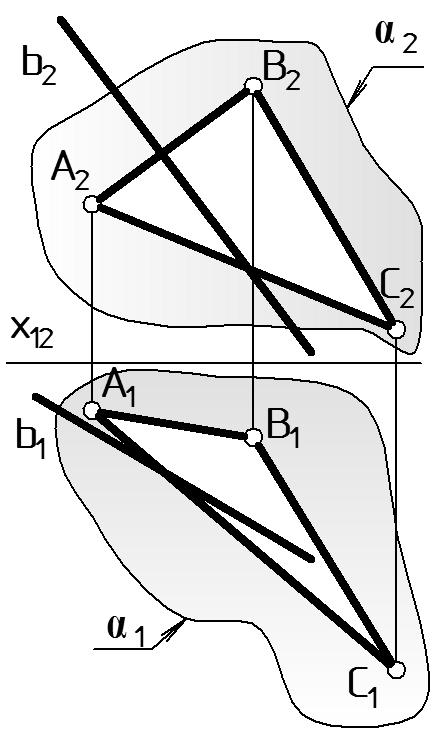
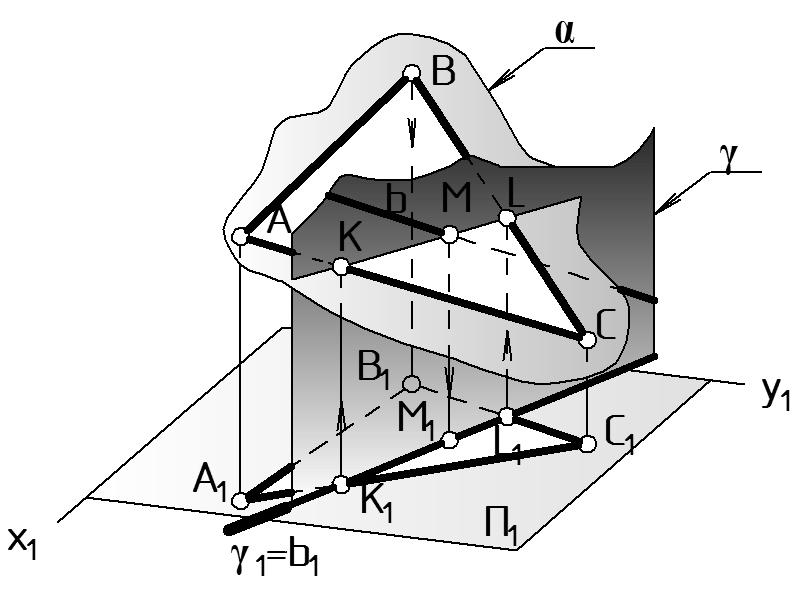
Дано: b - о.п.;  (АВС) - о.п. (Рис. 33 а). Найти: M = b  . Определить видимость.

а б Рисунок 33

Решение. Алгоритм решения включает три этапа, результат которых наглядно показан на Рис. 33 б.

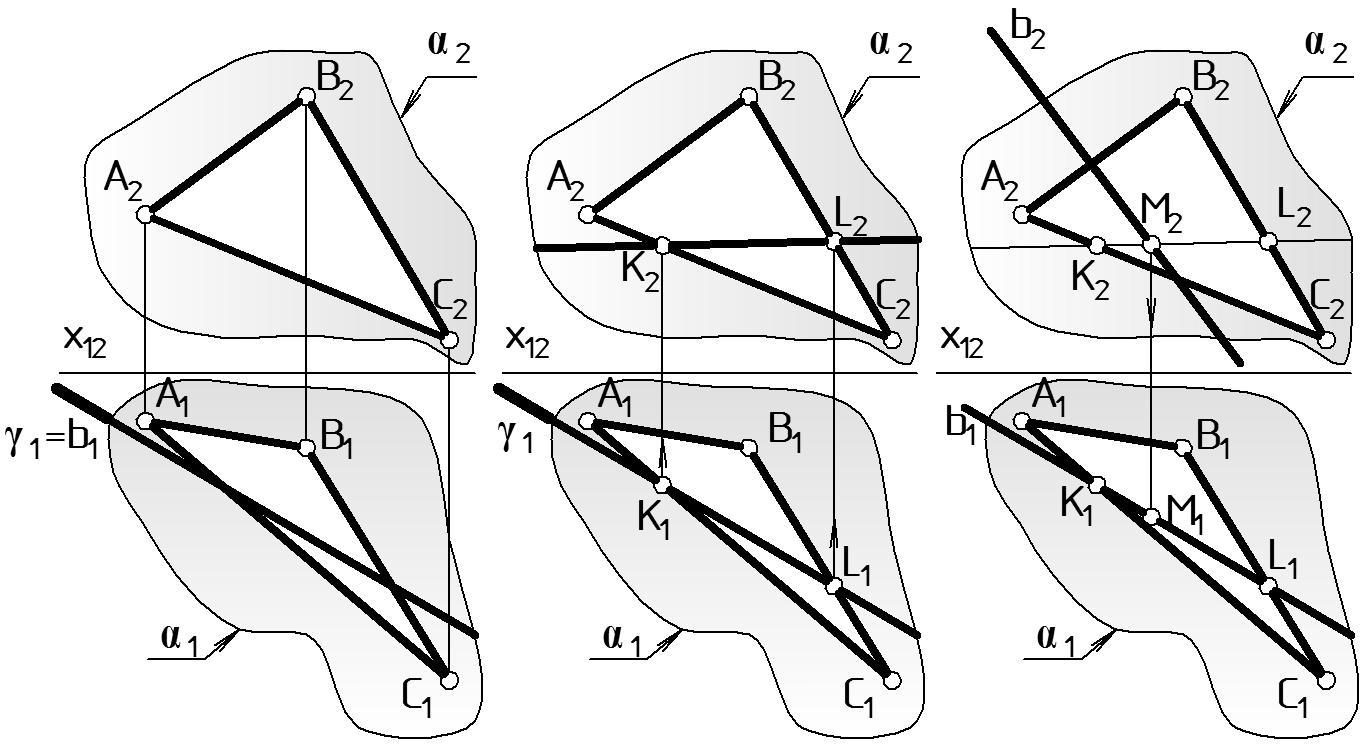
Этап 1. Прямую b общего положения заключают во вспомогательную проецирующую плоскость-посредник. В данном случае (Рис. 34 б) это горизонтально-проецирующая плоскость ( ₁ )  П₁, которая на чертеже задается горизонтальным следом ₁ с указанием собирательного свойства следа отрезком утолщенной линии. След совпадает с проекцией прямой b₁, что отображается равенством ₁ = b₁. Проекция прямой b₂ в этом этапе не участвует, поэтому на чертеже пока не показана.

а б в Рисунок 34

Этап 2. Находится линия пересечения вспомогательной проецирующей плоскости-посредника  с заданной плоскостью : (KL) =    (Рис. 34 б). Проекции прямой b в этом этапе не участвуют, поэтому на чертеже пока не показаны. Ход решения этого этапа соответствует решению Задачи 3, показанной на рис. 32. Горизонтальная проекция (К₁L₁) совпадает с горизонтальным следом плоскости: К₁ = ₁  [ А₁В₁ ]; L₁ = ₁  [ C₁В₁ ]. Фронтальные проекции этих точек строятся по линии связи: К₂  [ А₂В₂ ]; L₂  [ C₂В₂ ]. Проводим через К₂ и L₂ фронтальную проекцию линии пересечения плоскостей.

Этап 3. Находится точка M пересечения заданной прямой b c найденной на втором этапе прямой (KL). Сначала точка отмечается на плоскости П₂: M₂ = (К₂L₂)  b₂, затем по линии связи находится M₁  b₁.

В результате этих трех этапов будет найдена точка M (M₁; M₂) пересечения прямой общего положения b с плоскостью общего положения .

Замечание: при решении задачи можно использовать фронтально-проеци-рующую плоскость ( ₂ )  П₂, решение при этом выполняется аналогично.

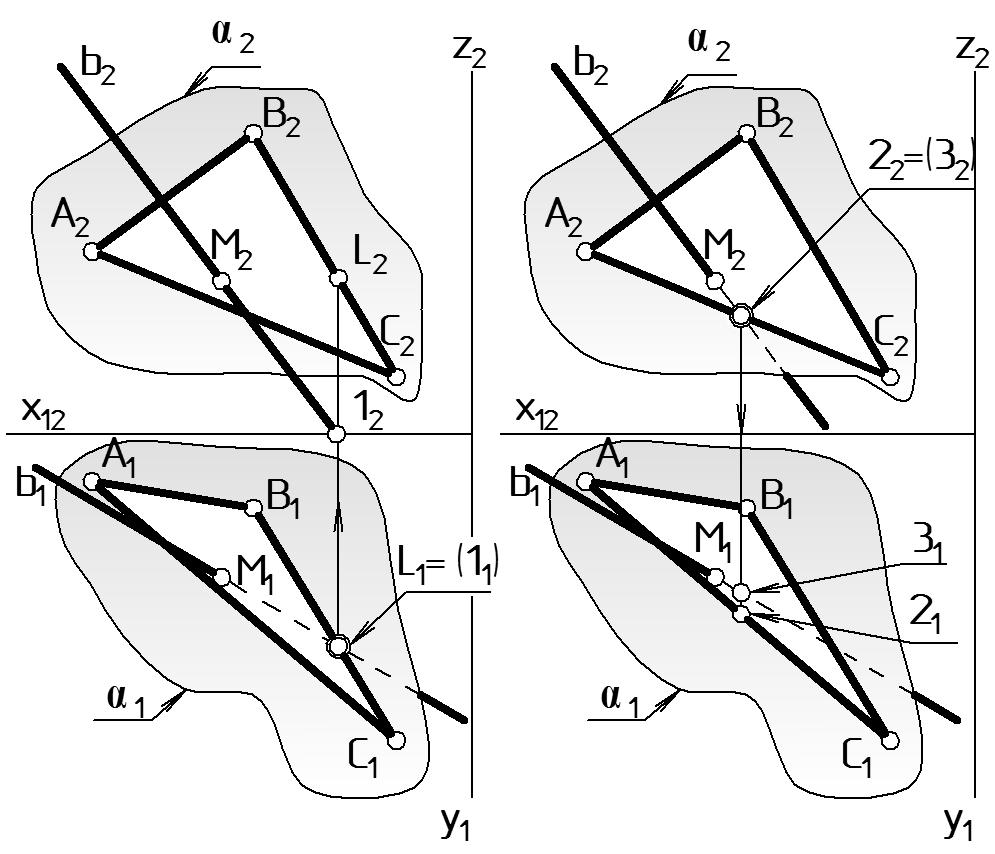
Видимость отрезка прямой линии относительно плоскости устанавливается для каждой плоскости проекций отдельно по методу конкурирующих точек. Покажем, как применяется этот метод на примере рис. 35.

Этап 1. Определим видимость проекции b₁ относительно ₁ на П₁ (Рис. 35 а).

а б Рисунок 35

Для этого в качестве конкурирующих выберем точку L, принадлежащую отрезку СB, а значит плоскости  (АВС), и точку 1, принадлежащую прямой b. Эти точки конкурирующие, так как они лежат на одной фронтально проецирующей прямой, поэтому их горизонтальные проекции совпадают: L₁ = 1₁. Посмотрим на П₂ высота какой точки больше? Для этого сравним координаты z точек L₂ и 1₂. z_L  z₁, то есть высота точки L больше, следовательно, L₁ видима. Отметим скобками, что проекция 1₁, принадлежащая прямой b, закрыта (невидима). Значит, прямая b₁ в этом месте до точки пересечения M₁ будет невидима на П₁, соответственно левее точки M₁ она будет видима.

Этап 2. Теперь определим видимость проекции b₂ относительно ₂ на П₂ (Рис. 35 б)_. Для этого в качестве конкурирующих выберем точку 2, принадлежащую отрезку АС, а значит плоскости  (АВС) , и точку 3, принадлежащую прямой b. Эти точки конкурирующие, так как они лежат на одной горизонтально проецирующей прямой, поэтому их фронтальные проекции совпадают: 2₂ = 3₂. Посмотрим на П₁ глубина какой точки больше? Для этого сравним координаты y точек 2₁ и 3₁. y₂  y₃, то есть глубина точки 2 больше, следовательно, 2₂ видима. Отметим скобками, что проекция 3₂, которая принадлежит прямой b, невидима. Значит, прямая b₂ в этом месте до точки пересечения M₂ будет невидима на П₂, соответственно левее точки M₂ она будет видима.