2 Подготовка данных для исследования динамической устойчивости синхронной машины

2.1 Уравнение движения ротора в относительных единицах

Запишите уравнение (1.23) в следующем виде

Обозначьте:

У

равнение (2.1) примет следующий вид

Уравнение (2.4) является исходным при исследовании влияния демпферной обмотки на качания ротора в переходных режимах.

2.2 Исходные данные

Как и в предыдущих лабораторных работах по исследованию динамической устойчивости синхронной машины студентом исследуются переходные процессы синхронного двигателя, который был спроектирован им при выполнении курсового проекта по курсу «Инженерное проектирование электромеханических устройств – Синхронные машины».

Для исследования влияния демпферной обмотки на качания ротора необходимы данные, приведенные в таблице 2.1:

Момент инерции ротора при проектировании синхронной машины не определялся. Его достаточно точно можно посчитать по следующей формуле.

Момент инерции ротора J, кг-м².

где К - коэффициент приведения момента инерции механизма к валу синхронной машины с учетом массы вала . Примите К=2.

Общую массу ротора определите, как

где | - масса меди обмотки возбуждения, кг;

- масса меди стержней пусковой обмотки, кг;

— масса меди короткозамыкающих колец, кг;

- масса стали полюсов, кг;

- масса стали обода ротора, кг;

Таблица 2.1 - Исходные данные для исследования переходных режимов

Данные курсового проекта						Рассчитываемые величины
кВт		о.е.	о.е.	о.е.	м	кг	кг м2	о.е.	о.е.	о.е.	о.е.
500	6	2,2	1,98	0,2	0,9	1120	454	780	23,8	0,015	0,053

В качестве примера взяты данные синхронного двигателя, рассчитанного в [1].

3 Исследование влияния демпферной обмотки на качания ротора средствами MathCaDa

Для решения дифференциального уравнения (2.4) воспользуйтесь операторным методом решения дифференциальных уравнений. Найдите изображение уравнения по методу Лапласа:

3.1 Операторное уравнение (2.4)

- наберите левую часть уравнения (2.4)

- пометьте курсором переменную t:

- вызовите команду "преобразование Лапласа" меню Symbolics (Символы).

Получите:

-введите начальные условия

Сброс или наброс нагрузки вызывает первоначальное изменение угла нагрузки на величину . Обозначьте в уравнении (3.2) как .

Скорость изменения угла нагрузки в начальный момент переходного режима равна 0

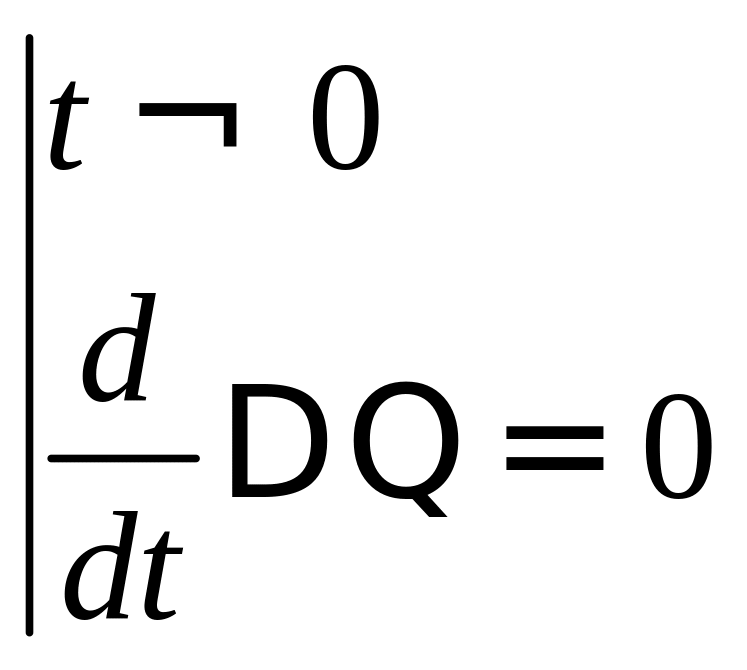
- введите обозначение:

-получите уравнение (3.2) в операторной форме

Обратите внимание на то, что для проведения замен необходимо пользоваться копированием переменных или частей уравнения, а не переписывать их. Это значительно сократить время на преобразование уравнений и позволит избежать ошибок в обозначении величин. Помните, что MathCad различает большие и малые прописные буквы.