ИССЛЕДОВАНИЕ ДИНАМИЧЕСКОЙ УСТОЙЧИВОСТИ СИНХРОННЫХ МАШИН

Лабораторная работа 3

Исследование влияния демпферной обмотки на качания ротора синхронной машины при отсутствии гармонических сил сопротивления

Цель работы: Изучить влияние демпферной обмотки на качания ротора синхронной машины при отсутствии гармонических сил сопротивления; исследовать закон движения ротора синхронной машины с демпферной обмоткой средствами MathCada. Проанализировать влияние демпфирующего момента на качания ротора.

Программа лабораторной работы:

1. Изучить вопросы, связанные с созданием демпфирующего момента и установить его связь с приращением угла нагрузки синхронной машины.

2. Составить математическую модель синхронной машины с демпферной обмоткой при отсутствии гармонических составляющих момента сил сопротивления;

4. Исследовать закон движения ротора синхронной машины с демпферной обмоткой при отсутствии гармонической составляющей момента сил сопротивления;

5. Построить графики изменения утла нагрузки при переходных режимах и исследовать зависимость переходных процессов:

• от величины демпфирующего момента;

• от величины момента инерции ротора.

1 Основные вопросы теории, которые необходимо изучить при подготовке к отработке лабораторной работы,

1.1 Уравнение движения ротора

При исследовании динамической устойчивости синхронной машины угловая скорость вращения ротора является неизвестной и переменной величиной, приводящей к изменению угла нагрузки .

Для получения аналитического решения при исследовании динамической устойчивости синхронной машины можно пренебречь электромагнитными переходными процессами. В этом случае можно рассматривать только механические переходные процессы с учетом статических механических характеристик и уравнение движения ротора будет иметь следующий вид

где - момент инерции ротора, кг м 2;

- угловая скорость вращения ротора, рад/с;

- электромагнитный момент синхронной машины, Нм;

-асинхронный момент, Нм.

Следует помнить, что в электрических машинах различают геометрический угол (геометрический радиан) и электрический угол (электрический радиан), которые связаны между собой зависимостью:

где р - число пар полюсов.

Угловая скорость вращения ротора определяется геометрическим углом, а угол нагрузки выражается электрическими радианами. Для приведения величин к одной системе измерения углов выразим угловую скорость вращения ротора через электрические радианы, получим;

Уравнение движения ротора примет следующий вид

1.2 Динамический момент

Динамический момент возникает в результате изменения угловой скорости вращения ротора:

Выразим угловую скорость вращения ротора через приращение угла нагрузки .

Угол нагрузки (рисунок 1.1) равен,

где - угол, определяющий положение оси магнитного поля машины по отношению к оси фазы А;

- угол, определяющий положение полюсов (оси d) по отношению к оси фазы А (рисунок 1.1 представлен для двигательного режима работы синхронной машины).

Угол нагрузки в переходном режиме можно представить как сумму составляющих

где - угол нагрузки в начальный момент (до переходного режима)

- приращение угла нагрузки в переходном режиме.

Тогда уравнение (1.3) примет следующий вид

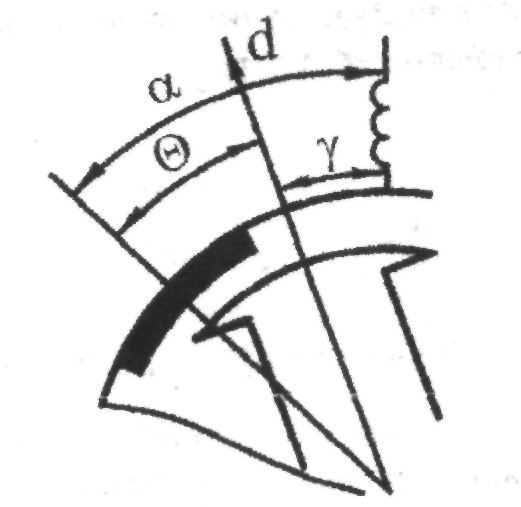
Рисунок 1.1 - К нахождению зависимости угловой скорости вращения ротора от приращения угла нагрузки

Продифференцируем левую и правую часть уравнения (1.5), получим

где - синхронная угловая скорость вращения магнитного поля

машины (при работе машины в режиме двигателя постоянная величина и зависит от частоты сети и числа пар полюсов машины);

- угловая скорость вращения ротора синхронной машины.

Таким образом, угловая скорость вращения ротора связана с приращением угла загрузки следующей зависимостью

Производная по времени от угловой скорости вращения ротора

Подставим (1.8) в (1.2) получим выражение динамического момента в зависимости от приращения угла нагрузки