1.3 Синхронизирующий момент при малых качаниях ротора

Синхронный электромагнитный момент, обусловленный взаимодействием вращающегося поля якоря с главными полюсами, если пренебречь его реактивной составляющей, обусловленной непостоянством воздушного зазора, изменяется по синусоидальному закону в функции угла нагрузки <9 и выражается следующей зависимостью,

где - угол между осью результирующего магнитного поля в воздушном зазоре машины и продольной осью ротора;

- максимальная величина синхронного момента.

При работе двигателя с постоянным моментом сопротивления на валу машина имеет угол нагрузки . При сбросе или набросе нагрузки происходит изменение угла нагрузки: , возникает дополнительный синхронизирующий момент, который при малых изменениях угла нагрузки пропорционален отклонению угла от среднего значения

Из уравнения (1.12) следует, что дополнительный синхронизирующий момент знакопеременный (зависит от знака ), что при наличии инерционности вращающихся масс приводит к возникновению собственных незатухающих колебаний ротора, которые были изучены в лабораторной работе №1.

1.4 Момент сопротивления на валу машины

В общем случае момент сопротивления на валу машины содержит наряду с постоянным моментом сил сопротивления и периодически изменяющиеся составляющие. Периодические составляющие, в общем случае, изменяются с различными частотами:

где - порядковый номер периодической составляющей момента нагрузки.

В лабораторной работе необходимо исследовать влияние гармонической составляющей момента сил сопротивления на качания ротора, исследовать резонанс и определить как изменяется амплитуда вынужденных колебаний от соотношения частот .

Для упрощения математической модели исследования качаний ротора при наличии гармонических составляющих момента сил сопротивления, рассмотрите такие колебания ротора, при которых средний момент сил сопротивления за один оборот остается постоянным и уравновешивается электромагнитным моментом вращения на валу синхронной машины.

В этом случае изменение угла нагрузки будет вызываться гармонической составляющей момента сил сопротивления:

В данной лабораторной работе необходимо исследовать влияние гармонической составляющей момента сил сопротивления (1.14) на угол нагрузки синхронной машины без демпферной обмотки.

1.5 Уравнение движения ротора в относительных единицах

Подставьте зависимости (1.10), (1.12) и (1.14) в уравнение движения ротора (1.2), получите:

Запишите уравнение (1.15) в относительных единицах. Для этого левую и правую часть уравнения разделите на базовый момент

Примите следующие базовые величины (см. лабораторную работу №1)

; ;

где - номинальная мощность, Вт;

- частота сети, Гц.

а) Динамический момент в относительных единицах

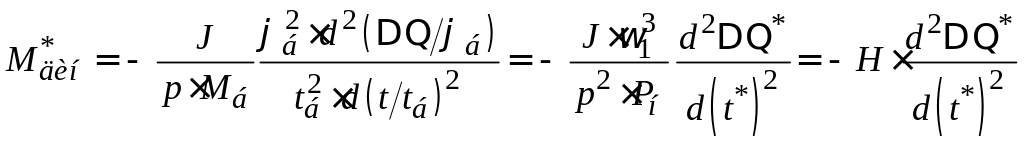
где 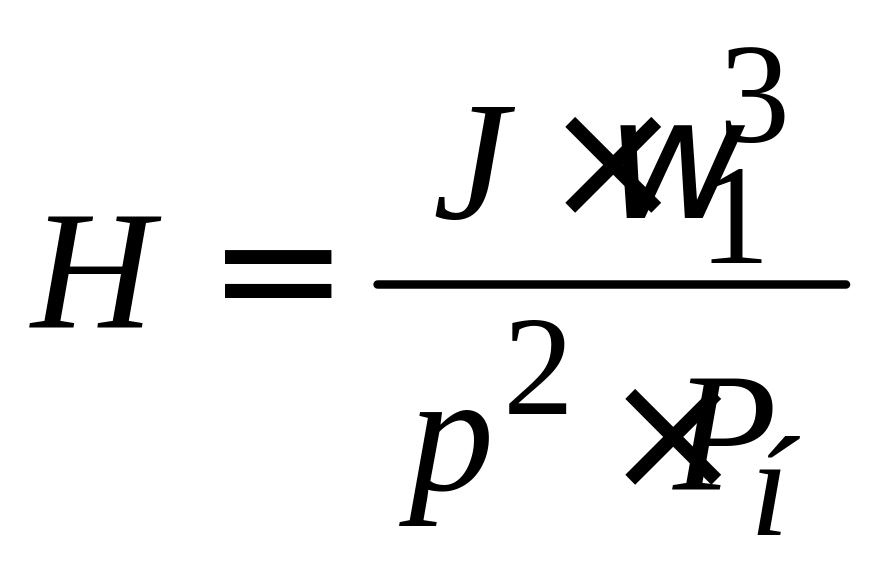- механическая постоянная вращающихся масс

б) Синхронизирующий момент в относительных единицах

где - перегрузочная способность синхронной машины.

г) Гармоническая составляющая момента сил сопротивления в относительных единицах:

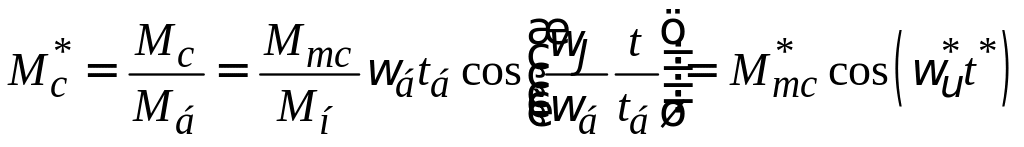
Подставьте полученные значения относительных моментов по формулам (1.18), (1.19) , (1.20) в уравнение (1.16), получите уравнение движения ротора в относительных единицах, которое будет иметь следующий вид:

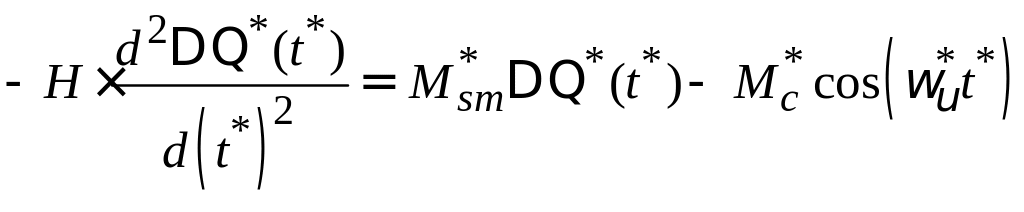
Преобразуйте его к следующему виду

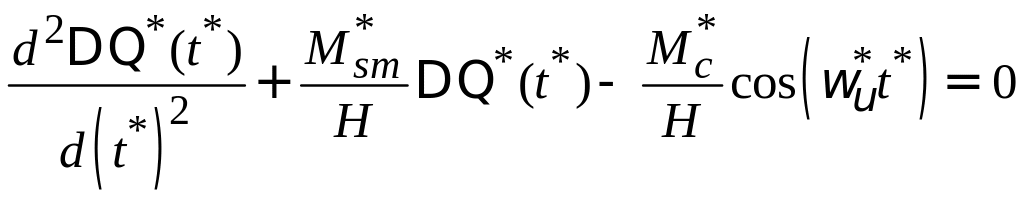
Обозначте - собственная частота колебаний ротора;

где _{- амплитуда гармонической составляющей момента сил сопротивления в относительных единицах}

Окончательно уравнение движения ротора в относительных единицах примет следующий вид:

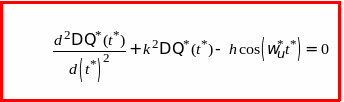
Чтобы при наборе уравнения в MathCADе не загружать его индексами, примените для обозначения абсолютных и относительных величин одни и те же обозначения, а вид величины оговорите особо, как это принято ниже.