3.3 Уравнение движения ротора в относительных единицах

Для получения уравнения движения ртора в относительных единицах подставьте в уравнение (2.4) моменты в относительных единицах согласно (3.9) и(3.13).

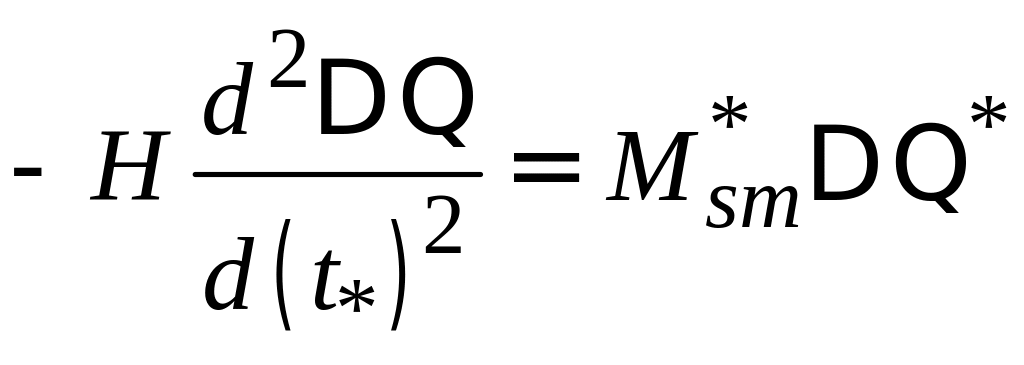
Для решения уравнения (3.14) на ПЭВМ средствами MathCada перепишите его в следующем виде (для того, чтобы не загружать уравнение индексами знак относительной величины опустите):

Обозначьте - частота собственных колебаний ротора (см. (2.5)).

Тогда уравнение для моделирования переходного процесса будет иметь вид

4 Решение уравнения (3.16) средствами MathCada

Для решения дифференциального уравнения второго порядка воспользуйтесь операторным методом решения дифференциальных уравнений. Найдите изображение уравнения по методу Лапласа.

ВНИМАНИЕ! Для проведения замен необходимо пользоваться копированием переменных или частей уравнения, а не переписывать их. Это значительно сократит время на преобразование уравнений и позволит избежать ошибок в обозначении величин. Помните, что MathCad различает большие и малые прописные буквы. Для того, чтобы в идентификаторе переменкой буквы или цифры представить в виде индекса, необходимо перед ними поставить точку. У переменной будет вид индексной переменной, но такой она являться не будет, поэтому имя будет обозначать только одну переменную.

4.1 Получение уравнения (3.16) в операторной форме

- наберите левую часть уравнения (3.16)

• пометьте курсором переменную t;

• вызовите команду "преобразование Лапласа" меню Symbolics (Символы). Получите:

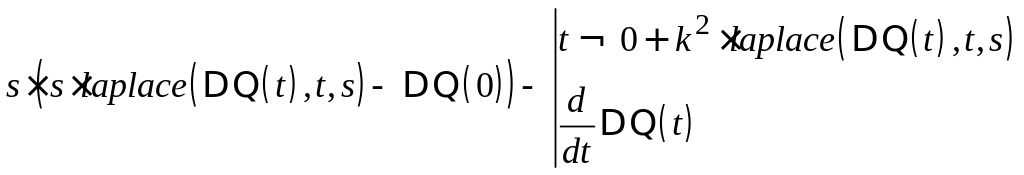
- введите начальные условия;

Сброс или наброс нагрузки вызывает первоначальное изменение угла нагрузки на величину .

Обозначьте в уравнении (4.2) . как .

Скорость изменения угла нагрузки в начальный момент переходного режима равна 0:

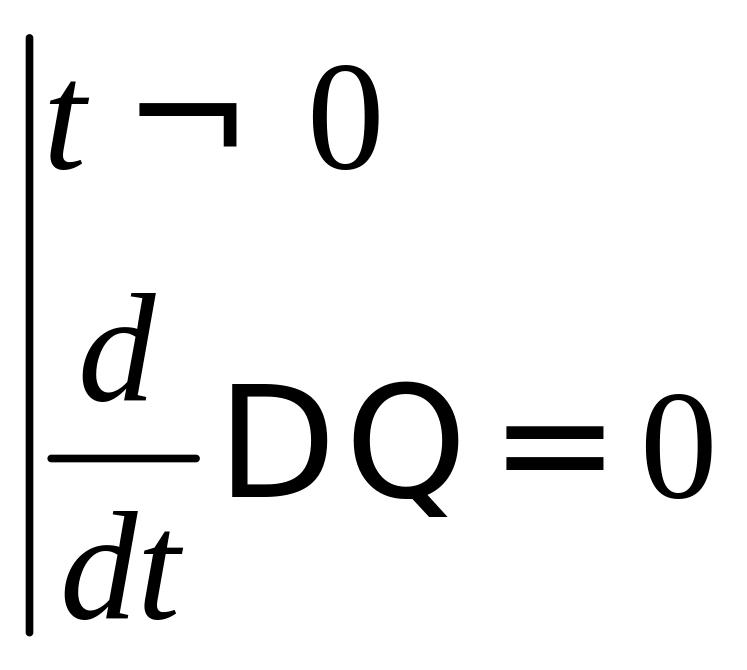
- введите обозначение:

• получите уравнение (3.16) в операторной форме

4.2 Нахождение переменной

Для нахождения переменной воспользуйтесь командой «solve» меню «Символы»

В левый квадрат вставьте путем копирования уравнение (4.3), а в правый – .

Щелкните мышкой за пределами поля формулы, получите;

Если ПЭВМ при вызове команды «solve» предложит Вам следующий вид оператора логического вычисления:

следует в левый квадрат вставить уравнение (4.3), убрать второй квадрат и запятую (Delete или Back Space), поставить запятую после оператора «solve» - появится квадрат после оператора, введите в него переменную.

Для получения закона изменения примените обратное преобразование Лапласа. Для этого пометьте переменную s, в меню «Символы» выберите подменю «Преобразование» и вызовите команду «обратное Лапласа», получите:

Уравнение (4.7) и представляет собой искомый закон изменения угла нагрузки синхронной машины без демпферной обмотки и гармонических сил сопротивления на валу.

где

5 Исследование закона изменения угла нагрузки

Исследование проведите путем построения графиков при изменении параметров, определяющих закон изменения этой величины.

Исходные данные для исследования статической устойчивости синхронного двигателя

Студент исследует переходные процессы синхронного двигателя, который был спроектирован им при выполнении курсового проекта по курсу «Инженерное проектирование электромеханических устройств - Синхронные машины».

Для исследования статической устойчивости двигателя необходимы следующие данные:

-номинальное напряжение В;

• номинальный ток, , А;

• число пар полюсов, р;

-перегрузочная способность двигателя

• коэффициент нагрузки, (задается преподавателем);

• момент инерции ротора _{, кг м}²

Момент инерции вращающихся масс рассчитайте как

где К - коэффициент приведения момента инерции механизма к валу синхронной машины с учетом массы вала (задается преподавателем);

- масса активных материалов ротора;

где - масса меди обмотки возбуждения, кг;

- масса меди стержней пусковой обмотки, кг;

- масса меди короткозамыкающих колец, кг;

- масса стали полюсов, кг;

- масса стали обода ротора, кг;

Пример подготовки данных для построения графика изменения угла нагрузки, приведен в таблице 5.1. В качестве примера взяты данные синхронного двигателя, рассчитанного в [1].

Прежде чем строить графики обязательно задайте численные значения величин, входящих в уравнение (4.6) Помните, что в MathCade утлы измеряются в радианах.

Для построения нескольких графиков в одной системе координатных осей при различных значениях одних и тех же величин обозначьте их различными индексами;

Например:

Таблица 5.1- Исходные данные

Масса, кг.						Число пар полюсов	Перегрузочная способность	Диаметр статора, м	Номинальная мощность, Вт.
					Итого	p		D
181	19	635	254	31	1120	6	2.2	0.9	5000000

Таблица 5.2 - Вычисленные данные

1/c
	кг м2		о.е.		о.е.
314	K=2	K=3	K=2	K=3	K=2	K=3
	454	681	780	1171	0,053	0,043

5.2 К построению графиков

5.2.1 Скопируйте уравнение (4.6) после принятых численных значений.

5.2.2 Переобозначьте на , а на

Эту операцию MathCad может выполнить автоматически. Для этою наберите, например, , запомните его в буфер. Пометьте в уравнении ту величину, которую необходимо заменить. В меню «Символы» выберите подменю «Переменные» и вызовите команду «Замена». MathCad заменит на .

Этой возможностью MathCada особенно рекомендует пользоваться, когда решение содержит много членов, в которые входят величины, подлежащие переобозначению. Аналогично замените на .

Примечание. Для быстрого выделения уравнения, которое будет копироваться в буфер или в котором будет производиться замена переменных, необходимо курсором справа на лево пометить копируемое уравнение.

5.2.3 В меню "Вставка" вызовите команду "График", заполните метки графика путем копирования переменных в соответствующие незаполненные квадраты.

Масштаб переменных можно изменить, вставив по осям пределы изменения независимой и зависимой переменных.

Для вызова панели редактирования рисунка необходимо дважды щелкнуть левой клавишей при нахождении курсора в площади рисунка. Для редактирования осей - щелкните дважды на соответствующей оси. При наличии цветного принтера выполните графики различными цветами.

При построении графиков с целью проведения анализа влияния различных величин на закон изменения угла нагрузки, не допускайте, чтобы в одной системе координатных осей приводились графики, у которых изменяются одновременно несколько величин, что затрудняет анализ влияния величин на закон изменения угла нагрузки.

Рассмотрим влияние частоты на характер изменения угла нагрузки:

Рисунок 5.1 - Закон изменения угла нагрузки при различных значениях собственной частоты колебаний k.