3 Моменты синхронной машины без демпферной обмотки, возникающие при качаниях ротора с малой, амплитудой

3.1 Динамический момент

Динамический момент возникает в результате изменения угловой скорости вращения ротора.

Изменение угловой скорости вращения ротора синхронного двигателя вызывает изменение угла нагрузки, что и необходимо исследовать в лабораторной работе.

Выразите угловую скорость вращения ротора ш через приращение угла нагрузки Л(9 исходя из следующего.

Угол нагрузки Θ (рисунок 1.1) равен,

где - угол, определяющий положение оси магнитного поля машины по отношению к оси фазы А;

- угол, определяющий положение полюсов (оси d) по отношению к оси фазы А (рисунок 3.1 представлен для двигательного режима работы синхронной машины).

Угол нагрузки в переходном режиме можно представить как сумму составляющих

где - угол нагрузки в начальный момент (до переходного режима), зависящий от величины момента сопротивления на валу;

- приращение уїла нагрузки в переходном режиме, которое возникает под действием возмущения.

Тогда уравнение (3.2) примет следующий вид

Рисунок 3.1 К нахождению зависимости угловой скорости вращения ротора от приращения угла нагрузки

Продифференцируйте левую и правую часть уравнения (3.4), получите

где - синхронная угловая скорость вращения магнитного поля машины (при работе машины в режиме двигателя постоянная величина, которая зависит от частоты сети и числа пар полюсов машины);

- угловая скорость вращения ротора синхронной машины.

Таким образом, угловая скорость вращения ротора связана с приращением утла нагрузки А& следующей зависимостью

Возьмите производную по времени от угловой скорости вращения ротора

Подставьте (3.7) в (3.1), получите выражение динамического момента в зависимости от приращения угла нагрузки

Найдите выражение динамический момент в относительных единицах. Для этого разделите динамический момент на базовое значение момента, которое равно номинальному (см. табл. 1.1).

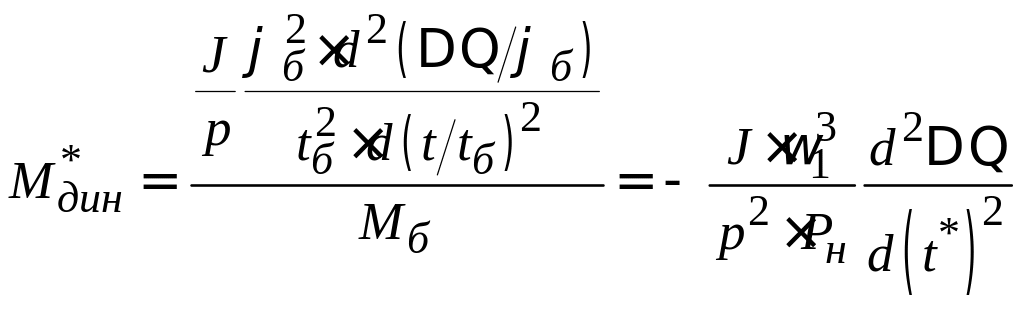
Обозначьте и получите

где H - механическая постоянная вращающихся масс

3.2 Синхронизирующий момент

У синхронной машины без демпферной обмотки электромагнитный момент равен синхронному моменту, т.е.

Синхронный электромагнитный момент, возникающий при взаимодействии вращающегося поля якоря с главными полюсами, если пренебречь его реактивной составляющей, обусловленной непостоянством воздушного зазора, изменяется по синусоидальному закону в функции угла нагрузки и выражается следующей зависимостью,

где - угол между осью результирующего магнитного поля в воздушном зазоре машины и продольной осью ротора;

- максимальное значение синхронного момента.

При постоянной нагрузке на валу машина работает в установившемся режиме и угол нагрузки является неизменным и уравновешивается моментом сопротивления на валу - моментом нагрузки:

При сбросе или набросе нагрузки, когда происходит изменение угла нагрузки возникает дополнительный синхронизирующий момент, который при малых изменениях угла нагрузки пропорционален отклонению угла от среднего значения .

Синхронизирующий момент в относительных единицах

где