Показники надійності електронних пристроїв

Всі кількісні характеристики надійності мають імовірнісний характер, тому що відмови є випадковими подіями. Визначення імовірнісних (теоретичних) характеристик є складним завданням, тому навіть для простих виробів (наприклад, радіодеталей) звичайно визначають статичні (експериментальні) характеристики надійності. Статичні характеристики знаходять за допомогою математичної обробки результатів великої кількості спостережень, отриманих при експлуатації й випробуванні. При оцінці надійності нового виробу використовують характеристики надійності окремих елементів, які відомі за результатами попередніх випробувань.

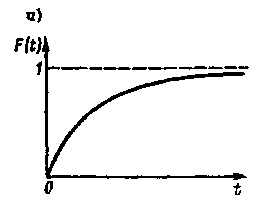
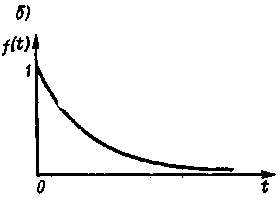
Рис. 8.1. Графік функції розподілу випадкової величини:

a - інтегральний закон F(t);

б - диференціальний закон f(t)

Показники надійності можуть бути одиничними або комплексними. Одиничний показник характеризує одну із властивостей надійності об'єкта, комплексний показник - кілька властивостей, що складають надійність об'єкта.

Електронна апаратура відноситься до класу неремонтованої. Показниками надійності неремонтованих виробів є, імовірність безвідмовної роботи, середнє напрацювання до відмови й інтенсивність відмов.

Імовірністю безвідмовної роботи P(t₀) називають імовірність того, що в межах заданого напрацювання відмови в об'єкті не виникне. В інтервалі від 0 до t₀ імовірність безвідмовної роботи визначають по формулі:

P(t_o)=1-F(t_o), (8.1)

імовірність відмови Q(t_o) - по формулі

Q(t_o) =F(t_o)=1-P(t_o), (8.2)

де F(t_o), - функція розподілу напрацювання до відмови.

Функцію F(t) називають інтегральним законом розподілу випадкової величини t. Значення функції розподілу перебувають в інтервалі . Графік функції розподілу показаний на мал. 8.1 а.

Похідну від функції розподілу F(t) називають диференціальним законом розподілу f(t), а графік щільності ймовірності f(t) - кривою розподілу.

Функцію розподілу можна виразити через щільність імовірності:

(8.3)

У теорії надійності використовують експонентний закон розподілу безперервної випадкової величини, для якого з розподілу (мал. 8.1, б)

(8.4)

де , - інтенсивність відмов.

Експонентний закон розподілу можна розглядати як окремий випадок розподілу Вейбулла.

Основними характеристиками експонентного закону розподіли є математичне очікування М(t)=1/ і дисперсія . Після перетворення формули (8.3) одержимо

(8.5)

Підставляючи значення F(t) в (8.1), одержимо

(8.6)

Рівняння (8.6) називають експонентним законом надійності, з якого виходить, що надійність об'єкта убуває із часом по експонентній кривій. Це рівняння використовують звичайно при оцінці надійності складних систем, відмови яких обумовлені більшою кількістю вхідних у них комплектуючих елементів. Великою перевагою експонентного закону є його простота.

Середнє напрацювання до відмови визначається як очікуваний час справної роботи до першої відмови:

(8.7)

Де - середнє напрацювання до відмови.

Інтенсивність відмов представляє умовну щільність імовірності виникнення відмов у системі в деякий момент часу напрацювання за умови, що до цього моменту відмов у системі не було. Величина визначається відношенням

(8.8)

Інтенсивність відмов називають -характеристикою. Приблизно неї визначають по формулі

(8.9)

де n(t) - число систем (елементів), що відмовили протягом розглянутого проміжку часу ; N(t) - кількість систем (елементів), роботоздатних до початку проміжку часу

Величина показує, яка частина елементів відносно середнього числа справно працюючих елементів виходить із ладу в одиницю часу (звичайно в 1 год).

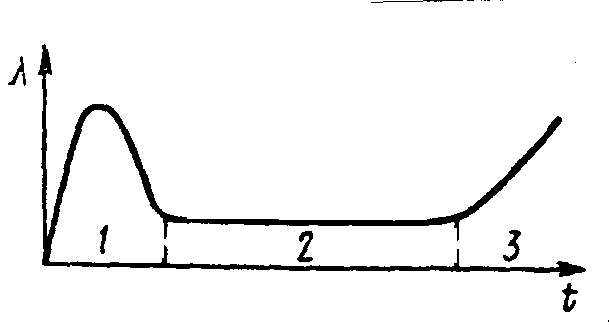
Рис 8.2. Типова крива інтенсивності відмов

Типова крива інтенсивності відмов (мал. 8.2) може бути розділена на три ділянки

Ділянка 1, що відповідає етапу напрацювання, характеризується підвищеною інтенсивністю раптових відмов, що є наслідком неякісного виготовлення. Бажано, щоб цей етап закінчувався на заводі-виготовлювачі.

Ділянка 2, що відповідає етапу нормальної роботи, характеризується нормальним строком експлуатації виробу. Інтенсивність відмов зменшується, тому що етап напрацювання закінчився, а зношування деталей (елементів) ще не наступив. Імовірність нормальної роботи елементів на цьому етапі визначається законом Пуассона (законом рідких явищ).

Ділянка 3 характеризується новим наростанням інтенсивності відмов, що є результатом старіння або зношування елементів. На етапі нормальної роботи між інтенсивністю відмов і середнім часом t_cp справної роботи є залежність

(8.10)

Показниками надійності ремонтованих виробів є

• коефіцієнт готовності,

• напрацювання на відмову,

• параметр потоку відмов,

• імовірність безвідмовної роботи,

• середній час відновлення й ін.

Коефіцієнт готовності К_Г являє приклад комплексного показника, тому що він характеризує два складові показники надійності: напрацювання на відмову Т_о і середній час відновлення Т_В тобто

К_Г=Т₀/(Т₀+Т_В) (8.11)