Контрольные вопросы

1.  Что такое живое сечение потока, смоченный периметр и гидравлический радиус?

2.  Что называют расходом и средней скоростью потока жидкости?

3.  Сформулируйте и запишите уравнение неразрывности для потока жидкости?

4. Дайте определение понятий расхода и средней скорости.

5.  Что называют полной удельной энергией потока в произвольном сечении?

6. Запишите уравнение Бернулли для потока реальной жидкости?

7. В чем состоит геометрический смысл уравнения Бернулли?

8. В чем состоит энергетический смысл уравнения Бернулли?

9. Дайте определение понятия полного напора.

10. Что такое гидравлический уклон?

11. Почему напорная линия всегда нисходящая?

12.  На каком расстоянии друг от друга располагаются напорная и пьезометрическая линии?

13. Могут ли напорная и пьезометрическая линии пересекаться?

14.  В каком случае пьезометрическая линия может проходить ниже оси трубопровода?

15.  Как изменится расстояние между напорной и пьезометрическими линиями при увеличении расхода жидкости в трубопроводе?

16.  Как изменяется площадь живого сечения вдоль потока, если расстояние между напорной и пьезометрическими линиями вдоль потока при протекании по трубопроводу жидкости с постоянным расходом увеличится?

17.  Чем вызывается неравномерность распределения скоростей по сечению потока и как она учитывается в уравнении Бернулли?

18. От чего зависит коэффициент гидравлического трения ?

19. Какие трубы называются гидравлически гладкими?

20. Что называется местным сопротивлением?

21. Чем обусловлена потеря напора в местных сопротивлениях?

22.  По какой формуле находятся потери напора в местных сопротивлениях?

3. Равномерное безнапорное установившееся движение воды в каналах

Равномерным называется такое движение, когда площадь живого сечения , средняя скорость v, а также эпюра распределения скорости по живому сечению не меняются вдоль потока.

П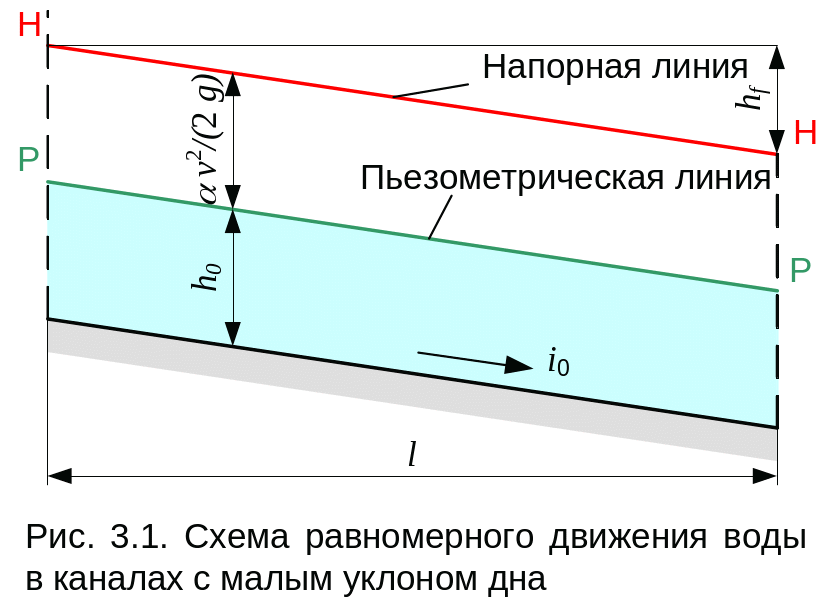 ри этом движении глубина потока по его длине не меняется и называется нормальной глубиной h₀.

При равномерном движении напорная линия Н–Н, линия свободной поверхности, она же пьезометрическая линия Р–Р, и линия дна канала параллельны (рис. 3.1). Следовательно, гидравлический уклон равен пьезометрическому и равен уклону дна канала i₀.

Так как величина уклона обычно невелика, считают, что поперечные сечения вертикальны.

Основные зависимости, используемые при расчете равномерного безнапорного движения воды в каналах,

; (3.1)

. (3.2)

П оперечное сечение каналов может иметь различные формы (рис. 3.2), однако наибольшее распространение получили каналы трапецеидального сечения. Здесь: b – ширина канала по дну, м; h – глубина воды, м; m – коэффициент откоса, равный ctg; B – ширина потока поверху, м;  – площадь живого сечения, м²;  – смоченный периметр, м.

Формулы для определения  и.

1. Трапецеидальное сечение:

; (3.3)

; (3.4)

. (3.5)

2. Прямоугольное сечение, :

; (3.6)

. (3.7)

3. Треугольное сечение, :

; (3.8)

. (3.9)

4. Круглое сечение:

(3.10)

(3.11)

; (3.12)

(3.13)

Гидравлический радиус находится по формуле

. (3.14)

Коэффициент Шези в (3.2) определяется по формуле Павловского

, (3.15)

где n – коэффициент шероховатости, принимаемый по табл. 3.1; y – показатель степени.

. (3.16)

Таблица 3.1