2.2.2. Основная расчетная формула для прямоугольного водослива

Расход через водослив определяется по формуле:

, (2.1)

где – скорость на гребне водослива; – площадь струи на гребне водослива.

Так как площадь прямо пропорциональна произведению b H, а скорость величине , то расход можно переписать как

, или , (2.2)

где – коэффициент пропорциональности.

Влияние скорости подхода на величину расхода учитывается величиной полного напора . Следовательно, расчетная формула для определения расхода будет

. (2.3)

Безразмерный коэффициент называется коэффициентом расхода водослива.

2.2.3. Неподтопленный водослив с тонкой стенкой

Водослив при отсутствии бокового сжатия, когда под струей имеется атмосферное давление, называется нормальным. Величина расхода для такого водослива определяется по формуле:

. (2.4)

Здесь скорость подхода учитывается коэффициентом расхода .

Существует несколько различных эмпирических формул для определения коэффициента расхода , наиболее используемая

. (2.5)

Ее можно применять, когда и м.

2.2.4. Подтопленный водослив с тонкой стенкой

Подтопленный водослив с тонкой стенкой получается при соблюдении следующих условий:

1) горизонт воды нижнего бьефа располагается выше гребня водослива , где – высота подтопления водослива, то есть превышение горизонта воды нижнего бьефа над гребнем водослива;

2) в нижнем бьефе имеет место спокойный режим движения воды.

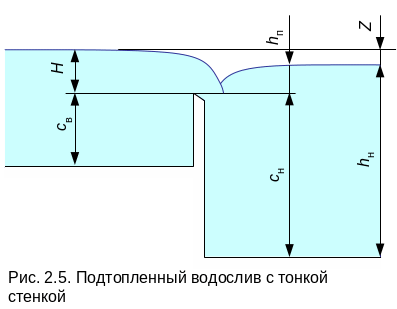
Рис. 2.5. Подтопленный водослив с тонкой стенкой

Если в нижнем бьефе имеет место бурный режим, то за водосливом появляется отогнанный прыжок и водослив оказывается неподтопленным даже если соблюдается условие .

Когда русло нижнего бьефа прямоугольное и , то спокойный режим в нижнем бьефе будет при условии, если так называемый относительный перепад менее 0,7 ¸ 0,75.

Расход для подтопленного прямоугольного водослива без бокового сжатия определяется по формуле:

. (2.7)

Рис. 2.6. Неподтопленный водослив

Величина согласно Базену находится по эмпирической формуле:

. (2.8)

2.3. Описание установки

Схема экспериментальной установки, изображенная на рис. 1.4, представляет собой прямоугольный лоток с прозрачными стенками, в котором установлен водослив см. рис. 2.7.

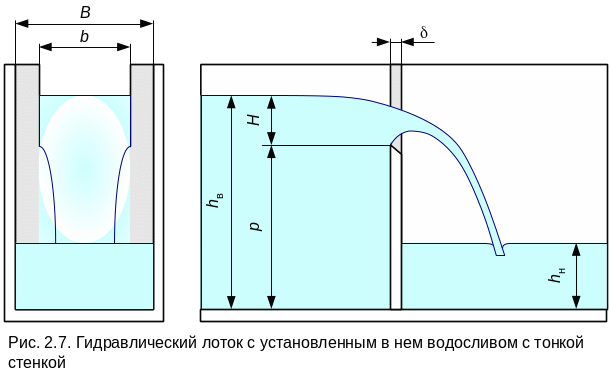
Рис. 2.7. Гидравлический лоток с установленным в нем водосливом с тонкой стенкой

2.4. Выполнение работы

1. Запустить насос 9 cм. рис. 1.4

2. Задвижкой 11 установить расход Q.

3. Измерить напор на водосливе на расстоянии не менее 5 H перед водосливом.

4. Измерить бытовую глубину.

5. Изменить бытовую глубину с помощью жалюзей и повторить пункты 3 и 4.

6. Опыт повторить четыре раза.

2.5. Обработка результатов

1. Определить полный напор на водосливе

(2.9)

2. Найти критическую глубину

(2.10)

3. Вычислить значение экспериментального коэффициента расхода водослива

(2.11)

где b – ширина порога водослива, см.

4. Определить величину коэффициента расхода по формуле

. (2.12)

5. Найти отношение критической глубины к глубине в нижнем бьефе.

6. Результаты вычислений занести в табл. 2.1.

7. Построить графики коэффициентов расхода:

   1. От напора на водосливе H₀, для неподтопленного водослива;

   2. От отношения критической глубины к глубине в нижнем бьефе. Установить значение отношения критической глубины к глубине в нижнем бьефе, при котором водослив считается подтопленным.

Таблица 2.1