Лабораторная работа № 7 исследования местных потерь напора

7.1. Цель работы

Экспериментально определить коэффициенты местных сопротивлений.

7.2. Теоретические сведения

Местные потери напора – это потери, обусловленные местными гидравлическими сопротивлениями, т. е. такими элементами трубопроводов, в которых вследствие изменения поперечных размеров или конфигурации происходит деформация потока.

Всякая перестройка структуры потока связана с появлением дополнительных касательных напряжений, причиной которых являются возникающие в потоке дополнительные вихреобразования.

Местные потери энергии имеют ту же физическую природу, что и потери по длине, это результат преобразования части механической энергии в тепловую за счет преодоления касательных напряжений трения.

Основные виды местных потерь напора можно условно подразделить на ряд групп, соответствующих определенным видам местных сопротивлений:

 потери, связанные с изменением поперечного сечения потока (внезапное или плавное расширение и сужение);

 потери, вызванные изменением направления потока (колена, угольники, отводы);

 потери, связанные с протеканием жидкости через арматуру различного типа (краны, вентили, задвижки, заслонки, приемные и обратные клапаны, сетки, фильтры);

 потери, связанные с разделением и слиянием потоков (тройники, крестовины).

Общим для всех видов местных сопротивлений является:

 искривление линий тока;

 изменение площади живого сечения;

 отрыв основной струи от стенок с образованием водоворотных зон;

 повышение пульсации скорости и давления.

Местные потери напора определяются по формуле Вейсбаха

, (7.1)

где  – коэффициент местного сопротивления.

Коэффициент местного сопротивления зависит в основном от формы местного сопротивления и его геометрических размеров.

Теоретически достаточно точно коэффициент местного сопротивления при турбулентном режиме движения можно определить для внезапного расширения, когда труба диаметром d₁ переходит в трубу с большим диаметром d₂ (d₂ > d₁). Струя, выходящая из первой трубы, на некоторой длине расширяется и в сечении 2–2 заполняет все поперечное сечение второй трубы (рис. 7.1).

Рис. 7.1. Внезапное расширение струи

Расширение струи сопровождается отрывом ее от стенок и образованием водоворотной зоны, имеющей кольцевую форму. В водоворотной зоне образуются вихри, происходит непрерывный обмен частицами жидкости между основным потоком и завихренной его частью. Основной вихрь порождает другие, более мелкие вихри, что и является причиной потерь энергии, т. е. местных потерь напора h_в.р. Обозначим давление, скорость и площадь потока в сечении 1–1 через p₁, v₁, ₁, а в сечении 2–2 – через p₂, v₂, ₂ (рис. 7.1). Будем считать, что распределение скоростей в сечениях 1–1 и 2–2 равномерное, т. е. ₁ = ₂ = 1, касательное напряжение на стенке трубы между сечениями равно нулю, давление p₁ в сечении 1–1 действует по всей площади ₂.

Запишем для данных сечений уравнение Бернулли с учетом, что z₁ = = z₂ = 0:

. (7.2)

Тогда

. (7.3)

Согласно закону, изменение количества движения отсека жидкости между сечениями 1–1 и 2–2 равно импульсу сил, действующих на этот отсек. Проекция на ось X изменения количества движения определяется по формуле

. (7.4)

Исходя из ранее принятого допущения, на рассматриваемый отсек жидкости действуют только силы гидродинамического давления, проектируемые на ось X,

. (7.5)

Приравнивая выражения (7.4) и (7.5), получаем

. (7.6)

Разделим левую и правую часть уравнения (7.6) на и, учитывая, что , преобразуем его:

. (7.7)

Умножив и разделив правую часть уравнения (7.7) на 2, подставим ее в уравнение (7.3):

. (7.8)

После преобразования окончательно имеем

. (7.9)

Формула (7.9) называется формулой Борда¹. Согласно ей потери напора при внезапном расширении равны скоростному напору потерянной скорости, так как разность (v₁ – v₂) называют потерянной скоростью.

Выражение (7.9) можно привести к другому виду. Выразим первую скорость через вторую, используя уравнение расхода:

. (7.10)

Тогда . (7.11)

Обозначив , (7.12)

где _в.р – коэффициент гидравлического сопротивления при внезапном расширении потока, окончательно получим

. (7.13)

Формула (7.9) может быть преобразована в отличную от (7.11) зависимость, если выразить вторую скорость через первую:

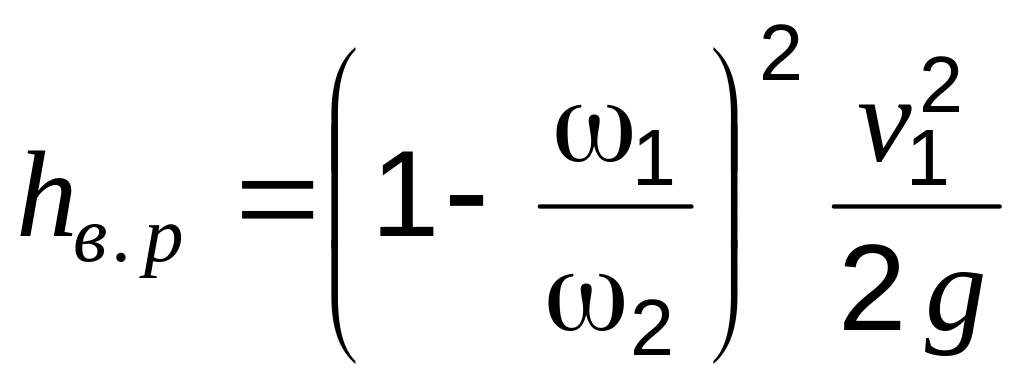. (7.14)

Обозначив 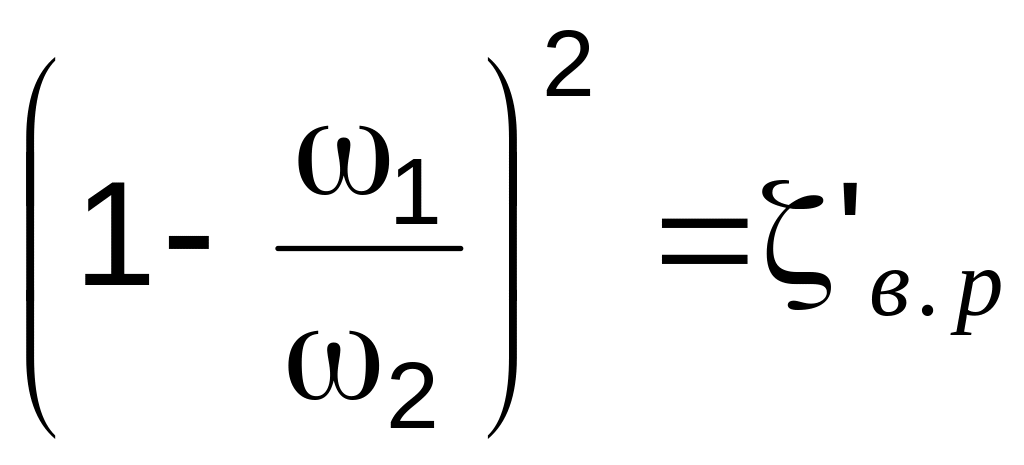, (7.15)

окончательно получим . (7.16)

Р

Рис. 7.2. Внезапное сжатие потока

ассмотрим внезапное сужение, т. е. переход трубы диаметром d₁ в трубу меньшего диаметра d₂ (рис. 7.2).

При переходе из трубы бо́льшего диаметра происходит сжатие потока до _сж, а затем наступает его расширение до ₂. Многочисленные исследования показали, что потери напора на участке сжатия (от ₁ до _сж) пренебрежимо малы по сравнению с потерями напора на участке расширения (от _сж до ₂). Поэтому потери напора при входном сужении могут быть найдены по формуле Борда

. (7.17)

Из уравнения неразрывности потока определим

. (7.18)

Используя понятие коэффициента сжатия струи , преобразуем выражение (7.17):

. (7.19)