12.3. Силы в зацеплении

В зубчатой передаче (рис. 12.8) наклонную силу , расположенную к перпендикуляру к межосевой линии под углом зацепления , расклады-вают по двум направлениям, получая окружное усилие , направленное по касательной к начальной окружности, и радиальное усилие , направлен-ное по радиусу к центру вращения. Такое разложение удобно при расчёте валов и опор.

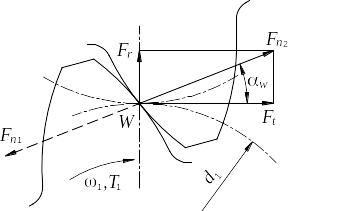
Рис. 12.8. Силы в зацеплении прямозубой передачи

Окружную силу для любой детали вращательного движения определяют по формуле:

либо . (12.2)

Окружная сила на шестерне направлена против направления вращения, на колесе — по направлению вращения.

Радиальное усилие (направлено по радиусу колеса к оси вращения):

. (12.3)

Полная нормальная сила:

. (12.4)

По принципу равенства действия и противодействия силы на колесе противоположны силам на шестерне.

12.4. Расчёты на прочность

Расчёты на прочность цилиндрических зубчатых передач стандартизи-рованы по ГОСТ 21345. Задача расчёта состоит в определении таких зна-чений основных параметров передачи, которые наилучшим образом удов-летворяют прочностным, триботехническим, кинематическим, геометри-ческим и экономическим требованиям.

Исследованиями установлено, что наименьшей контактной усталостной прочностью обладает околополюсная зона рабочей поверхности зубьев. Поэтому расчёт контактных напряжений принято выполнять при контакте в полюсе зацепления (рис. 12.9).

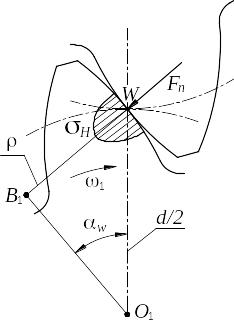
Рис. 12.9. Контактные напряжения в зацеплении

Контакт зубьев можно рассматривать как контакт двух цилиндров с радиусами и . При этом контактные напряжения определяют по соотношениям из теории упругости по формуле Герца:

, (12.8)

где q – удельная нагрузка в Н/мм.

Удельную нагрузку определяют по формуле:

q = F_n/l_Σ, (12.9)

где l_Σ – суммарная длина контактных линий, мм; μ – коэффициент Пуассона; μ = 0,25…0,35; Е – приведенный модуль упругости в МПа;

, (12.10)

где Е₁ и Е₂ – модули упругости соприкасающихся тел; ρ – приведенный радиус кривизны:

; (12.11)

где ρ₁ и ρ₂ – радиусы кривизны контактирующих поверхностей.

Формулу (12.8) значительно упрощают, приняв стальные колёса с 2,1510⁵ МПа и μ = 0,3, а параметры и записать с учётом геометрических соотношений:

; , откуда , (12.12)

. (12.13)

После упрощений формула проверочного расчёта примет вид:

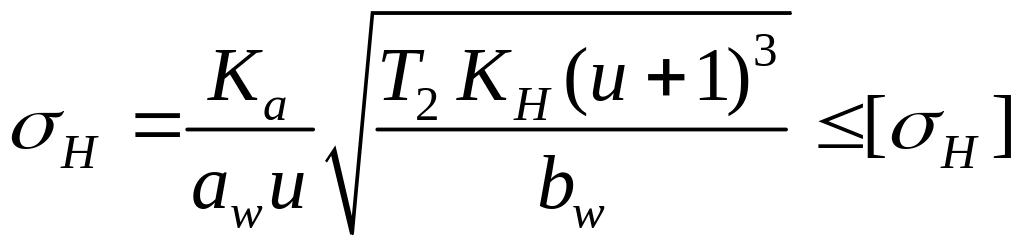. (12.14)

Формула (12.14) непригодна для проектного расчета, так как содержит два неизвестных геометрических параметра – межосевое расстояние и ширину колеса b. Для дальнейшего упрощения решения задачи один параметр выражают через другой. Вводят коэффициент ширины колеса

, откуда . (12.15)

Подставляя (12.15) в формулу (12.14) и решая её относительно , получают формулу проектного расчёта:

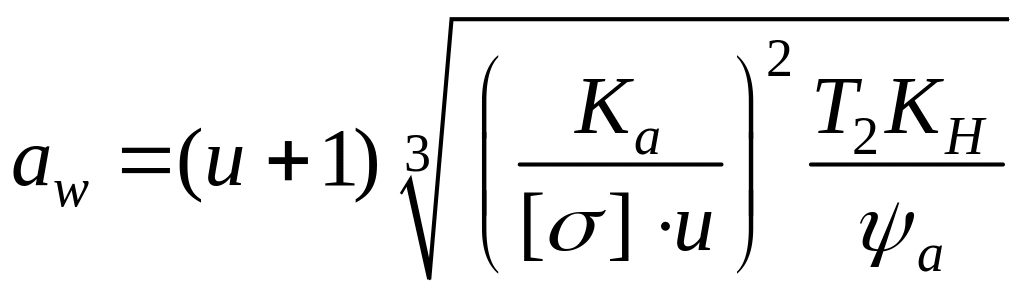, (12.16)

где u – передаточное число (в редукторах равно передаточному отношению); K_a - численный коэффициент, равный 315 для прямозубых колёс; [σ]_H – допу-скаемое контактное напряжение, МПа; Т₂ – вращающий момент на валу коле-са, Н·мм; K_Н – коэффициент нагрузки.

Вычисленное значение в мм округляют до ближайшего значения либо по ГОСТ 2185, либо из ряда R_a40 ГОСТ 6636 (прил. Г). Остальные геометрические параметры определяют в результате расчёта геометрии.

Расчётная схема расчёта зуба на изгиб представлена на рис. 12.10. Зуб рассматривают как консольную балку, нагруженную нормальной силой , которая приложена к кромке зуба (наиболее неблагоприятный случай).

Нормальную силу переносят на ось симметрии зуба и раскладывают на две составляющие: силу , направленную по оси симметрии, и ей перпендикулярную силу . Составляющие силы приводят к опасному сечению с размерами b и s, расположенному вблизи основания зуба. При приведении силы добавляется момент , который будет изгибающим для опасного сечения зуба. Сила является сжимающей.

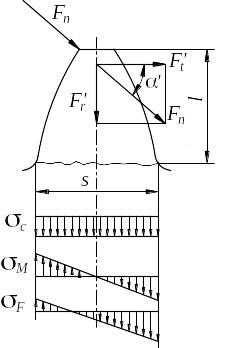
Рис. 12.10. Напряжения на ножке зуба

Напряжения сжатия в опасном сечении:

(12.17)

Напряжения изгиба:

(12.18)

На рис. 13,10 показаны эпюры напряжений, построенные в соответствии с формулами (12.17) и (12.18). Наибольшие суммарные напряжения будут на сжатом (правом) волокне, однако расчёт ведут по растянутому волокну, где наиболее вероятно зарождение усталостных трещин. Результирующее напряжение с учётом концентрации напряжений и коэффициента нагрузки:

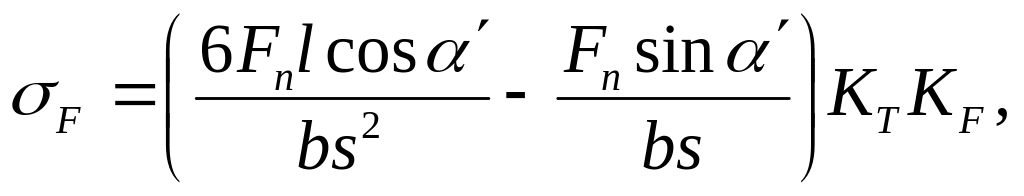(12.19)

где K_T – теоретический коэффициент концентрации напряжений, определяемый методом теории упругости для переходной окружности от эвольвенты к окружности впадин; K_F – коэффициент нагрузки,

С учётом преобразований формула (12.19) примет вид:

, (12.20)

где – коэффициент формы зуба, который зависит от числа зубьев колеса; b_w – рабочая ширина зубьев, мм; m – модуль зацепления, мм.

По формуле (12.20) ведётся проверочный расчёт.