§7. Числовые характеристики непрерывной случайной величины

Пусть случайная величина Х задана своей дифференциальной функцией ƒ(х), причём все её возможные значения принадлежат интервалу .

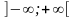Определение 1. Под математическим ожиданием непрерывной случайной величины Х понимается число

Конечно, это определение имеет смысл лишь для такой случайной величины Х, для которой указанный интеграл сходится. Для дисперсии непрерывной случайной величины Х сохраним прежнее определение.

Определение 2.

D(Х) = М[X-(X)]².

Можно доказать (а можно взять в качестве определения), что

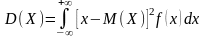
(конечно, в предположении, что интеграл сходится).

Определение 3. Средним квадратическим отклонением непрерывной случайной величины Х называется число

б(Х)=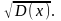

Если все возможные значения непрерывной случайной величины принадлежат интервалу [ а; в ],то

Свойства М(Х), Д(Х) непрерывных случайных величин аналогичны тем, которые имели место для дискретных случайных величин.