Случайные величины

Определение 1. Случайной величиной называют величину, которая в результате испытания принимает одно и только одно из своих возможных значений, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены. Можно дать другое определение.

Определение 2. Случайной величиной называют такую переменную величину, которая принимает значения, зависящие от случая, и при этом можно определить вероятности этих значений.

Примеры:

Различают два типа случайных величин: дискретные и непрерывные.

Определение. Дискретной называют случайную величину, которая может принимать отдельные, изолированные значения с определенными вероятностями.

Примеры:

а) число отказавших элементов в приборе, состоящем из пяти элементов;

б) число самолётов, сбитых в воздушном бою;

Определение. Непрерывной называют случайную величину, которая может принимать любое значение из некоторого конечного или бесконечного промежутка.

§1. Закон распределения дискретной случайной величины

Определение: Законом распределения дискретной случайной величины называют соответствие между всеми возможными её значениями и их вероятностями.

Закон распределения может быть задан:

а) аналитически (в виде функции);

б) таблично. В первой стоке содержатся все возможные значения случайной величины, а во второй - соответствующие вероятности;

Х	х1	х2	х3	…..	хn
Р	р1	р2	р3	…..	рn

г

Рi

) графически (в виде многоугольника распределения).

Значение случайной величины, имеющее наибольшую вероятность, называется модой.

Так как события “x принимает значение x_i,” где i=, 2,…, n образуют полную систему, то

p+ р₂+ ….+р_n = 1.

Основные законы распределения дискретных случайных величин. А. Биномиальное распределение.

Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность наступления А в каждом испытании постоянна и равна р, а не наступления q.

Закон распределения случайной величины. Х - “ числа появлений события А в этих испытаниях” имеет вид:

Х	0	1	2	3	…	k	…	n
Р	Pn	Pn(1)	Pn(2)	Pn(3)	…	Pn(k)=Cnkpkqn-k	…	Pn(n)

Биномиальным называют распределение вероятностей, определяемое формулой Бернулли. Биномиальное распределение широко применяется для исследования дискретных случайных величин, встречающихся в теории надёжности.

По такому закону распределена случайная величина “ число отказов, возникающих в процессе проведения однотипных независимых испытаний выборки изделий”, при условии, что равновероятно появление отказа в любом из проводимых испытаний случайной выборки изделий данного типа.

Введем обозначения:

р – вероятность появления отказа в каждом испытании (р = const),

n - число испытаний;

m – возможное число появлений отказов при n испытаниях

(0 ≤ m ≤ n).

Тогда вероятность того, что в n независимых испытаниях произойдет ровно m отказов, вычисляется по формуле Бернулли:

Рn(т) =

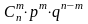
где т=0,1,2,…, п;

В. Распределение Пуассона.

При очень малых значениях вероятности р, достаточно больших п биномиальное распределение может быть заменено распределением Пуассона. Сделаем также допущение, что nр = а =const. Это означает, что среднее число появлений события в различных сериях испытаний, т.е. при различных значениях n, остается неизменным. Тогда вероятность того, что в n независимых испытаниях событие появится ровно т раз, вычисляется по формуле

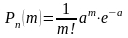
где а =nр;

n - число всех испытаний;

р – вероятность появления события в каждом испытании.

Распределение Пуассона, или “закон редких явлений”, применяется для определения вероятности отказа или отбраковки m изделий из выборки, содержащей n однотипных изделий (при указанных ограничениях, накладываемых на n и р, а именно, при р ≤ 0,1).

На практике часто применяется следующий критерий правильности предположения о наличии пуассоновского распределения дискретной случайной величины: если статистические оценки математического ожидания и дисперсии случайной величины близки по значению, то случайная величина распределена по закону Пуассона.