теория вероятностей

Случайные события

§ I. Непосредственное вычисление вероятности

Если опыт сводится к системе случаев, то вероятность события А равна отношению числа исходов, благоприятствующих этому событию, к общему числу всех единственно возможных, несовместных и равновозможных исходов:

,

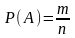где p(A) – вероятность события A;

m – число исходов, благоприятствующих событию А;

n –общее число всех единственно возможных, несовместных и равновозможных исходов.

Вероятность достоверного события равна I.

Вероятность невозможного события равна 0.

Вероятность случайного события есть положительное число, заключенное между нулём и единицей.

Итак, для любого события А выполняется условие:

0 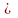p(A) 1

§ 2. Теоремы сложения и умножения вероятностей

Определение 1. Суммой (объединением) двух событий А и В называется третье событие С, состоящее в появлении или события А, или события В, или обоих этих событий.

С=А + В или С= А В.

Определение1^/. Суммой нескольких событий называется событие, состоящие в появлении хотя бы одного из этих событий.

Определение 2. Произведением ( пересечением) двух событий А и В называется такое третье событие С, которое состоит в совместном появлении и события А, и события В.

С= А ^. В или С = А В.

Определение 2^/. Произведением нескольких событий называется событие, состоящее в совместном появлении всех этих событий.

Теорема сложения вероятностей Для совместных событий а и в

р( А + В )= р(А) + р(В) – р(АВ).

Следствие 1.Если события А и В несовместные, то

р( А + В )= р(А) + р(В).

Следствие 2.Если события А₁, А₂…,А_n попарно несовместные, то р(А₁+А₂+……+А_n) =р(А₁)+р(А₂)+……..+р(А_n).

Теорема умножения вероятностей

Теорема1. Вероятность совместного наступления (произведения) двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило.

р(А В)= р(А) ^. р_А(В).

Следствие. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий.

р( А В )= р(А) ^. р(В).

Теорема 2. Вероятность произведения нескольких событий равна произведению вероятностей этих событий, причём вероятность каждого последующего по порядку события вычисляется при условии, что все предыдущие уже произошли.

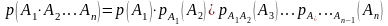
Определение. События называются независимыми в совокупности, если каждое из них и любое произведение остальных (включающее либо все остальные события, либо часть из них) есть события независимые. События независимые в совокупности, очевидно, попарно независимы между собой; обратное неверно. Таким образом, требование независимости в совокупности сильнее попарной независимости.

С л е д с т в и е. Вероятность произведения конечного числа независимых в совокупности событий равна произведению вероятностей этих событий.

р(А₁ ^. А₂ ^. ……^. А_n) =р(А₁) ^. р(А₂) ^.….^. р (А_п).

§ 3. Вероятность появления хотя бы одного события

Пусть в результате испытания могут появиться n событий А₁, А₂,……, Аn, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причём известны вероятности р(А₁), р(А₂),……,р(Аn) появления каждого из этих событий. Тогда вероятность того, что наступит хотя бы одно из этих событий, вычисляется по формуле:

Р(А) = 1 - р(В₁) × р(В₂) ×……× р(Вn),

Где Вi (i = 1,2, …… n) - события, противоположные Аi .

Если, в частности, р(А₁) = р(А₂) =……= р(Аn) = р, то вероятность появления хотя бы одного из событий А₁, А₂,……, Аn вычисляется по формуле

р(А) = 1 – qⁿ,

где q = 1 – р.