Межсимвольная зависимость

При более вдумчивом рассмотрении текста можно заметить, что существует некоторая зависимость между соседними символами осмысленного текста.

Например, в русском языке после гласной буквы не может стоять «ъ» или «ь»; после шипящих не могут стоять «я» или «ю»; после нескольких согласных подряд увеличивается вероятность гласной и т.д.

В английском языке буква «h» имеет большую вероятность встретиться, если «t» была предыдущей буквой, чем если бы «d» была предыдущей.

Такая межсимвольная зависимость должна учитываться в точной мере энтропии. Как правило, межсимвольная зависимость сокращает энтропию, и это означает, что могут быть построены коды с более короткими средними значениями длины слова. Действительно, эта идея является основой многих современных методов сжатия.

Мы знаем, что при объединении зависимых источников, суммарная энтропия меньше суммы энтропий отдельных источников (H(S,T) ≤ H(S) + H(T); следовательно, информация, передаваемая отрезком связанного текста, всегда меньше, чем информация на один символ, умноженная на число символов. С учётом этого обстоятельства более экономный код можно построить, если кодировать не каждую букву в отдельности, а целые «блоки» из букв. Например, в русском тексте имеет смысл кодировать целиком некоторые часто встречающиеся комбинации букв, как «тся», «ает», «ние» и т.п. Кодируемые блоки располагаются в порядке убывания частот, как буквы в табл. 1, а двоичное кодирование осуществляется по тому же принципу.

В ряде случаев оказывается разумным кодировать даже не блоки из букв, а целые осмысленные куски текста. Например, для разгрузки средств связи в предпраздничные дни целесообразно кодировать условными номерами целые стандартные тексты, вроде «поздравляю новым годом желаю здоровья успехов работе».

В любом телефоне при выборе языка предлагают воспользоваться упрощённым вариантом, который даёт возможность вставлять целые блоки текста в смс.

Вероятности в английском языке

Актуальной является задача эффективного кодирования английского текста для сжатия текстовых документов. Для прогнозирования возможного преимущества при сжатии необходима оценка фактической энтропии английского языка с учётом межсимвольной зависимости.

Для удобства часто принимается допущение, что алфавит состоит всего лишь из 26 символов (26 букв и пробел или пунктуация). Поскольку 2⁵=32, все 27 символов могут быть закодированы с помощью двоичного блок-кода, при котором каждое слово имеет длину 5. Однако, 27 – это меньше 32, поэтому фактическая энтропия меньше пяти битов.

Простейшая оценка энтропии английского языка (оценка нулевого порядка) основываются на допущении, что все буквы алфавита являются равно вероятными с вероятностью 1/27. Соответствующая энтропия нулевого порядка, обозначаемая H₀, поэтому равна H₀ = log27 = 4,755 бита на букву текста. Это верхний предел, поскольку, если вероятности не будут одинаковыми, энтропия уменьшится. Однако этот предел является важной точкой отсчёта.

Вероятности букв алфавита, т.е как часто они встречаются в английском тексте, различны. Более того этот показатель меняется в зависимости от типа документов.

Таблица 4 Вероятности встречаемости букв английского алфавита

A	0,064	N		0,056
B	0,014	O		0,056
C	0,027	P		0,017
D	0,035	Q		0,004
E	0,100	R		0,049
F	0,020	S		0,056
G	0,014	T		0,071
H	0,042	U		0,031
I	0,063	V		0,010
J	0,003	W		0,018
K	0,006	X		0,003
L	0,035	Y		0,018
M	0,020	Z		0,002
Пробел/пунктуация			0,166

Энтропия английского языка на основе вероятностей букв называется оценкой первого порядка и обозначается H_1. На основании данных, приведённых в таблице 4, можно вычислить, что H₁=4,194, что является скромным уменьшением энтропии по сравнению со случаем одинаковых значений вероятности. Исходя из этой оценки, предполагается, что код Хаффмена для алфавита будет иметь среднюю длину ближе к 4, чем к 5.

Кодирование по алгоритму Хаффмена, действительно используется в качестве метода компрессии английского текста, и, как предполагается, документы требуют приблизительно на 20% меньше памяти, чем в случае использования стандартного кода ASCII.

Если идти дальше и рассматривать частотность пар букв. Согласно расчётам вероятности пар составляют 27²=729, и эти вероятности означают энтропию H₂ (на одну букву, не на одну пару), равную приблизительно 3,3.

Если далее рассматривать вероятность (частотность) троек букв, то 27³=19683 троек, то получится значение энтропии H_3, которая приблизительно равна 3,1 бит. Шеннон сумел приблизительно оценить H₅  2,1 бит, H₈  1,9 бит. Аналогичные исследования для русского языка дают H₂^(r)=3,52 бит; H₃^(r)=3,01 бит.

Эти данные дают оценки значения средней информации на один знак при существующей зависимости рядом стоящих букв I_0, I_1, I₂ …

Сообщения (а также источники, их порождающие), в которых существуют статистические связи (корреляции) между знаками или их сочетаниями, называются сообщениями (источниками) с памятью или марковскими сообщениями (источниками)

Распространим эту мысль на бесконечное число корреляций. Тогда можно оценить предельную информацию на один знак в конкретном языке I_, которая будет отражать минимальную неопределённость, связанную с выбором знака алфавита без учёта семантических особенностей языка. I₀ вычисляется без учёта зависимости между буквами и характеризует наибольшую информацию, которая может содержаться в знаке данного алфавита. Шеннон ввёл величину, которую назвал относительной избыточностью языка:

По аналогии с величиной R, характеризующей избыточность языка, можно ввести относительную избыточность кода (Q):

Если исходное сообщение содержит I^(A) информации, а закодированное - I^(B), то относительная избыточность кода (Q):

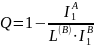
где – средняя длина кода (кодовых слов).

В случае двоичного кодирования формула приобретает вид:

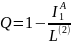
где – средняя длина двоичного кода (двоичных кодовых слов).

Избыточность является мерой бесполезно совершаемых альтернативных выборов при чтении текста. Эта величина показывает, какую долю лишней информации содержат тексты данного языка; лишней в том отношении, что она определяется структурой самого языка и, следовательно, может быть восстановлена без явного указания в буквенном виде.

Исследования Шеннона для английского языка дали значение I_1,41,5 бит, что по отношению к I₀=4,755 бит создаёт избыточность около 0,68. Подобные оценки показывают, что и для других европейских языков, в том числе русского, избыточность составляет 60 – 70 %. Это означает, что в принципе возможно почти трёхкратное (!) сокращение текстов без ущерба для их содержательной стороны и выразительности. Именно избыточность языка позволяет легко восстановить текст, даже если он содержит большое число ошибок или неполон.

Алфавитное неравномерное кодирование

Двоичное неравномерное кодирование с использованием разделителей

Возможны различные варианты двоичного кодирования, однако не все они будут пригодны для практического использования – важно, чтобы закодированное сообщение могло быть однозначно декадировано, т.е. чтобы в последовательности 0 и 1, которая представляет собой многобуквенное кодированное сообщение, всегда можно было бы различить обозначения отдельных букв. Проще всего этого достичь, если коды будут разграничены разделителем – некоторой постоянной комбинацией двоичных знаков.

Условимся, что разделителем отдельных кодов букв будет последовательность 00 (признак конца знака), а разделителем слов – 000 (признак конца слова – пробел). Примем следующие правила построения кодов:

• код признака конца знака может быть включён в код буквы, поскольку не существует отдельно (т.е. коды всех букв будут заканчиваться на 00);

• коды букв не должны содержать двух и более нулей в середине (иначе они будут восприниматься как конец знака);

• код буквы (кроме пробела) всегда должен начинаться с 1;

• разделителю слов (000) всегда предшествует признак конца знака; при том реализуется последовательность 00000 (т.е. если в конце кода встречается комбинация …000 или …0000, они не воспринимаются как разделитель слов); следовательно, коды букв могут оканчиваться на 0 или 00 (до признака конца знака)

Пример:

Буква	Код	pi *103
пробел	000	174
о	100	90
е	1000	72
а	1100	62
и	10000	62

Двочное неравномерное кодирование без использования разделителей

Условие Фано:

Неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с началом (префиксом) какого-либо иного более длинного кода.

Например, если имеется код 110, то уже не могут использоваться колы 1, 11, 1101, 110101 и пр.

Если условие Фано выполняется, т при прочтении (расшифровке) закодированного сообщения путём сопоставления со списком кодов всегда можно точно указать, где заканчивается одно кодовое слово и начинается другое.

Рассмотрим пример:

Пусть имеется таблица префиксных кодов:

а	л	ь	з	у	ы
10	010	00	11	0110	0111

Требуется декодировать сообщение: 00100010000111010101110000110.

Декодирование производится циклическим повторением следующих действий.

1. Отрезать от текущего сообщения крайний левый символ, присоединить к рабочему кодовому слову.

2. Сравнить рабочее кодовое слово с кодовой таблицей; если совпадения нет, перейти к шагу 1.

3. Декодировать рабочее кодовое слово, очистить его.

4. Проверить, имеются ли ещё знаки в сообщении; если «да», перейти к шагу 1.

Применение этого алгоритма даёт:

Шаг	Рабочее слово	Текущее сообщение	Распознанный знак	Декодированное сообщение
0	пусто	00100010000111010101110000110	-	-
1	0	0100010000111010101110000110	нет
2	00	100010000111010101110000110	м	м
3	1	00010000111010101110000110	нет	м
4	10	0010000111010101110000110	а	ма
5	0	010000111010101110000110	нет	ма
6	00	10000111010101110000110	м	мам
…

Проведя процедуру до конца, получим сообщение: «мама мыла раму».

Таким образом, использование префиксного кодирования позволяет делать сообщение более коротким, поскольку нет необходимости передавать разделители знаков.

Однако условие Фано не устанавливает способа формирования префиксного кода и, в частности, наилучшего из возможных.

Способ оптимального префиксного двоичного кодирования был предложен Д. Хаффманом. Метод Хаффмана и его модификация – метод адаптивного кодирования (динамическое кодирование Хаффмана) - нашли широчайшее применение в программах-архиваторах, программах резервного копирования файлов и дисков, в сисиемах сжатия информации в модемах и факсах.

Теоретически имеется огромная возможность для сжатия текста (для английского текста – 67 %). Текстовый файл может быть теоретически быть сжат до размера, составляющего одну треть от первоначального. Однако, чтобы достигнуть этих результатов необходимо использовать сложный процесс кодирования и декодирования. Само по себе кодирование по алгоритму Хаффмана не позволит нам продвинуться значительно вперёд, поскольку даже кодирование 27² =729 пар букв даёт нам всего лишь скромную компрессию по сравнению с тем, что возможно теоретически.

Кодирование Лемпеля – Зива

Опубликован в 1977 году. Метод основывается на на том, что последовательности букв в английском тексте не являются полностью случайными, а время от времени повторяют образцы. Эти образцы составляют слова или даже фразы. Метод Лемпеля-Зива, в сущности, создаёт словарь этих общепринятых образцов.

Метод имеет глубокие теоретические основания и практика доказала его мощность. Можно доказать, что в своём идеальном виде этот метод создаёт в пределах длинного текста коэффициент компрессии, равный коэффициенту, прогнозируемому энтропией текста. Поэтому он является универсальным алгоритмом компрессии, основанным на простой схеме записи.

В методе Лемпеля-Зива и отправитель, и получатель ведут запись того, что уже было отправлено. Затем при подготовке к отправке дополнительного текста отправитель снова смотрит на ранее переданный текст, для того, чтобы найти дублирование максимальной длины того, что требуется отправить дальше. После этого вместо самой последовательности отправляется ссылка на прошлую дублирующую последовательность. Например, если предстоит отправить слово, которое передавалось ранее, отправитель просто отправляет ссылку на позицию этого слова в прошлом.

В идеальном случае вся история ранее переданного текста сохраняеся как отправителем, так и получателем, но на практике запоминаемая история ограничивается размером памяти для её хранения (буфер упреждающей выборки). а значит и длина отправляемой последовательности тоже ограничена буфером упреждающей выборки.

Ссылка на прошлую последовательность передаётся путём отправки тройки (x, y, z), где

x – число позиций в обратном направлении в буфере, где начинается дублируемая последовательность символов.

y – количество символов для дублирования (копирования).

z – следующая буква (символ) в упреждающей выборке после скопированных.

Например:

Свиристель свиристит свирелью

x	y	z	добавляемая последова тельность	Буфер поиска	Буфер упреждающей выборки
0	0	с	с		свиристель-свиристит-свирелью
0	0	в	в	с	виристель-свиристит-свирелью
0	0	и	и	св	иристель-свиристит-свирелью
0	0	р	р	сви	ристель-свиристит-свирелью
2	1	с	ис	свир	истель-свиристит-свирелью
0	0	т	т	свирис	тель-свиристит-свирелью
0	0	е	е	свирист	ель-свиристит-свирелью
0	0	л	л	свиристе	ль-свиристит-свирелью
0	0	ь	ь	свиристел	ь-свиристит-свирелью
0	0	-	-	свиристель	-свиристит-свирелью
11	7	и	свиристи	свиристель-свиристи	т-свирелью
2	1	-	т-	свиристель-свиристит-	свирелью
10	4	е	свир	свиристель-свиристит-свир	елью
18	3	ю	елью	свиристель=свиристит=свирелью

При использовании процедуры Лемпеля-Зива нужно поддерживать определённый компромисс между размером буферов (которые пользуются памятью и требуют времени поиска и обработки) и эффективностью процедуры с точки зрения образцов, на которые может даваться ссылка. Другое соображение касается отправки тройки (x, y, z). В случае больших буферов и x и y принимают значения в большом диапазоне и отсюда моут потребовать большого числа битов для передачи.

Несколько популярных алгоритмов компрессии, которые можно найти на персональных компьютерах, включая ZIP, PKSip, LHarc, PNG, gzip, ARJ, основаны на методе Лемпеля-Зива LZ77 вместе с компрессионным кодированием ссылочной информации. Эти пакеты достигают хороших коэффициентов сжатия.