Зависимость от динамических характеристик измеряемой величины

В соответствии со сложившейся классификацией большинство авторов при рассмотрении динамических процессов, связанных с изменениями самой измеряемой величины и переходными режимами в СИ, выделяют два вида погрешностей: статические и динамические. Статическими называют погрешности измерения постоянных величин. Погрешность в динамическом режиме, т. е. при измерении изменяющейся величины, полагают равной сумме статической и собственно динамической погрешности. Таким образом, динамическую погрешность определяют как разность погрешности в динамическом режиме и статической погрешности СИ.

Существуют два принципиально различных вида СИ: аналоговые (измерительные преобразователи, измерительные приборы с электромеханическими измерительными механизмами) и цифровые (АЦП, цифровые измерительные приборы). Аналоговые СИ работают в следящем режиме, поэтому для оценки динамических свойств можно использовать частотные характеристики, все виды переходных функций. Цифровые СИ функционируют в дискретном времени. Относительно момента пуска результат на выходе появляется через некоторый интервал времени, необходимый для реализации процесса сравнения. Величина этого интервала является временем чистого запаздывания между положением на временной оси измеряемого значения и моментом получения результата.

Аналоговые СИ. Моделью любого реального аналогового СИ является так называемая “динамическая система”, связь между координатами которой описывается линейным дифференциальным уравнением с постоянными коэффициентами вида

, (1.1)

где a_i , b_i – постоянные коэффициенты, x(t), y(t) – входная и выходная переменные, 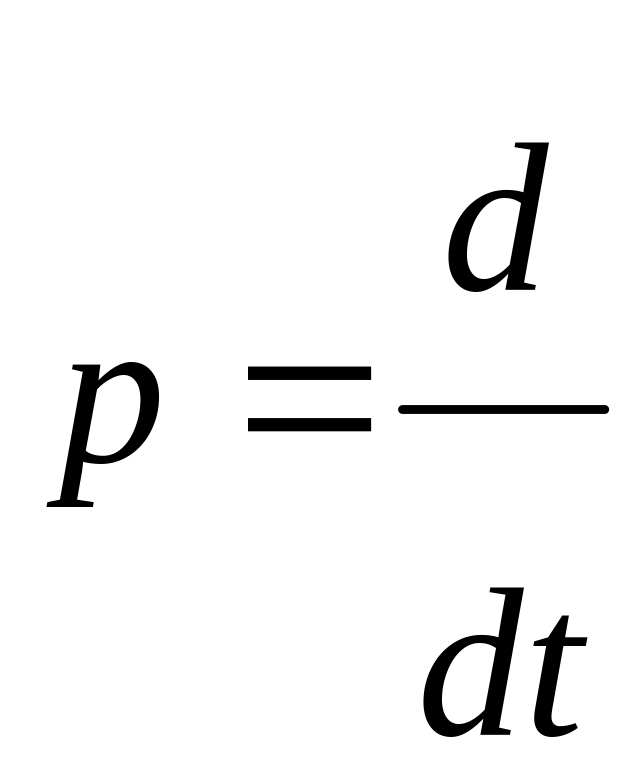– оператор дифференцирования.

Кроме дифференциального уравнения иногда используют передаточную функцию, частотную передаточную функцию. Оценкой динамических свойств таких устройств являются параметры реакции на стандартные входные сигналы: единичный скачок, дельта-функцию, гармоническое воздействие. К ним относятся время нарастания, время установления, амплитуда и фаза выходного сигнала. Для аналоговых СИ воздействия типа 1(t) возникают при скачкообразных изменениях входных сигналов или в режиме коммутации. Переходные функции удобно использовать для оценки динамических свойств СИ, а не динамических погрешностей, так как в реальных объектах измерения нет ограничений на форму кривой изменения физических переменных. Наиболее общей моделью, описывающей меняющееся входное воздействие аналогового СИ, является нестационарный случайный процесс.

Динамическая погрешность СИ, представленного уравнением (1.1), при входном сигнале произвольной формы есть разность

,

где y(t) – решение уравнения (1.1) для конкретного вида x(t).

Известно, что общий интеграл линейного дифференциального уравнения (1.1) равен сумме частного решения неоднородного уравнения и полного решения однородного уравнения. Частное решение неоднородного дифференциального уравнения есть вынужденная составляющая y_в(t) выходного сигнала y(t). Однородное уравнение получается из исходного, если в нем положить правую часть равной нулю. Его решение y_с(t) – свободная составляющая y(t). Любое свободное решение можно представить в виде суммы экспоненциальных слагаемых, число которых равно числу корней характеристического уравнения

.

Таким образом, значение выхода y(t)=y_в(t)+y_с(t) при стремится к вынужденной составляющей (рис. 1.3,а).

Следовательно, динамическая погрешность для входного сигнала произвольной формы есть свободная составляющая решения уравнения (1.1) с противоположным знаком (рис. 1.3,б): .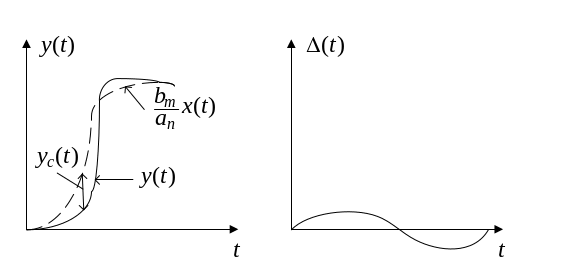

а б

Рис. 1.3. Динамическая погрешность

аналогового СИ

Ц

Рис. 1.4. Формирование

динамической погрешности

цифрового СИ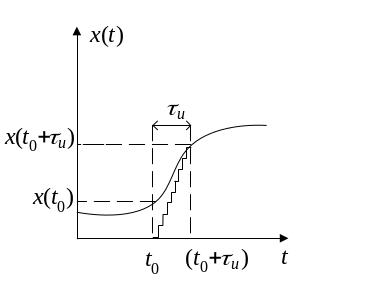

ифровые СИ. Для цифровых СИ не существует промежуточных значений выхода между моментом запуска и получением результата, поэтому основной характеристикой динамических свойств является время измерения τ_и. При изменяющемся входном сигнале x(t) возникает динамическая погрешность, так как за время от момента пуска t₀ до момента окончания процесса сравнения t₀+ τ_u входная величина успе-вает измениться от значения x(t₀) до x(t₀+τ_u) (рис. 1.4).

На выходе СИ появляется результат , и динамическая погрешность равна , если статической погрешностью пренебречь. Оценим величину этой погрешности для входного сигнала произвольной формы.

Предположим, что функция x(t) является непрерывной и дифференцируемой на интервале наблюдения. Ее разложение в ряд Тейлора в окрестностях точки t₀ имеет вид

. (1.2)

Продифференцировав ряд (1.2) n раз, выразим коэффициенты полинома через значения производных в точке t₀

. (1.3)

Подставив в разложение (1.2) t = t₀+τ_u , найдем динамическую погрешность ∆(t) как разность x(t₀+τ_u) и x(t₀)

. (1.4)

Линеаризовав функцию (1.4) путем отбрасывания всех членов ряда, кроме первого, получим оценку динамической погрешности

.

Таким образом, динамическая погрешность цифровых СИ в первом приближении зависит как от скорости изменения измеряемой физической величины, так и от времени измерения.