1.Числовые множества.Ограниченность,точные грани.

Множество X наз.ограниченым если некоторые фиксированые М: <М; x

В противном случае такое условие X не выполняется то множество наз. неограниченным X наз. ограниченым сверху М: <М, X наз. ограниченым снизу если m: x>m

Числа М и m из посл.двух опред. наз. соответственно верхней и нижней гранью множества.

Ограниченое множество явл.ограниченым сверху и снизу Х-огранич.сверчу множество наименьшая из всех верхних граней этого множества наз.точкой верхней гранью множ.Х

2.Числовые последовательности.Предел числовой последовательности.

Если каждому поставлено R то говорят что задана числовая последов.

, ,...,

Число а наз.пределом посл. если для n : < V

Последовательность,иьеющая конечный предел,наз.сходящаяся.Если последовательность не имеет предела-расчодящая.

3. Необходимый признак сходности числ.посл.(Теорема):

Если { } сходится,то она ограничена.

Док-во:

Воспользуемся определением сходимости обозначив через ;по определению: < ,

Замечания: 1.

а) в обратную сторону не утверждение действует

б) если последовательность ограничена,то она не обязательно сходиться.

4. Теорема о переходе к пределу в неравенстве:

Пусть и ; ,Тогда Док-во: предложим противное: > < ;по определению пределов:

(*) <

(**) <

будут выполнены (*) и (**)

< < < < ;т.е

< ,что противоречит условию значит < не верно,а -верно(утверждение теоремы);

если в условии теоремы записать,что < ; то

<

>

=

4. Теорема о 2-х милиционерах:

Пусть и : ;

Док-во:

Пусть >0 тогда по опр.пред:

(*) < ;

(**) < ;

тогда вып (*) и (**)

т.е

5.Арифметические операции над сходящимися послед.

-2 послед., -нек. числа

; ; ;

6.Достаточный признак сходимости числовых посл.

Если последовательность ограниченая и монотонная то она сходится.

Пусть а=sup По определению supremum,если

: a- <

Для определенности рассматриваем неубывающую послед.

Поскольку монотонная неубывающая послед.

т.к.

т.е. <

7. число : числом наз. предел

число Неппера

явл. трансцендентным

8.Принцип вложенных отрезков.

Пусть заданна с-ма влож.отрезков :

Причём =0

Тогда единственная т.

неубывающвя и ограничена пусть невозрастающая и ограничена.

иначе нарушается >

9.Подпоследовательности.Теорема Больцано—Вейерштрасса.

Опр. Дана если рассмотреть послед-ть,кот-я состоит из таких ? членов но не всех,причём порядок следования сохраняетсяется ,то такая посл-ть наз.подпоследовательностью последовательности

Замечание:

---Если посл-ть то и всякая её подпосл-ть также сходится к

---Расходящаяся посл-ть может иметь счодящиеся подпосл-ти

Теорема Больцано—Вейерштрасса.

Из всякой ограниченой посл-ти можно извлечь сходящуюся подпосл-ть.

Док-во:

Поскольку все члены посл-ти ограничены то точки max на отрезке.

выборочный член

разделим напополам и обозначим через ту часть,которая содержит бесконечно много членов то найдена : .Разделим напополам и выберем -содержащий бесконечно много членов

продолжим до в результате получим члены этой посл-ти max внутри с-мы.

10. Верхний и нижний пределы последовательностей:

, -предельная точка этой последовательности если существует подпосл-сть

Верхним пределом последовательности наз. наибольшая из предельных точек данной последовательности.

Нижним пределом наз. наименьшая из предельных точек

-верхний предел

-нижний предел

11.Фундаментальныепоследовательности, критерий сходимости Коши:

наз. фундаментальной если > : <

Теорема: Критерий сходимости Коши:

Последовательность сходиться т.и.т.т., к. она фундаментальная; Без док-ва.

13. Различные опред. предела:

a)по Гейне число наз. пределом при

если такое,что

b)по Коши:

число наз пределом ф-ии при

если > > т. что < < <

НЕ ПОЛНОСТЬЮ!!!

15.Первый замечательный предел:

;док-во:

-четная ф-ия

>0

Без понятного рисунка

< <

< <

;

след:

16.2-ой земечат. предел:

;док-во:

Аналогично: ;знач: ;при

доказано,что

Пусть ;

знач. ;соответственно:

;

17. Бесконечно малые и беск. Большие ф-ии.

-Б.М. при если:

-Б.Б. если

Свойства:

1. ББ при -БМ при

2. Сумма(призведение) БМ ф-ий явл БМ ф-ей для ББ ф-ий

то же самое

3.если -ББ при и огран. в ,то

- БМ при

Ассимтотич. оценки:

Пусть и - БМ ф-ии при

Если

То ф-ии и наз. бесконечно малыми одного порядка:

если ,то ф-ии наз. эквивалентными при

если то говорят -БМ более высокого порядка чем :

если ; ,то говорят:

что-то там на счет к-ого порядка.

Теорема о пределе отношений БМ ф-ий.

18.Свойства эквивалентных бесконечно малых функций.

~

;

19.Определение непрерывности функции.Непрерывность слева и справа. Класификация точек разрыва.

Опрю непрер. непрерывна в

Если в этих опред. предел заменить на предел (справа),то получим определитель слева на непрерывности ф-ии слева (справа) из свойств пределов следует что ф-ия непрерывна в точке она непрерывна слева и справав этой точке. Если ф-ия непрерывна в то она наз.непрерывной на X.

Устранимые точки разрыва

т. нвз.устранимой точкой разрыва для если или не существует

Пределы слева и справа различны

-конечная наз.скачком разрыва

Разрыв 2-ого рода точка разрыва 2-ого рода

Если хотя бы один из одного предедов пределов при равен

20. Св-ва непрерывных ф-ций:в в отрезке:

1. Если ф-ция y=f(x) непрерывна на [a,b] и f(a)*f(b)<0, т.е. знаки f(a) и f(b) противоположны, то на (a,b) найдется хотя бы одна точка х=с, что f(c)=0 (график)-теорема Больцана-Коши.

2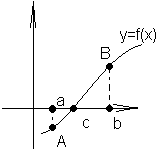 . Если ф-ция y=f(x) непрерывна на [a,b], то она ограничена на этом промежутке.

3. Если ф-ция y=f(x) непрерывна на [a,b], то она достигает на этом отрезке min m и max M (теорема Вейерштрасса).

в точке:

1. если ф-ция f(x) и g(x) непрерывна в х₀, то их сумма, произведение, частное (при (х₀)0) явл. ф-циями, непрерывными в х₀

2. если ф-ция y=f(x) непрерывна в х₀, и f(x₀)>0, то существует окрестность х₀, в которой f(x)>0

3. если y=f(U) непрерывна в U₀, а U=(x) непрерывна в U₀=(x₀), то сложная ф-ция y=f[(x)] непрерывна в х₀.

21 Обратн. Ф-ия.

Если задано правило, по которому каждому значению yY ставится в соответствие  ед. знач. х, причем y=f(x), то в этом случае говорят, что на мн-ве Y определена ф-ция обратная ф-ции f(x) и обозначают такую ф-цию x=f^-

1(y).

Непрерывность обратной ф-ции

Пусть у=f(x) – непрерывна при х [a,b] у[A,B] и пусть она строго возрастает, тогда ф-ция x=(y) также непрерывна {Д} Пусть y0[A,B]  x0=(y0), f(x0)=y0 x0(a,b) ; возьмём >0 столь малое, что [x0-,x0+][a,b] Пусть y1=f(x0-) y2=f(x0+) Тогда в силу строго возрастания ф-ции f y(y1,y2)x=(y)(x0-,x0+) тогда для у из [A,B] получаем [a,b]  мы получили на нём >0 удовлетв этому условию мы не взяли существ окрестность в (.) 0 (у1,у2) | у(у1,у2) соответсвует (y)(x0-;x0+) Если это утверждение справедливо для мал  то оно справедливо для +  ф-ция  - непрерывна в т. н0 по определению. {} Пусть у0=В  х0=(y0)=b Возьмём <b-a Пусть y1=f(x0-) тогда в силу строгого возрастания ф-ции f y(y,y0]  x=(y) при отображении  пойдёт в а (x0-,x0)  ф-ция  непрерывна в (.) у0 по определению. аналогично рассматривается случай с убыванием

22.Непрерывность элементарных ф-ций

1)f(x)=C –непрерывна на всей числовой прямой. f(x)=f(x+h)-f(x)=C-C=0; lim_h0f(x)=0;

2) f(x)=x; f(x)=x+h-x=h lim_h0h=0;

3)f(x)=xⁿ, nN –непрерывна на всей числовой прямой, непрерывна как произведение непрерывных ф-ций  по индукции xⁿ=x^n-1x;

4)f(x)=a0xⁿ+a1x^n-1+…+an-непрерывная на всей числовой прямой как сумма конечного числа непрерывных ф-ций;

5)R(x)=P(x)/Q(x)=(a0xⁿ+a1x^n-1+…+an)/(b0x^m+b1x^m-1+..+b^m)-непрерывна на всей числовой прямой за исключением тех х, при которых значение знам. обращ в 0 как частное двух непрерывных ф-ций.;

6) f(x)=sinx Лемма xR, |sinx|<=|x| Рассмотрим еденичную окружность.(OB,ox)=x; (OB’,ox)=x 0<=x<=/2 т.к. длина отрезка соед две точки не превосходит длины дуги окружности соединяющей теже точки  |BB’|<=BAB’ ; |BB’|=2Rsinx; BAB’{дуг}=2Rx  2Rsinx<=2rx; sinx<=x ; Если -/2<=x<0 то |sinx|=-sinx=sin(-x)<=-x=|x| ; 0<-x<=/2 Если |x|>/2  |sinx|<=1</2<|x| {док} что sinx- непрерывна. |f(x)|=|sin(x+h)-sinx|=|2sinh/2cos(x+h/2)|<=2|sinh/2| lim_h0sinh/2=0

7)f(x)=cosx – непрерывна на всей числовой прямой |f(x)|=|cos|x+h|-cosx|=(2sinh/2sin(x+h/2)<=2|h/2| |h|0;

8)f(x)=a^{x –}непр на всей числ пр,a>=0 f=(a^x+h-a^x)=a^x(a^h-1) lim_h0a^x(a^h-1)=0;

9)f(x)=log_ax a>0 a1 непрерывна на (0,+) 10)arcsinx, arccosx – на всей числ. пр.