
- •1.Қатты дене
- •2. Сұйық дене
- •3.Газ тәрізді дене
- •1.2. Механикалық кернеуден болатын деформация
- •1.3. Деформациялану жылдамдығы, ротор.
- •1.4. Механиканың бірыңғай ортасы үшін жалпы заңдылықтар мен теңдеулер
- •1.5 Тұтас орта термодинамикасының заңдары.
- •1.6 Гипстің тепе- теңдігі және диссипоция теңсіздігі
- •1.7 Онзагер принципі
- •1.8. Еркін (бос) энергия, энтальпия, Гиббстің термодинамикалық потенциалы
- •1.9. Тұтас ортаның кейбір математикалық моделі (үлгісі)
- •1.11. Ашық жүйелердің термодинамикасы
- •2.1. Адамның қарқынды қозғалмалы жүйесінің құрылымы
- •2. 5 Сурет. Бас сүйек жазықтығының сагиттальды иінтірегі [5]
- •2. 6 Сурет. Табан мен оған әсер ететін күштер бейнеленген.
- •2. 6 Сурет. Аяқтың ұшымен тұру [5]
- •2. 7 Сурет. Білек пен оған әсер ететін күштер бейнеленген.
- •2. 7 Сурет. Білек сүйектері, тіректі ұстап тұруы
- •2.2. Жердің ауырлық даласында екі аяқпен жүру кезінде дене массасының қозғалыс орталығы
- •2.8 Сурет. Масса орталығының бір қадамға өзгергендегі жүрген жолы
- •2. 3. Дөңгелек жүріс кезінде аяқтардың динамикасын теңестіру, қозғалыстың кезеңдері бойынша талдау
- •2.9 Сурет. Екі аяқты жүйенің моделі
- •2.4 Тұрақты әрекетсіз циркуль жүрісіне сипаттама
- •2.5 Бір периодтық жүріс кезіндегі төзімділік параметірлерін анықтау
- •2.14. Негізгі жалпы теория негізіндегі жүйенің биомеханикалық қозғалысы тепе-теңдікті қалыптастыру
- •2.15. Қозғалыс теңдеуін құратын көпзвеналық динамикалық жүйенің Лагранж формализмін қолдана отырып, деформацияланған элементтер құрылымы
- •2.16. Биомеханикалық бұрандама қозғалыс жүйесі бар, деформацияланған элемент құрылысының теңдеуі мен моделі
- •2.27 Сурет. Жазық қозғалысының бұрандама механикалық жүйесі мен бір тірек фазадағы өзгертілетін геометриялық буын моделі
- •2.17. Механикалық жүйелер элементтердің серпімді модулін анықтау
2. 3. Дөңгелек жүріс кезінде аяқтардың динамикасын теңестіру, қозғалыстың кезеңдері бойынша талдау
Пассивті дөңгелек жүрістің негізгі анықтамалары мен жобалау болжамдары. Дөңгелек жүріс- екі аяқты қозғалыстың ең қарапайым моделі.Бұл моделде аяқтар қатты болады, олардың тізелері мен өкшелері болмайды, бір- біріне топса арқылы қосылған. Қозғалыс екі өлшемді болады. Аяқтың жүретін жолының нүтелерімен қосылуы сұр доға ретінде болады, олардың орталықтары жермен байланысады, радиусы аяқтың ұзындығына сәйкес келеді. Қозғалысты жобалау 2.2 параграята қарастырылған.
Пассивті қозғалыс. Егер қадамдық жүйе ешқандай энергия көздерін қолданбаса, ондай қозғалыс жүйесін пассивті деп атайды. Динамика саласында ондай жүйелерді автономды деп атайды.
Орнықты жүріс. Бұл термин жүйенің ұзақ уақыт үздіксіз , құламай жүре алатынын білдіреді.
Жүріс қадамы аяқтың жерге тию және көтерілу мерзімін сипаттайды. 1 с ішінде неше рет қадам жасалғандығы, олардың ара- қатынасы өлшенеді.
Симметриялық жүріс. Егер әрбір екі қадам бірдей болса, ондай жүрісті симметриялы деп атайды. Әрбір қадамда уақыт- кеңістік сипаттамасы қайталанып отырады.
Екі буыннан құралған, екі аяқты қадамдық жүйенің дөңгелек жүрісіне қарапайым мысал келтірейік(2.9 сурет).
Екі аяқты дөңгелек жүрісті жобалағанда қолданылатын болжамдар.
Масса үш нүктеде жинақталады:
Топсаның массасы mH;
Әр аяқтың массасы m, a мен b ара- қашықтығында топса мен аяқ соңында орналасқан.
Жүйенің толық массасы MC=2m+ mH тұрақты, осы кезде массалардың қатынасы сынақ кезінде өзгеруі мүмкінµ= mH / m.
2.9 Сурет. Екі аяқты жүйенің моделі
Аяқтар бірдей. Аяқ ұзындығы L= a+ b тұрақты, бірақ ұзындықтар қатынасы β=b/a сынақ кезінде 0,1 мен 10 арасында өзгеруі мүмкін.
Жетек. Жүйеге ішкі энергия енбейді.
Сырты. Жүйе φ бұрышпен, жазықтық бетімен төмен жылжиды .
Жүріс екі кезеңнен тұрады:
Ауысу: бұл кезеңде жүйе тірек аяғының жерге жанасқан жерінде айналады; көндігу деп аталатын екінші аяғы ілгері қарай жылжиды; тіреуші аяқ сырғанамайды; жүйе өзін баллистикалық екілік маятник ретінде ұстайды.
Аяқтың алмасуы: үдеріс тез іске асады, көндігу аяғы жерге тигенде тіреуші аяқ көтеріледі; жүйенің геометриялық құрылымы өзгермейді, тіреуші аяқтың да, көндңгу аяғының да кинематикалық моменттері өзгермейді.
Қақтығысу: көндіру аяғының жерге жанасуы ешбір сырғанаусыз,серпімсіз болады.
Призмалық буындар: тізесіз және табансыз жүйелер көндіру аяғына зиянын тигізеді. Бұл ақау призмалық тізе бұлшық еттерін аяқтың төменгі салмақсыз бөлігінде қолдану арқылы шешіледі. Екі аяқ та бірдей ұзындықта L болады.
Жүйенің динамикасына қорытынды жасамастан бұрын, бірнеше белгілеуді мысалға келтірейік.
Жанасушылық
кезінде жүйевертикальді және сәйкесінше
бос және тірек аяқтар арасындығы θns
,
θsбұрыштар
арқылы сипатталуы мүмкін. Демек, жүйе
жағдайы төрт параметрлермен сипатталады:
θns
,
θs,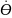 ns ,
s.
ns ,
s.
Аяқтарды ауыстыру кезінде жүйе α-аяқтар арасындағы жарты бұрыш және L адым ұзындығымен сипатталуы мүмкін, α және L келесі қатынаспен байланысқан L=2lsin α.
Жүйе қозғалған кезде , алдыға бағытталған оның орталық массаның жылдамдық компоненті (сыңары) ылғи өзгеріп отырады ұадам қозғалысы секілді.
Сондықтан біз циклдағы турасызықты қозғалыс аумағын анықтау үшін vәріпімен белгіленетін , алға қозғалу орта жылдамдық түсінігін енгіземіз.
2n
периодтық жүріс жағдайында v
– константа.
Егер n=0 яғни,жүріс бір периодты, v–ны
L/Tсияқты
есептеледі
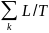 (Т-период шага). Улкен белгілер үшін n:
k-қадам счетчигі).Хаостық жүрісте
v-ныесептеу
мүмкін емес. Ол кезде v-ның
тек орта белгісі туралы айтуға болады.
(Т-период шага). Улкен белгілер үшін n:
k-қадам счетчигі).Хаостық жүрісте
v-ныесептеу
мүмкін емес. Ол кезде v-ның
тек орта белгісі туралы айтуға болады.
Тасмалдау кезеңі.
Аяқтар бірдей деп есептеледі,сондықтан кай аяқ тірек болып табылатынына қарамастантеңдік бірдей.Екінші түрдегі (рода) Лагранж тендеуін қолданып,динамикалық теңдік аламыз:
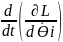 -
-
 = 0, (2,16)
= 0, (2,16)
Мұндағы, L-лагранж, ол өзімен потенциалдық және кинетиклық энергияның әр түрлілігін көрсетеді (L=Т-П).
Кинтикалық энергия үшін теңдік түрі [16-18]:
![]() (2,17)
(2,17)
Мұндағы,

![]()
Потенциалдық энергия үшін теңдік түрі:
![]() (2,18)
(2,18)
Кинетикалық энергия теңдігіне жылдамдық сипаттамасын қойсақ, келесіні аламыз:
T= 2ns mb2-2 ns smlb cos (θs -θns) + 2s (mH l2+m(l2+a2)).(2,19)
(2.19) формуладан П үшін теңдік шегріп және екінші түрдегі Лагранж теңдуін қойсақ, динамикалық жүйенің екі теңдеуін аламыз:
- Ӫns mlb cos (θs - θns) + 2ns mlb sin(θs - θns) + Ӫs (mH l2 +m (l2+a2)) + mH glsin θs -mga sin θns -mgl sin θns =0,(2,20)
- Ӫns mb2- Ӫs mlb cos (θs - θns)+ + 2s mlb sin(θs - θns)mgb sin θns =0
Бейсызықты дефференциалды теңдіктер жүйесі екінші тәртіпке ие. Оның аналиткалық дәл шешімін шешімін алу мүмкін емес. Аналитикалық шешімін алу үшін, бүрыштар нөлден аз айырмашылығы бар деп болжап,(2.20) теңдеуді сызықтандырамыз .
Сызықтандырамыз нәтижесінде теңдеулер жүйесін аламыз:
-Ӫns mlb+ Ӫs (mHl2+m(l2+a2))- mH glθs- mga θs- mgl θns=0,
- Ӫns mb2-Ӫs mlb-mgb sin Ӫns=0. (2,21)
Көрсетілген теңдіктер негізінеде жүріс үрдісінің сипаттамасы аяқтардың ұзындығы мен оның массасына байланысты емес, ал келісі қатынасқа μ=mH/m масса және β= b/aұзындық байланысты екені тағайындалған.
Аяқтарды ауыстыру кезеңдері.
Аяқтардың ауысуы кезінде ауыстырылатын аяғының жермен жанасуы және тірек аяғының жерден үзілуі болады,осы кезде ауыстырылатын аяғы тіреу аяғына айналады және керісінше.
Аяқтардың ауысуы кезінде жүйе жағдайы төрт параметрмен сипатталады:
Ө-s,Ө-ns– аяқтардың ауысуы алдыңдағы вертикальмен тірек және ауыстырылатын аяқтарының бұрышы;
-s, -ns – аяқтардың ауысуы алдыңдағы тірек және ауыстырылатын аяғының бұрыштық жылдамдығы;
Аяқтардың ауысқаннан кейін жүйе жағдайы төрт параметрмен сипатталады:
Ө+s,Ө+ns–аяқтардың ауысуқанан кейін вертикальмен тірек және ауыстыру аяқтарының бұрышы;
+s, +ns–аяқтардың ауысуқанан кейін тірек және ауыстыру аяғы бұрыштық жылдамдығы;
Аяқтардын ауысар алдындағы және ауысқаннан кейінгі бұрыштары келесі қатынаспен байланысты:
-s=Ө-ns;Ө+ns= -s;
Кинетикалық момент жүйесінің шартын сақтау арқылы аяқтардың ауысуын үрдісін сипаттайтын келесі теңдікті аламыз;
mh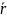 -h
-h
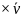 -h
+m(
-s
-s+
-ns
-ns)
=
mh
+h
+h
+m(
+s
+s+
+ns
+ns),
-h
+m(
-s
-s+
-ns
-ns)
=
mh
+h
+h
+m(
+s
+s+
+ns
+ns),
m -hs -s= m +hs +s,(2,22)
Мұнда векторлар аяқтардың ауысуына дейін жағдайды сипаттайды:
-h
=-l
sinӨ-ns
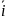 + l cos
Ө-ns
+ l cos
Ө-ns
 – жер мен тіреy емес аяқтын соңынан
топса (шарнир) (буын) дейінгі векторы;
– жер мен тіреy емес аяқтын соңынан
топса (шарнир) (буын) дейінгі векторы;
-s =(b sinӨ-s + l cos Ө-ns ) –тірек емес аяқтынсоңынан тірек аяғының ц.м.дейінгі векторы;
-ns =-a sinӨ-ns + a cos Ө-ns –тірек емес аяқтын соңынантірек емес аяғының ц.м.дейінгі векторы;
-ns =-b sinӨ-s + a cos Ө-ns –буын топсасынан тірек аяғының ц.м.дейінгі векторы;
Аяқтардын ауысуынан кейін жағдайды сипаттайтын векторлар:
+h =-l sinӨ+ns + l cos Ө+ns –жермен тірек аяқтын соңынан топса (шарнир) (буын) дейінгі векторы;
+s = (b sinӨ+s + l sin Ө+ns ) –тірек аяғытын соңынан тірек емес аяқтын ц.м.дейінгі векторы;
+ns =- a sinӨ+ns + a cos Ө+ns –– тірек аяқтын соңынан тірек аяғының ц.м.дейінгі векторы;
-hns = b sin Ө+ns + b cos Ө+ns –– – буын топсасынан тірек емес аяғының ц.м.дейінгі векторы;
Формулаға векторлар мен жылдамдықты қойсақ, аяқтардың ауысуы кезіндегі бұрыштық жылдамдық теңдеулер жүйесін аламыз:
+=
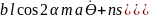 +
+
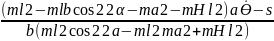 ,
,
+=
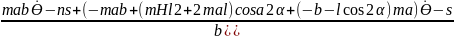 .
(2.23)
.
(2.23)
Жылдамдық теңднулерің шешу. (2.21) теңдеулер жүйесін ынғайлы түрге келтіреміз:
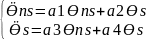 (2.24)
(2.24)
a1= ;
a2
;
a2 ;
(2.25)
;
(2.25)
a3=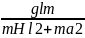 ;
a4=
;
a4=
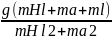 ;
;
(2.24) жүйесі дифференциалдық теңдеулер теориясының белгілі әдістерімен шешіледі.
